Wave sediment transport

1
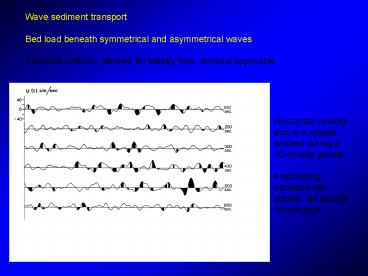
Wave sediment transport Bed load beneath
symmetrical and asymmetrical waves ? Shields
criterion, derived for steady flow, remains
applicable
Horizontal velocity above a rippled seabed during
a 10-minute period. ? oscillating transport
can appear as almost continuous
2
Instantaneous bed load transport ? empirical
transport rate formulae for steady flow may be
applied instant by instant through wave cycle ?
time-averaging results gives net sand transport
rate ? for symmetrical waves ? no net motion
3
? for asymmetrical waves, net onshore transport
is expected
4
Net bed load transport beneath steep Stokes 2nd
Order waves
Regions of validity for various wave theories H
wave height, h water depth T wave period g
accel. due to gravity Stokes 2nd-order theory
most usually applied in intermediate or
transitional water depth

• correction ?2 to linear wave profile ?1 of
  magnitude proportional to wave steepness (ak)

5
The near-bed velocity amplitude (first harmonic)
for a sinusoidal wave is given by
where a
H/2 amplitude of surface elevation The
corresponding peak Shields parameter during the
wave cycle is
Using Soulsbys (1997) friction factor
yields the peak Shields parameter (skin friction)
for a sine wave as
6
Beneath asymmetrical (Stokes 2nd Order) waves the
velocity, and hence bed shear stress, are
asymmetrical
The wave velocity may be expressed where the
asymmetry parameter W is given by
7
We now make the assumption of quasi-steadiness
with regard to the bed shear stress and assume
that the instantaneous Shields parameter is given
by
(Quadratic
friction)

• What is the net bed load sediment transport rate?
• Here we make an unsteady application of Soulsbys
  bed load formula derived for steady flow

For sheet flow conditions assume that ?gtgt?cr such
that the Einstein parameter becomes
and hence
Using this simplified formula the time-mean or
net bed load transport, Qb, can be expressed as
8
Class Exercise 6 By evaluating the integral
, show
that the net bed load transport rate is given by
This shows that the net bed load transport rate
is proportional to the asymmetry parameter W.
Recall that the result has neglected the
threshold of sediment motion.
9

• Suspended load beneath symmetrical and
  asymmetrical waves
• entrainment occurs above
• both rippled and plane beds

(i) Oscillating sheet flow measured with
conductivity concentration meter (CCM)
Large symmetrical waves U0 1.7 ms-1 T 7.2
s D50 0.21 mm
Delft Hydraulics Ribberink and Al Salem (1992)
10
Intra-wave concentrations measured (with OPCON
probe) at three heights in suspension
layer Cycle-mean concentration profiles
(power law profiles straight lines on log-log
plot)
11

• Cycle-mean concentration profile
• above plane beds
• ? simplified form of the Rouse profile

• vertical profile of cycle-mean concentration ltCgt
• has slope m ?1/2 on log-log plot
• ? m has the form of Rouse parameter

• Suspension above rippled beds
• entrainment is dominated by vortex formation and
  shedding
• in a near-bed layer of thickness equivalent
  to about 2 ripple heights
• effective convective mechanism for transporting
  sediment
• to significantly greater heights than above
  plane beds
• ? vortex shedding becomes important if the
  ripple steepness

12
Entrainment above vortex ripples in oscillatory
flow
13
Vortex shedding beneath symmetrical waves
? net transport above ripples depends upon degree
of asymmetry in the wave motion
Vortex shedding beneath asymmetrical waves
? vortex shedding gives rise to net transport in
direction opposite to that of wave advance (c.f.
flat bed case)
14
Cycle-mean concentration profile above rippled
beds ? despite convective nature of the vortex
shedding process, mean C-profile is usually
modelled using diffusive concepts
Upward diffusion Settling 0

• lt ..gt cycle-mean
• ?s sediment diffusivity
• ?s constant due to
• uniformity of vertical
• mixing in near-bed layer
• above ripples

in which decay scale Lr is related to ripple
height ?
15
Bed forms in oscillatory flow
Parameters involved in ripple formation at low
flow stages
Ripples in sinusoidal oscillatory flow are
generally ? long-crested ? symmetrical ?
regularly spaced with crests transverse to plane
of the orbital motion
Ripple development ? development of initially
flat bed as orbital diameter d0 increases ?
threshold of motion exceeded ?' 0.045
? first stage of ripple formation
initiated ? for small d0, ripple wavelength ? ?
d0 e.g
16

• ? ripple steepness gradually increases until
  vortex ripples develop with steepness 0.15
  ?/? 0.2
• ? flow separates in each wave cycle
• ripples attain a maximum steepness, (?/? )max
  0.2 - 0.22,
• and crest angles (up to 120?)

Field observations of ripple wavelength
17

• ? at very high flow stages (?SF 1), ripples are
  washed out and bed flattens
• ? substantial suspended load confined to thin
  oscillating sheet flow layer
• seabed is self regulating
• i.e. transport rates are capped
  beneath large (e.g. storm) waves
• Empirical formulae for ripple prediction e.g.
  Nielsen (1992).

• Field observations
• ? wave-generated ripples are widespread on the
  continental shelf
• (depths up to 50-100m)
• natural surface waves are irregular
• ? ripple properties are determined by wave
  spectrum
• ripple formation may be occasional (i.e. as a
  result of higher waves)
• ? fossil or relict ripples often remain in
  low wave conditions

18
Field observations (cont.)
Occurrence of ripples in the field Threshold of
motion is denoted by M Mc
M Mobility number
? maximum ripple wavelengths lt those in the
laboratory (for same sand size) ? ripples formed
by irregular waves are less steep than those
formed by regular waves ? bed roughness is less
than expected from laboratory
19

• Morphological modelling (for ripples)
• prediction of evolution of bed as a result of
  divergence in predicted sediment transport rate,
  e.g.
• Shear stress and transport distribution over
  surface of a ripple in steady flow

? maximum bed shear stress (skin friction)
occurs just upstream of crest ? critical
condition for ripple growth ? ripple profile will
grow or be eroded locally according to sediment
continuity equation
n porosity of bed
? if , then
i.e. the bed level rises, and vice versa ?
advection-diffusion of sediment in suspension
should also be included in a comprehensive scheme
20

• Wave-current interaction in the seabed boundary
  layer
• ? combined effects of waves and currents
  represents general situation on continental
  shelf
• ? waves modify the tidal dynamics (i.e. alter
  mean currents) only in shallow coastal waters
  (depth hlt30m), but potentially affect sediment
  transport rates over entire shelf
• continuum of conditions arises between earlier
  limiting cases of
• (i) Currents Alone and (ii) Waves Alone
• STEADY Small Waves Large Waves WAVES
• CURRENT ? on a ? on a ?
• ALONE Strong Current Weak Current ALONE

e.g. composite drag coefficients / friction
factors necessary for practical purposes CD
Combined fw CURRENTS ??? Friction/Drag
??? WAVES ALONE Coefficient ALONE
21
? in bottom seabed boundary layer, waves and
currents interact nonlinearly, e.g. turbulent
kinetic energy (T.K.E.)
e.g. cycle-mean bed shear stress i.e. waves
enhance the current-generated stresses
Cycle-mean velocity profile in W C flow
22

• Prediction of sediment
• transport rates by W C
• peak bed shear stress in the
• wave cycle is often of central
• importance
• ? earlier considerations for currents alone and
  waves alone remain applicable, with modifications
  for wave-current interaction
• ? roughly speaking, waves stir up the bottom
  sediment while current transports the sediment

23
Practical sand transport model TRANSPOR Van Rijn
(1993) This is a process-based (algebraic not
numerical) approach. Predicted transport rates
in perpendicularly combined W C flow TRANSPOR
has been parameterised to produce the simpler
Soulsby-Van Rijn formula (Soulsby, 1997)
24
Soulsby-Van Rijn formula (see Soulsby, 1997)
where
with
and
depth-averaged current root-mean-square
wave orbital velocity
drag coefficient due to current alone
threshold current velocity given by Van Rijn
(1984) for

for
25
SI units must be used in the above equations
? slope of bed in streamwise direction,
positive if flow runs uphill h water
depth d50 median grain diameter z0 bed
roughness length 0.006 m s relative density
of sediment g acceleration due to gravity ?
kinematic viscosity of water D non-dimensional
grain diameter The formula applies to total
(bed plus suspended load) transport in combined
WC on horizontal and sloping beds. Term Asb
gives the bed load, and term Ass the suspended
load transport. The method is intended for
conditions in which the bed is rippled, and z0
should be set to 6mm. It was derived by
applying the principles of Grass (1981) who
developed one of the first WC formulations, and
it was calibrated against the transport curves
plotted by van Rijn (see previous sheet) based on
the TRANSPOR program. TRANSPOR itself was
calibrated using various field data. The bed
slope term (1-1.6tan?) is a commonly used device,
but is a less correct procedure than modifying
the threshold velocity for slope effects.
26
What governs long-term sediment transport
patterns on the continental shelf? ? effect of
waves on transport rates on site varies from day
to day, and seasonally ? largest contributions
to long-term transport are due to fairly large,
frequently occurring waves combined with currents
lying between mean spring- and neap-maxima ?
extreme events (e.g. major storms occurring
during spring tides) do not dominate long-term
transport, as often supposed