PowerPoint-presentatie

1
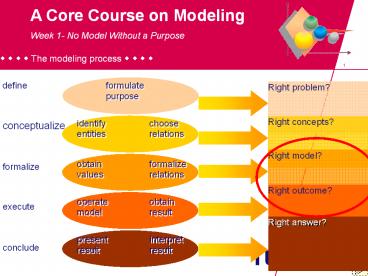
A Core Course on Modeling
Week 1- No Model Without a Purpose
? ? ? ? The modeling process ? ? ? ?
1
formulate purpose
identify entities
choose relations
obtain values
formalize relations
operate model
obtain result
present result
interpret result
2
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Contents ? ? ? ? ?

• What do we mean by Confidence?
• Validation and Verification, Accuracy and
  Precision
• Distributions to Indicate Uncertainty
• Distance and Similarity
• Confidence in Black Box models
• Features from Data Sets
• Example of the Value of a Black Box Model
• Validating a Black Box Model
• Confidence in Glass Box Models
• Structural Validity Assessment
• Quantitative Validity Assessment
• Summary
• References to lecture notes book
• References to quiz-questions and homework
  assignments (lecture notes)

3
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? What do we mean by Confidence? ? ? ? ?
?
3

• 96 of the contents
• of the universe
• is unknown dark
• matter energy
• so
• we cant have confidence
• in
• cosmological models

blueberry marmalade?
4
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? What do we mean by Confidence? ? ? ? ?
?
4

• Not quite
• confidence only assessible when
• modeled system
• model
• modeling purpose
• are all known

model
modeled system
represented by
needs
needs
confidence
should fulfill
with respect to
needs
purpose
5
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? What do we mean by Confidence? ? ? ? ?
?
5
example 1 elegant and simple model (elementary
secondary school physics, say mechanics of levers
and slides) modeled systems not explicitly
defined purpose to pass ones exam
6
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? What do we mean by Confidence? ? ? ? ?
?
6
example 1 elegant and simple model (elementary
secondary school physics, say mechanics of levers
and slides) modeled systems ship yard purpose
to secure safe launch
7
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? What do we mean by Confidence? ? ? ? ?
?
7
example 1 elegant and simple model (elementary
secondary school physics, say mechanics of levers
and slides) modeled systems ship yard purpose
to find direction of moving ship (uphill or
downhill?)
8
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? What do we mean by Confidence? ? ? ? ?
?
8
example 2 model full event log modeled systems
Internet traffic purpose diagnose performance
bottlenecks
9
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? What do we mean by Confidence? ? ? ? ?
?
9
example 2 model full event log modeled systems
Internet traffic purpose document for archiving
10
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? What do we mean by Confidence? ? ? ? ?
?
10
example 2 model aggregated data modeled
systems Internet traffic purpose document for
archiving
11
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? What do we mean by Confidence? ? ? ? ?
?
11
example 2 model aggregated data modeled
systems Internet traffic purpose analyse
performance bottlenecks
12
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? Validation and Verification, Accuracy and
Precision ? ? ?
12
Terms in the literature to discuss confidence

• Validation is it the right model?
• consistency model - modeled system
• e.g. are cat.-III values correct?
• does the model behave intuitively?
• consistency model - purpose
• e.g. are cat.-II values conclusive?

Valides strength
13
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? Validation and Verification, Accuracy and
Precision ? ? ?
13
Terms in the literature to discuss confidence

• Validation is it the right model?
• consistency model - modeled system
• e.g. are cat.-III values correct?
• does the model behave intuitively?
• consistency model - purpose
• e.g. are cat.-II values conclusive?

• verification is the model right?
• consistency conceptual - formal model
• e.g. are dimensions correct?
• is the graph a-cyclic?
• are values within admitted bounds cf.
  types?

Veritas truth
14
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? Validation and Verification, Accuracy and
Precision ? ? ?
14
Terms in the literature to discuss confidence
model
modeled system
conceptual
formal
represented by

• Validation is it the right model?
• consistency model - modeled system
• e.g. are cat.-III values correct?
• does the model behave intuitively?
• consistency model - purpose
• e.g. are cat.-II values conclusive?

needs
needs
confidence
should fulfill
with respect to
needs
purpose

• verification is the model right?
• consistency conceptual - formal model
• e.g. are dimensions correct?
• is the graph a-cyclic?
• are values within admitted bounds cf.
  types?

15
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? Validation and Verification, Accuracy and
Precision ? ? ?
15
Terms in the literature to discuss
confidence validation verification accuracy prec
ision
based on
16
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? Validation and Verification, Accuracy and
Precision ? ? ?
16
Terms in the literature to discuss
confidence validation verification accuracy prec
ision
?
?
high accuracy low precision
low accuracy high precision
low bias (offset, systematic error), large
spreading
low spreading (noise, randomness), large bias
a single result gives no information look at
ensembles
?
?
low accuracy low precision
high accuracy high precision
can only be assessed with ground truth
large spreading, large bias
low spreading, low bias
assessment needs no ground truth
(reproducibility)
outlier (freak accident, miracle, )
17
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Distributions to Indicate Uncertainty ?
? ? ? ?
17
Terms in the literature to discuss
confidence validation verification accuracy prec
ision
these all lead to uncertainty, represented as a
distribution giving the chance(density) of a
particular but uncertain outcome with some
average and some spreading.
distribution
18
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Distributions to Indicate Uncertainty ?
? ? ? ?
18
Terms in the literature to discuss
confidence validation verification accuracy prec
ision
these all lead to uncertainty, represented as a
distribution giving the chance(density) of a
particular but uncertain outcome with some
average and some spreading.
Gaussian (normal) distribution the sum of
sufficiently many uncorrelated numbers with
average ? and spreading ? has a normal
distribution. E.g. de weight distribution of
18-year old Americans.
19
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Distributions to Indicate Uncertainty ?
? ? ? ?
19
Terms in the literature to discuss
confidence validation verification accuracy prec
ision
these all lead to uncertainty, represented as a
distribution giving the chance(density) of a
particular but uncertain outcome with some
average and some spreading
Uniform distribution all outcomes in an interval
between ?-? and ?? have equal probability (e.g.,
dice ?3.5, ?2.5).
Distributions can be continuous (measuring) or
discrete (counting, e.g. dice)
20
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Distributions to Indicate Uncertainty ?
? ? ? ?
20
Uncertain model outcome and purpose Example 1.
model used for verification (e.g., diagnosis
classification good or bad.
high confidence
medium confidence
low confidence
Confidence for diagnosis support. Compare model
outcome against threshold. Confidence is lower if
areas left and right from treshold are less
different.
Validation is the treshhold at the right place?
Does checking with this treshhold mean anything
w.r.t. the purpose? Verification (for glass box)
do we calculate the distribution
correctly? Accuracy are we sure there is no
bias? Precision can we obtain narrower
distributions?
21
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Distributions to Indicate Uncertainty ?
? ? ? ?
21
Uncertain model outcome and purpose Example
2. model used in design computed uncertainty
intervals should be small enough to assess if A
or B is better.
high confidence
medium confidence
low confidence
A
B
A
A
A
A
Confidence for design decision support compare
one model outcome against a second model outcome.
Confidence is lower if the areas of two
distributions have larger overlap.
22
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Confidence in black box models ? ? ? ?
?
22
Black box models have empirical data as input.
Quantities try to capture essential behavior of
this data. Quantities typically involve
aggregarion. Most common aggregations average,
standard deviation, correlation, fit.
The black box in aircraft, although colored
orange for easier retrieval, is very much a black
box model in the sense that it only takes in
data. Confidence is black boxes is essential,
e.g. to reconstruct or diagnose the occurrences
during an incident.
univariate every item is a single quantity
bivariate every item is a pair of quantities
23
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Features from Data Sets ? ? ? ? ?
23
Average What is the central tendency in a
set? (mathematical details see datamodelling or
statistics courses)
Averages can be computed for all sorts of sets
provided that the properties of the elements
allow averaging. The average face is an
important concept in automated face recognition.
24
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Features from Data Sets ? ? ? ? ?
24
Standard deviation (? variance is ?2) How
closely packed is a set? (mathematical details
see datamodelling or statistics courses)
Standard deviation is a measure for the amount of
variation in a set of values.
25
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Features from Data Sets ? ? ? ? ?
25
Correlation (?) What is the agreement between
two sets (a measure for similarity)? (mathematica
l details see data modeling or statistics
courses)
Correlation is a form of similarity. An
interesting case is self-similarity sometimes an
object is similar to a scaled and perhaps
transformed copy of itself. Mathematical objects
called fractals are self-similar, but also some
natural objects (Romanesco broccoli ) classify as
(nearly) self similar.
26
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? Example of the Value of a Black Box Model
? ? ? ?
26
fit example of a extracting meaningful pattern
from data Example data set (xi,yi), assume
linear dependency yf(x). Intuition find a line
yaxb such that the sum of squares of the
vertical differences is minimal (mathematical
details see data modeling or statistics courses).
Patterns in data are often more valuable than the
unprocessed data. Hence the name data mining
for extracting this value.
very bad
still not good
try again
good (best?)
27
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Validating a Black Box Model ? ? ? ? ?
27
A black box model should explain the essence of a
body of data. Subtracting the explained part of
the data should leave little of the initial
data. For data (xi,yi), explained by a model
yf(x), the part left over is ?(yi-f(xi))2. This
should be small compared to ?(yi-?y)2 (what you
would get assuming no functional
dependency). Therefore confidence is high
iff ?(yi-f(xi))2/ ?(yi-?y)2 is ltlt1.
Residue literally means left over. To assess
confidence of a black box model, one should check
if there is not too much unexplained information
left in the initial data.
28
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Validating a Black Box Model ? ? ? ? ?
28
A black box model should be distinctive, that is
it should allow to distinguish input sets that
intuitively are distinct. Average, variance and
least squares may not be as distinctive as you
would like. Anscombe (1973) constructed 4 very
distinct data sets with equal average, variance
and least square fits. Early conclusion these
sets are similar.
29
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Validating a Black Box Model ? ? ? ? ?
29

• Raw data is reasonably well explained by lin.
  least squares fit (low residue). So what?
• Challenge hypothesis that raw data stems from one
  set. Cluster analysis reveals two sets.
• Conclusion 1 women will overtake men in 2050 ?
• Conclusion 2 men will break 0 second record
  around 2120 ?

Get even lower residuals with 4 clusters, taking
Jamaica or not Jamaica into account. Should
Olympic Games have Jamaican athletes in a
seperate category or not? What are the criteria
for justifiable segregation? (categories in
paralympics!)
What are the assumptions on which this conclusion
is based? Seek an argument from probabilities,
calculating error distributions of the
coordinates of the intersection point
This is impossible for physical reasons. But not
all black box models involve physics.
30
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Confidence in Glass Box Models ? ? ? ?
?
30
Glass box models computes values for output
variables in dependence on input
variables. Claim for every purpose, defined in
terms of output variabels, fulfilling the purpose
amounts to the uncertainty distribution on the
output variables to be sufficiently narrow. We
have seen an example on this sheet.
The value, produced by a glass box (model), can
be assessed via its output variables these
should have sufficiently narrow uncertainty
intervals (given the purpose!).
31
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Structural Validity Assessment ? ? ? ?
?
31
Qualitative validation (structural confidence) 1
examine dependencies in the functional network
The value, produced by a glass box (model), can
be assessed via its output variables these
should have sufficiently narrow uncertainty
intervals.
32
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Structural Validity Assessment ? ? ? ?
?
32
Qualitative validation (structural confidence) 1
examine dependencies in the functional network
expected
output
calculated
input
input
output
The value, produced by a glass box (model), can
be assessed via its output variables these
should have sufficiently narrow uncertainty
intervals.
select any pair of variables, and graphically
compare their dependency with what you expect,
tests the dependencies in between
33
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Structural Validity Assessment ? ? ? ?
?
33
Qualitative validation (structural confidence) 1
examine dependencies in the functional network
expected
output
calculated
input
output
The value, produced by a glass box (model), can
be assessed via its output variables these
should have sufficiently narrow ncertainty
intervals.
input
even if they involve multiple parallel
dependency routes
34
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Structural Validity Assessment ? ? ? ?
?
34
Qualitative validation (structural confidence) 1
examine dependencies in the functional network
output
expected?
calculated?
input
The value, produced by a glass box (model), can
be assessed via its output variables these
should have sufficiently narrow ncertainty
intervals.
output
and if there is no dependency, there is no
graph.
input
35
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Structural Validity Assessment ? ? ? ?
?
35
Qualitative validation (structural confidence) 1
examine dependencies in the functional network 2
examine of long range behavior is right
Asymptotic behavior is often simpler to predict
a glass box model at least should behave right in
the extremes
36
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Structural Validity Assessment ? ? ? ?
?
36
Qualitative validation (structural confidence) 1
examine dependencies in the functional network 2
examine of long range behavior is right 3
examine if singular behavior in isolated points
is right
Singular behavior of a model means the behavior
in exceptional conditions (e.g., something is 0,
two values are equal )
37
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Structural Validity Assessment ? ? ? ?
?
37
Qualitative validation (structural confidence) 1
examine dependencies in the functional network 2
examine of long range behavior is right 3
examine if singular behavior in isolated points
is right 4 examine if things that should
converge, have converged
validation
validation
validation
verification
Many mathematical results cannot be calculated in
closed form, but require contribution of ? many
terms. This can only be approximated, but we must
certify that at we include at least enough
terms.
38
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Quantitative Validity Assessment ? ? ?
? ?
38
Qualitative validation (structural confidence)
Quantitative validation
39
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Quantitative Validity Assessment ? ? ?
? ?
39
Quantitative validation a glass box as input ?
output function may amplify or dampen
uncertainties in its input.
output uncertainty
output uncertainty
Sensitivity a function can be said to react to
changes in its input. In case a function is very
sensitive, uncertainties in the input will
amplify to larger uncertainties in the output
Sensitivity the opposite is, when the function
hardly reacts on any changes in the input
input uncertainty
input uncertainty
40
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Quantitative Validity Assessment ? ? ?
? ?
40
For yf(x), spreading in x causes spreading in
y. For small ?x , we have ?y (?y / ?x) ?x ?
(dy/dx) ?x f (x) ?x So for relative
spreading ?y/y and ?x/x (expressed in ), we
have (?y/y) / (?x/x) f (x) x/y c(x)
(condition number). c(x)1 5 spread in x causes
5 spread in y. Large c(x) instable! Condition
number is the ratio in relative spreading between
output and input the propagation of
uncertainty.
Quantitative validation a glass box as input ?
output function may amplify or dampen
uncertainties in its input.
output uncertainty
output uncertainty
input uncertainty
input uncertainty
41
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Quantitative Validity Assessment ? ? ?
? ?
41
Quantitative validation a glass box as input ?
output function may amplify or dampen
uncertainties in its input. For yf(x), we
have (?y/y)c(x) (?x/x) What about
yf(x1,x2,x3,)? First try (?y/y)?i c(xi)
(?xi/xi). This is too pessimistic if xi are
independent, they will not all be extreme at
once. A better formula is (?y/y)2 ?i c2(xi)
(?xi/xi)2.
Most glass box models are functions with several
arguments. The uncertainties mix, by adding their
spreadings squared.
42
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Quantitative Validity Assessment ? ? ?
? ?
42

• Quantitative validation
• a glass box as input ? output function may
  amplify or dampen uncertainties in its input.
• (?y/y)2 ?i c2(xi) (?xi/xi)2 .
• Properties
• All ?xi occur squared. Therefore, spreading
  propertional to ?n rather than n for n arguments.
• All ci occur squared. So even if ?f/?xilt0 no
  compensation with negative contributions.
• One rotten apple
• To seek room for improvement, search for xi with
  large ?i and large ci.

Room for improvement sensitivity analysis helps
to assess if adding a functional expression will
improve the glass box model.
43
A Core Course on Modeling
Week 6-Models and Confidence
? ? ? ? ? Summary ? ? ? ? ?
43

• Modeling involves uncertainty because of
  different causes
• Differences between accuracy and precision
• Uncertainty ? distributions of values rather than
  a single value (normal, uniform)
• The notions of distance and similarity
• Confidence for black box models
• Common features of aggregation average, standard
  deviation and correlation
• Validation of a black box model
• Residual error how much of the behavior of the
  data is captured in the model?
• Distinctiveness how well can the model
  distinguish between different modeled systems?
• Common sense how plausible are conclusions,
  drawn from a black box model?
• Confidence for glass box models
• Structural validity do we believe the behavior
  of the mechanism inside the glass box?
• Quantitative validity what is the numerical
  uncertainty of the model outcome?
• Sensitivity analysis and the propagation of
  uncertainty in input data
• Sensitivity analysis to decide if a model should
  be improved.