Exploring Parameter Space PowerPoint PPT Presentation
Title: Exploring Parameter Space
1
X-ray Line Profile Diagnostics of Hot Star
Winds Roban H. Kramer1, David H. Cohen1, Stanley
P. Owocki2 (1) Swarthmore College, (2) Bartol
Research Institute, University of Delaware
Line Transport in an Expanding and
Continuum-Absorbing Medium Spherically Symmetric
Models with Absorption
Exploring Parameter Space Fits are performed by
calculating models for hundreds of combinations
of parameter values and finding the combination
that minimizes a fit statistic. This can be
visualized as mapping the value of the fit
statistic in a multi-dimensional volume in
parameter space.
The Line Profile Model is General It can
parameterize many different types of wind X-ray
distributions, allowing for the testing of
different physical theories.
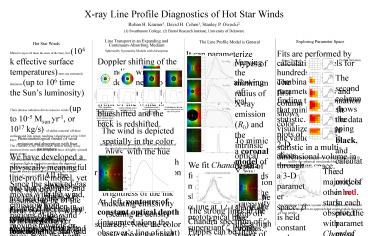
Hot Star Winds
Massive (up to 60 times the mass of the Sun), hot
(104 k effective surface temperatures) stars are
extremely luminous (up to 106 time the Suns
luminosity). Their intense radiation drives
massive winds (up to 10-5 Msun yr-1, or 1017
kg/s) of stellar material off their surfaces and
into space, reaching velocities of a few 1000
km/s. The Chandra X-ray Observatory detects
strong X-ray emission from such stars in spectral
lines of highly ionized heavy atoms. The
mechanism responsible for heating gas to the
millions of degrees Kelvin needed to produce the
observed ionization states is a mystery, but a
leading theory suggests shocks distributed
throughout the wind. Since the shocked gas moves
with the wind, emission from regions of the wind
moving towards or away from the Earth will be
Doppler shifted by a few 1000 km/s. Adding up
emission from the whole wind produces broad
profiles resolvable by Chandras
spectrograph. The cold, unshocked component of
the wind absorbs X-rays passing through it, so
the wind material along the line of sight to a
region affects how much of the emission from that
region will be detected by Chandra. Thus we can
use the shapes of lines in Chandra spectra to
infer the spatial and velocity structure of the
wind.
?1, q1/2
Doppler shifting of the expanding wind broadens
lines. To the observer on the left, the front of
the wind is blueshifted and the back is
redshifted.
Varying the minimum radius of X-ray emission (R0)
and the intrinsic optical depth of the wind (??)
affects the shape of the profiles. Larger minimum
radii exclude inner, slow-moving regions of the
wind, resulting in broader, flatter profiles.
Higher intrinsic optical depths obscure reddened
regions, skewing the line blueward. Far left are
contours of optical depth unity for different
values of ?? overlaying color velocity maps. Next
to them are the corresponding line profiles.
Profile Variation The second column shows the
data in black, and calculated models in red. In
each plot, the parameters of the red profile are
the best-fit values of q and u0, in a plane of
constant ??. The title of each plot gives the
values of ? , q, u0,??. The fit is only
performed on part of the line to avoid
contamination by a neighboring line at a longer
wavelength. For instance, in the first graph ??
is held at ?? 0 (remember, in all the graphs
?1). As the opacity of the wind (controlled by
??) is increased, notice how the predicted counts
in the redder parts of the line decrease.
Slices Through Parameter Space The first column
shows color plots of 2-D slices through a 3-D
parameter space. ? is held constant and models
are calculated for different values of q, u0 R
/R0, and ??. The red region is the 68.3
confidence region, orange is 95.4, yellow is
99.73 (each successively higher confidence level
includes all the points in the lower confidence
levels). Confidence intervals for a parameter
are found by projecting the 3-D confidence
regions onto 1 dimension. The 95.4 confidence
intervals for this fit are 0 lt q lt 0.4 0.5 lt u0 lt
1.0 ? R0 lt 2R 0.5 lt ?? lt 3.0
R0 1.5R?
R0 3R?
Thin, expanding, spherical shells produce
flat-topped line profiles broadened by the shell
velocity. Inner shells are slower and more dense,
giving narrower, taller profiles.
A continuous wind is built by integrating over
shells from some minimum radius.
Occultation by the star removes light from the
red edge of the profile.
A series of shells, added together, produce a
stepped profile.
R0 10R?
The wind is depicted spatially in the color
plots, with the hue indicating velocity with
respect to an observer on the left, and the
brightness of the ink indicating emissivity
(scaling as density squared). Note the color
scale above the third panel. Under each image is
the resulting line profile with the bluest
wavelengths (expressed in velocity units) on the
left, and the reddest on the right.
To mimic a coronal model of X-ray production we
let the emissivity drop off like a high power of
1/r, producing narrow profiles (left).
Phenomenological model of wind emission and
absorption with four parameters.
Including continuum absorption by the cold
component of the wind also preferentially removes
red photons.
We have developed a physically meaningful
line-profile model, yet one that is simple and
not tied to any one proposed mechanism of
hot-star X-ray production. Described in Owocki
Cohen (2001, ApJ, 559, 1108), the model assumes a
smoothly and spherically symmetrically
distributed accelerating X-ray emitting plasma
subject to continuum attenuation by the cold
stellar wind.
Many of the other hot stars observed with Chandra
are not fit well by the spherical wind model that
fits z Pup
We fit Chandra data from hot stars with this
model. Below we show the Ne X Lyman-a line at
12.13 Å in the prototypical blue supergiant z
Puppis. This star is a million times as luminous
as the sun and has a surface temperature of 42000
K (seven times solar).
The majority of other hot stars observed with
Chandra show line profiles that are broad but
symmetric. They cannot be fit by any spherically
symmetric wind model that includes significant
absorption. On the left is the 12.13 Å Ne X line
of ?1 Orionis c shown with the z Puppis best-fit
model. Notice how much narrower and more
symmetric the line is in this star.
All the emission physics is hidden in the
emissivity, h. Note that spherical coordinates
(m,r) are natural for the symmetry of the wind
emission.
The velocity is assumed to be of the form
v(r)v8(1-R?/r)b. With the observer looking at
the star and wind from one side, cylindrical
coordinates (p,z) are more natural.
where
At left, contours of constant optical depth
(integrated along the observers line of sight)
are overlay a velocity color map. The resulting
line profile (right) shows the effect of an
optically thick wind.
?? and b parameterize the absorption. And q and
Ro parameterize the radial X-ray filling factor,
thus the emissivity.
See Stephanie Tonnesens poster on the
Magnetically Confined Wind Shock Model for an
approach that might explain this type of line
profile.
The strong lines in the Chandra spectrum of z
Puppis can be fit by reasonable combinations of
wind parameters. These fits indicate that the
X-ray emitting plasma surrounding this star is
embedded in the accelerating and absorbing wind.
It is this delta function that allows us to map
m,r into wavelength, l. We solve these equations
numerically with Mathematica