Jonas De Vylder, Wilfried Philips - PowerPoint PPT Presentation
Jonas De Vylder, Wilfried Philips
IMPROVED FOURIER DESCRIPTORS FOR 2-D SHAPE REPRESENTATION Jonas De Vylder, Wilfried Philips Ghent University, Dept. Of Telecommunications and Information Processing – PowerPoint PPT presentation
Title: Jonas De Vylder, Wilfried Philips
1
IMPROVED FOURIER DESCRIPTORS FOR2-D SHAPE
REPRESENTATION
- Jonas De Vylder, Wilfried Philips
Ghent University, Dept. Of Telecommunications and
Information Processing
Jonas.DeVylder_at_telin.UGent.be
http//telin.ugent.be/ipi
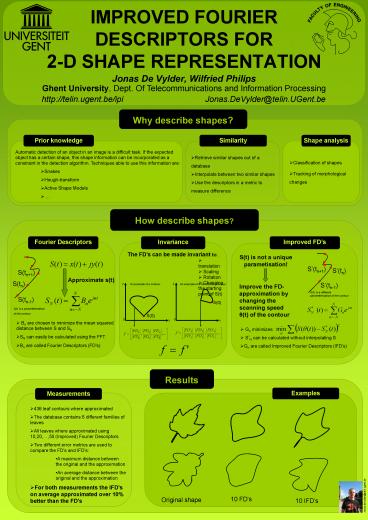
- Automatic detection of an object in an image is a
difficult task. If the expected object has a
certain shape, this shape information can be
incorporated as a constraint in the detection
algorithm. Techniques able to use this
information are - Snakes
- Hough-transform
- Active Shape Models
- Retrieve similar shapes out of a database
- Interpolate between two similar shapes
- Use the descriptors in a metric to measure
difference
- The FDs can be made invariant to
- translation
- Scaling
- Rotation
- Changing the starting point of S(t)
S(t) is not a uniqueparametisation!
S(tn1)
Approximate s(t)
S(tn)
y
An example of a contour
Improve the FD-approximation by changing the
scanning speed ?(t) of the contour
S(tn-1)
S(t) is a parameterisation of the contour
S(0)
0
x
- Bn are chosen to minimize the mean squared
distance between S and SN - SN can easily be calculated using the FFT
- Bn are called Fourier Descriptors (FDs)
- Gn minimizes
- SN can be calculated without interpolating S
- Gn are called Improved Fourier Descriptors
(IFDs)
- 436 leaf contours where approximated
- The database contains 6 different families of
leaves - All leaves where approximated using 10,20,,50
(Improved) Fourier Descriptors - Two different error metrics are used to compare
the FDs and IFDs - A maximum distance between the original and the
approximation - An average distance between the original and the
approximation - For both measurements the IFDs on average
approximated over 10 better than the FDs
Jonas.devylder_at_telin.ugent.be
10 FDs
Original shape
10 IFDs
PowerShow.com is a leading presentation sharing website. It has millions of presentations already uploaded and available with 1,000s more being uploaded by its users every day. Whatever your area of interest, here you’ll be able to find and view presentations you’ll love and possibly download. And, best of all, it is completely free and easy to use.
You might even have a presentation you’d like to share with others. If so, just upload it to PowerShow.com. We’ll convert it to an HTML5 slideshow that includes all the media types you’ve already added: audio, video, music, pictures, animations and transition effects. Then you can share it with your target audience as well as PowerShow.com’s millions of monthly visitors. And, again, it’s all free.
About the Developers
PowerShow.com is brought to you by CrystalGraphics, the award-winning developer and market-leading publisher of rich-media enhancement products for presentations. Our product offerings include millions of PowerPoint templates, diagrams, animated 3D characters and more.