Binary Search Trees

1
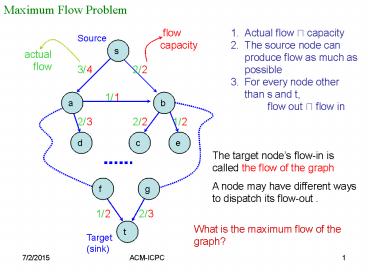
Maximum Flow Problem
flow capacity

1. Actual flow ? capacity
2. The source node can produce flow as much as
   possible
3. For every node other than s and t,
   flow out ? flow in

Source
s
actual flow
4
2
2/
3/
1
1/
b
a
3
2
2
1/
2/
2/
e
c
d
e
The target nodes flow-in is called the flow of
the graph
f
g
A node may have different ways to dispatch its
flow-out .
3
2
1/
2/
t
What is the maximum flow of the graph?
Target (sink)
2
What makes the maximum flow problem more
difficult than the shortest path problem?
Source
s
The shortest path of t is based on the shortest
path of g.
4
2
2/
3/
once a nodes shortest path from s is determined,
we will never have to revise the decision
1
1/
b
a
3
2
2
1/
2/
2/
e
c
d
e
The maximum flow to t is not based on the
maximum flows to f and g.
f
g
3
2
1/
2/
t
Target
3
local optimum does not imply global optimum
Source
Source
Source
s
s
s
5/5
2/2
4/5
2/2
5/5
2/2
1/1
0/1
a
1/1
a
b
a
b
b
3/3
4/4
2/3
1/4
0/3
3/3
3/4
3/3
1/3
d
0/3
d
3/3
c
d
1/3
c
c
Target
Target
2/2
5/5
s?c max flow 6
s?d max flow 7
t
Target
s?t max flow 7
4
A naïve approach adding all possible paths
together
Source
Source
Source
s
s
s
1
2
2/
1
1/
3
2
2/
1
1
1
a
a
a
b
b
b
4
1/
4
4
1
2
2/
1
3
2
2/
d
d
d
c
c
c
3
2/
1
1/
2
3
2/
t
t
t
Target
Target
Target
Residual Graph
Residual Graph
5
Source
Source
s
s
3/3
2/2
1
a
1
b
a
b
3
1/4
1
3
2/2
d
c
d
c
2
3/3
2/
t
t
Not always work.
Target
Target
We are just lucky
Residual Graph
6
We may have a wrong choice
Source
Source
s
s
3
3/
2
2
1
1
a
b
a
b
4
3/
1
3
2
3
2
d
c
d
c
2
3
3/
2
t
t
So, we keep a path for changing decision
Target
Target
7
Keep a path for changing decision
Source
Source
s
s
3
3/
2
2
3
1
1
a
b
a
b
4
3/
1
3
2
3
2
3
d
c
d
c
2
3
3/
2
3
t
t
Target
Target
Augmented Graph
8
Find another path in the augmented graph
No more path from s to t
Source
s
s
s
2
2/
3
2
2
3
3
1
a
1
1
b
a
a
b
b
2
1
3
2
2/
2/
3
1
2
1
2
1
3
2/
2
2
d
1
1
c
d
d
c
c
2
2/
3
2
2
3
3
t
t
t
Target
Augmented Graph
new Augmented Graph
9
Add flows together

Source

s
s
3
s
3
2
2
a
a
b
b
a
b
3
2
2
2
2
2
1
d
d
c
c
d
c
3
3
2
2
t
t
Target
t
Target
Target
Maximum Flow
10
An algorithm for finding the maximum flow of
graphs
Input G (V, E), and s,t ? V
Let Gmax (?, ?), Gaug G

1. Find a path p from s to t in Gaug
2. If no such p exists, output Gmax and stop the
   program
3. Add p into Gmax and update Gaug
4. Repeat 1, 2, and, if possible, 3

Complexity
O(f ?E)
11
Claim This algorithm always terminates with a
maximum flow of the input graph
The proof is somewhat difficult and beyond the
scope of 279.
Input G (V, E), and s,t ? V
Let Gmax (?, ?), Gaug G
I say No, it is not difficult and every one here
should know.

1. Find a path p from s to t in Gaug
2. If no such p exists, output Gmax and stop the
   program
3. Add p into Gmax and update Gaug
4. Repeat 1, 2, and 3 if possible

• Since any given graph has a finite maximum flow,
  and every path from s to t, if any, provides a
  positive flow, the program therefore cannot run
  forever.
• By contradiction, suppose the algorithm
  terminates with a flow in Gmax. that is not
  maximum.
• Then, there must be a flow not included in Gmax.
  But, if this is the case, there must be a path
  from s to t to carries this flow, and hence the
  program should not terminate at this moment. A
  contradiction.

12
An inefficient situation
Source
s
1000
1/
1/
1000
1/
1
1/
a
b
1
1/
1000
1000
1/
1/
t
Target
13
An inefficient situation
Source
s
1000
1/
2/
1000
1/
2/
1
1/
a
b
1000
1000
1/
1/
2/
2/
t
Target
14
Solution
Always chose the maximum next edge
Source
s
1000
1000/
1000
b
a
1000
1000
1/
1000/
t
Target