2.1 Functions and Their Graphs

1
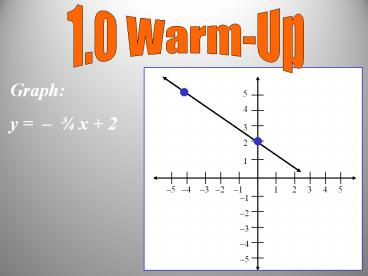
1.0 Warm-Up
Graph y ¾ x 2
2
1.0 Lines
Objective To be able to graph and write
equations of lines
3
GIVEN AN EQUATION OF A LINE
Slope - Intercept Form given slope and y -
intercept y mx b
Point - Slope Form given slope and a point
(x1,y1) y y1 m(x-x1)
4
Example 1 Write an equation of the line that
passes through (-3,4) and m 2/3
Use Point Slope y y1 m (x x1)
x1 -3 y1 4 m 2/3
y 4 2/3(x -3)
y 4 2/3 x 2
4
4
y 2/3 x 6
5

• Example 2
• Write an equation of the line that passes through
  (2,-3) and is
• Perpendicular to and
• Parallel to the line y 2x - 3

• Slope of a Perpendicular Line is m - ½
• Use Point Slope
• y y1 m(x x1)

x1 2 y1 -3 m 2/1
y -3 - 1/2 (x 2)
y 3 - 1/2 x 1
-3
-3
y - 1/2 x 2
6

• Example 2
• Write an equation of the line that passes through
  (2,-3) and is
• Perpendicular to and
• Parallel to the line y 2x - 3

b) Slope of a Parallel Line is m 2/1 Use
Point Slope y y1 m(x x1)
x1 2 y1 -3 m 2/1
y -3 2/1 (x 2)
y 3 2x 4
-3
-3
y 2x 7
7
Example 3 Write an equation of the line that
passes through (1,5) (4,2)
y y1 m (x x1)
y 5 - 1/1 (x 1)
y 5 - x 1
5
5
y - x 6
8
1.0 Homework
LINES WS
9
1.1 Warm-Up
Write an equation of the line that passes through
(-4, 1) and m -2
Use Point Slope y y1 m (x x1)
x1 -4 y1 1 m -2
y 1 -2(x -4)
y 1 -2 x - 8
1
1
y -2 x - 7
10
1.1 Functions and Graphs
Objective Students will be able to identify the
domain and range of a graph, identify when a
graph is a function, and be able to graph or
write the equation of a piecewise function
11
Part I Domain and Range
Domain Is the set of all input points (usually
your x value).
Range Is the set of all output points (usually
your y value).
12
Example 1 Graph the Relations (-3,-1), (-1, 1),
(1,1), (2,3) Then find the Domain and Range
Domain -3,-1,1,2
(2,3)
Range-1,1,3
(-1,1)
(1,1)
(-3,-1)
13
Example 2 Graph y 2x 3 Then find the
Domain and Range
Domain
All Real Numbers
Range
All Real Numbers
14
Example 3 Graph y x2 Then find the Domain
and Range
-2 -1 0 1 2
4
1
0
Domain
All Real Numbers
1
Range
y ? 0
4
15
Example 4 Here is the graph of y x Find
the Domain and Range
(1,1)
(0,0)
x ? 0
Domain
Range
y ? 0
16
Checking for Understanding
Use a graphing calculator to graph the functions.
Then find the domain and range.
17
Part II Functions
Function Is a relation when there is ONLY one
output for each input.
18
Example 5 Determine if the graph is a
function.
This is NOT A Function.
19
Example 6 Determine if the graph is a
function.
y -x2 4x 1
This is A Function.
20
Example 7 Graph y
Determine if the graph is a function.
4x2 x2 9
This is A Function.
21
Example 8 Determine if the graph is a function.

• x2 y2 25

This is NOT A Function.
22
Checking for Understanding
23
Part III Piecewise Functions
Piecewise Functions a function that is
represented by a combination of equations, each
corresponding to a part of the domain.
24
Try to write an equation for the graph below.
y or f(x)
2, if x ? -2
25
Example 9 Graph this function
26
(No Transcript)
27
Checking for Understanding
28
Checking for Understanding
29
1.1 HOMEWORK
30
1.2 Warm-Up
State the Domain and Range.
31
1.2 Mathmatical Models and Transformations
Objective Students will be able to investigate
different types of equations and their
transformations.
32
Power Function -
f(x) xa where a is a constant
Root Function -
Polynomial (state its degree) -
p(x) 2x6 x4 ½x3 1
Degree 6
Rational Function -
Is a ratio of two functions
Algebraic Function
Consists of algebraic operations (add,
subtract, mult., or divide)
Trigonometric Function -
f(x) sin x
Exponential Function -
f(x) ax
Logarithmic Function -
f(x) loga x
33
Transformations Activity
34
1.2 Homework
Pg. 35 36 1 5
35
1.3 Warm-Up

• Perform indicated operations

1.(2x7)2 2. 3 2
9
4x228x49
36
Operations on Functions
1.3 New Functions from Old Functions

• Operation Definition Example f(x)2x, g(x)x1

Addition f(x)g(x) 2x(x1) 3x1
Subtraction f(x) g(x) 2x (x1) x
1
Multiplication f(x)g(x) 2x(x1) 2x2 2x
37
Example 1
Adding and Subtracting Functions
f(x)3x, g(x)x2
h(x)f(x)g(x)
h(x)f(x) - g(x)
h(x)3x - (x2)
h(x)3x(x2)

• h(x)2x - 2

h(x)4x2
38
Example 2a
Multiplication and Division Functions
f(x)3x, g(x)x2
h(x)(f(x))(g(x))
h(x)f(x)/g(x)
h(x)(3x)(x2)

• h(x)3x26x

• h(x) 3x/(x2)

39
h(x) -5x 16
Example 2b
f(x) x 4, g(x) 3x
h(x) 2(f(x)) 2(g(x))
h(x) 4(f(x)) - 3(g(x))
h(x) (2x8) (6x)
h(x) (4x16) - (9x)
h(x) 8x 8
40
Composition of two functions

• The composition of the function f with the
  function g is
• f(g(x)) or (f ? g)(x) or
  f ? g

This is read as f of g of x
41
Example 3a

• f(x) 3x-1 and g(x) 2x 1

find f ? g
f(2x-1)
3(2x-1)-1

42
Example 3b

• f(x) x3 and g(x) x2 7

(g ? f)(2)
g(f(x))
g(x3)
g(23)
64 7
g(8)
71
82 7

43
1.3 Homework

• Pg. 47
• 31, 35, 37, 41 50,
• 54, And 55

44
1.4 Graphing Calculators
Objective Students will be able to investigate
graphs with different viewing windows or viewing
screens. Therefore learning how important it is
to choose the correct window.
45

• Example 1
• Draw the graph f(x) x2 3 in each of the
  following viewing rectangles.
• -2,2 by -2,2 b) -4,4 by -4,4
• c) -10,10 by -5,30 d) -50,50 by
  -100,100

46

• Example 2
• Draw the graph f(x) x3 150x. Which window is
  has the best display?
• -5,5 by -5,5
• b) -20,20 by -20,20
• c) -20,20 by -500,500
• d) -20,20 by -1000,1000

47
Example 3 Draw the graph f(x) With the
viewing window of a) -9,9 by -9,9 b)
-4.7,4.7 by -4.7,4.7
1 1 x
48
1.4 Homework
Pg. 53 54 1 5, 7, 11, and 13
49
1.5 Warm-Up
Exploring Exponential Functions Using a Graphing
Calculator

• Take out warm-up

50
1.5 Exponential Functions
Objective To be able to graph exponential
Functions.
Asymptote is the line that a graph approaches
as you move away from the origin.
51
Properties of Exponents
Let a and b be real numbers and let m and n be
integers.
Product of powers property
Power of power property
Power of product property
Negative exponent property
Zero exponent property
Quotient of powers property
Power of a quotient property
52
Exponential Functions involves the
expression y abx
base is the value b, with the exponent
y 4(3)x
y 3(½)x
53
Example 1 Graph the function a) y 2/3
(2)x
1) First draw an x/y box and find 2 points
2/3
4/3
54

• Example 2
• Graph the function
• y 4 ( 2/5 )x

1) First draw an x/y box and find 2 points
4
8/5
55
To graph y ab(x-h) k, begin by graphing
y abx. Then translate the graph horizontally
by h units and vertically k units.
Example 3 Graph y 23(x-2) 1
1) First graph y 23x
2) Then move h units horizontally and k units
vertically
0 1
2
6
h 2 k 1
56
THE NATURAL BASE e
The natural base e is irrational. It is defined
as follows As n approaches ?, (1 1/n)n
approaches e ? 2.718281828459
57
1.5 Homework
Pg. 62 3 16
58
1.6 Warm-Up
Evaluate the compositions if f(x) x 2 g(x)
3 h(x) x2 3
1. f(g(x)) 2. h(f(x)) 3. h(f(g(x)))
f(3)
h(x 2)
h(f(3))
f(x) x 2
h(x) x2 3
h(3 2)
3 2
(x 2)2 3
h(5)
52 3
5
x2 4x 4 3
x2 4x 7
25 3 28
59
1.6 Inverse Functions and Logarithms
Objective Students will be able to solve
problems involving inverse functions. To be
able to evaluate logarithmic functions.
Solving for the Inverse
STEP 1 Switch the y and the x values.
STEP 2 Solve for y.
60
Example 1 Find the inverse of 10y 2x 4
10x 2y 4
2y -10x 4
y -5x 2
Answer y -1 -5x 2
61
Example 2 Find the inverse of y -3x 6
x -3y 6
x -3y 6
6 6
x 6 -3y
y (-1/3)x 2
Answer y -1 (-1/3)x 2
62
Example 3 Find the inverse of the function
f(x) x5
y x 5
x y 5
5 x y
63
1.6 Homework

• Find the Inverse Equation
• Y 2x 3
• y x2 1
• y x3 1
• f(x)
• f(x)

1 x3
2x 1 x 3
64
Logarithmic Functions
http//www.youtube.com/watch?vQbd0uSPG5yQ http/
/www.youtube.com/watch?v4Y-62Ti5_6s
The Richter Scale
65
Logarithmic Functions
logby x if and only if bx y The expression
logby is read as log base b of y.
66

• Example 4
• Rewrite the logarithmic equation in exponential
  form.
• log3 9 2 b) log8 1 0 c) log5 (1/25) -2

32 9
80 1
5(-2) 1/25

• Example 5
• Evaluate the expression.
• log4 64 b) log3 27 c) log6 ( 1/36 )

4 x 64
3 x 27
6 x 1/36
x -2
x 3
x 3
67
Properties of Logarithms
Properties of Logarithms
Product Property logb uv logb u logb v
Quotient Property logb (u/v) logb u - logb v
Power Property logb un n logb u
68
Example 2 Expand log5 2x 6
log5 2 log5 x 6
log5 2 6 log5 x
69
Example 3 Condense 2 log3 7 5 log3 x
log3 7 2 log3 x 5
70
1.6 Homework
Pg. 76 35, 36, 39, and 40