Finite M/M/1 queue

1
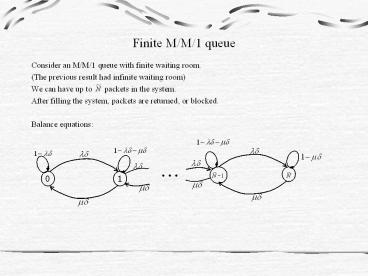
Finite M/M/1 queue

• Consider an M/M/1 queue with finite waiting room.
• (The previous result had infinite waiting room)
• We can have up to packets in the system.
• After filling the system, packets are returned,
  or blocked.
• Balance equations

0
1
2

• We have a steady state distribution for all ?.
  Of particular interest is

3

• Consider any queue with blocking probability PB
  and load ? packets/second.
• Net arrival rate (1- PB) ?. Then ?
  (1- PB) ? throughput.
• From a different point of view,

system
4

• For M/M/1 queue of finite length,

5
M/M/m Queue

• There are m servers and the customers line up in
  one queue. The customer at the head of the queue
  is routed to the available server.
• Balance equations

0
1
.

m1
m2
m-1
m

6
(No Transcript)
7
Erlang C Formula
8
M/M/? Queue
9
M/M/m/m/ Queue

• There are m servers. If a customer upon arrival
  finds all servers busy, it does not enter the
  system and is lost. The m in ///m is the
  limit of the number of customers in the system.
  This model is used frequently in the traditional
  telephony. To use in the data networks, we can
  assume that m is the number of virtual circuit
  connections allowed.
• Balance equations

.
m-1
m
0
1
10
(No Transcript)
11
(No Transcript)
12
Multi-Dimensional Markov Chain

• Consider transmission lines with m independent
  circuits of equal capacity. There are two types
  of sessions

13
Transition Probability Diagram
m, 0
m-1, 0
m-1, 1
. . .
. . .
. . .
1, m-1
1,0
1,2
1,1
. . .
0, m-1
0, m
0,2
0,1
0,0
14

• Suppose in the previous case, there is a limit k
  lt m on the number of circuits that can be used by
  sessions of type 1.

k,0
k,1
k, m-k
.
k-1, 2
k, m-k
k-1, 1
k-1,0
.
k-1, m-k-1
.
.
.
.
.
1, m-1
1,0
.
1,2
1,1
0, m
0, m-1
.
0,2
0,1
0,0
Blocking probabilities for call types
15

• Method of fining the steady state solutions for
  multi dimensional Markov Chain.

16
Truncation of Multi Dimensional System

• Consider l M/M/1 in independent queues.
• Then, for the joint queue, the following is true
• Above is also true for M/M/m, M/M/?, M/M/m/m, and
  all other birth-death processes.
• We now consider truncation of multi dimensional
  Markov Chain. Truncation is achieved by
  eliminating (or not considering) some of the
  states with low probability. The truncated system
  is a Markov Chain with the same transition
  diagram without some of the states that have been
  eliminated.

17
Claim Stationary distribution of the truncated
system is in a product form.

• Proof We have detailed balance equations
• Substituting we can show that balance
  
• equations hold true with
  
• Since the solution
  satisfies the
  balance equations,
• it must the unique stationary distribution.

18
Example Blocking Prob of Two Call Types
19
Important Results for M/G/1 Queue

• Pollaczek-Khinchin Formula