Layers of a DBMS

1
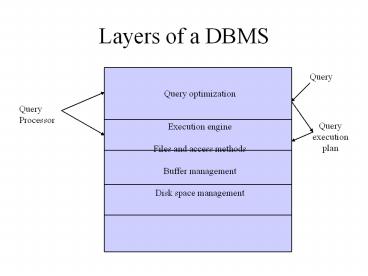
Layers of a DBMS
Query
Query optimization Execution engine Files and
access methods Buffer management Disk space
management
Query Processor
Query execution plan
2
The Memory Hierarchy
Main Memory Disk
Tape

• 5-10 MB/S
• transmission rates
• 2-10 GB storage
• average time to
• access a block
• 10-15 msecs.
• Need to consider
• seek, rotation,
• transfer times.
• Keep records close
• to each other.

• 1.5 MB/S transfer rate
• 280 GB typical
• capacity
• Only sequential access
• Not for operational
• data

• Volatile
• limited address
• spaces
• expensive
• average access
• time
• 10-100 nanoseconds

Cache access time 10 nanos
3
Disk Space Manager

• Task manage the location of pages on disk (page
  block)
• Provides commands for
• allocating and deallocating a page
• on disk
• reading and writing pages.
• Why not use the operating system
• for this task?
• Portability
• Limited size of address space
• May need to span several
• disk devices.

Spindle
Disk head
Sector
Platters
4
Buffer Management in a DBMS
Page Requests from Higher Levels
BUFFER POOL
disk page
free frame
MAIN MEMORY
DISK
choice of frame dictated by replacement policy

• Data must be in RAM for DBMS to operate on it!
• Table of ltframe, pageidgt pairs is maintained.

5
Buffer Manager
Manages buffer pool the pool provides space for
a limited
number of pages from disk. Needs to decide on
page replacement policy. Enables the higher
levels of the DBMS to assume that the needed data
is in main memory. Why not use the Operating
System for the task?? - DBMS may be able to
anticipate access patterns - Hence, may also be
able to perform prefetching - DBMS needs the
ability to force pages to disk.
6
Record Formats Fixed Length
F1
F2
F3
F4
L1
L2
L3
L4
Base address (B)
Address BL1L2

• Information about field types same for all
  records in a file stored in system catalogs.
• Finding ith field requires scan of record.
• Note the importance of schema information!

7
Files of Records

• Page or block is OK when doing I/O, but higher
  levels of DBMS operate on records, and files of
  records.
• FILE A collection of pages, each containing a
  collection of records. Must support
• insert/delete/modify record
• read a particular record (specified using record
  id)
• scan all records (possibly with some conditions
  on the records to be retrieved)

8
File Organizations

• Heap files Suitable when typical access is a
  file scan retrieving all records.
• Sorted Files Best if records must be retrieved
  in some order, or only a range of records is
  needed.
• Hashed Files Good for equality selections.
• File is a collection of buckets. Bucket primary
  page plus zero or more overflow pages.
• Hashing function h h(r) bucket in which
  record r belongs. h looks at only some of the
  fields of r, called the search fields.

9
Cost Model for Our Analysis

• As a good approximation, we ignore CPU costs
• B The number of data pages
• R Number of records per page
• D (Average) time to read or write disk page
• Measuring number of page I/Os ignores gains of
  pre-fetching blocks of pages thus, even I/O cost
  is only approximated.

10
Cost Model for Our Analysis

• As a good approximation, we ignore CPU costs
• B The number of data pages
• R Number of records per page
• D (Average) time to read or write disk page
• Measuring number of page I/Os ignores gains of
  pre-fetching blocks of pages thus, even I/O cost
  is only approximated.
• Average-case analysis based on several
  simplistic assumptions.

11
Assumptions in Our Analysis

• Single record insert and delete.
• Heap Files
• Equality selection on key exactly one match.
• Insert always at end of file.
• Sorted Files
• Files compacted after deletions.
• Selections on sort field(s).
• Hashed Files
• No overflow buckets, 80 page occupancy.

12
Cost of Operations

13
Cost of Operations
14
Indexes

• An index on a file speeds up selections on the
  search key fields for the index.
• Any subset of the fields of a relation can be the
  search key for an index on the relation.
• Search key is not the same as key (minimal set of
  fields that uniquely identify a record in a
  relation).
• An index contains a collection of data entries,
  and supports efficient retrieval of all data
  entries k with a given key value k.

15
Alternatives for Data Entry k in Index

• Three alternatives
• Data record with key value k
• ltk, rid of data record with search key value kgt
• ltk, list of rids of data records with search key
  kgt
• Choice of alternative for data entries is
  orthogonal to the indexing technique used to
  locate data entries with a given key value k.
• Examples of indexing techniques B trees,
  hash-based structures

16
Alternatives for Data Entries (2)

• Alternative 1
• If this is used, index structure is a file
  organization for data records (like Heap files or
  sorted files).
• At most one index on a given collection of data
  records can use Alternative 1. (Otherwise, data
  records duplicated, leading to redundant storage
  and potential inconsistency.)
• If data records very large, of pages
  containing data entries is high. Implies size of
  auxiliary information in the index is also large,
  typically.

17
Alternatives for Data Entries (3)

• Alternatives 2 and 3
• Data entries typically much smaller than data
  records. So, better than Alternative 1 with
  large data records, especially if search keys are
  small.
• If more than one index is required on a given
  file, at most one index can use Alternative 1
  rest must use Alternatives 2 or 3.
• Alternative 3 more compact than Alternative 2,
  but leads to variable sized data entries even if
  search keys are of fixed length.

18
Index Classification

• Primary vs. secondary If search key contains
  primary key, then called primary index.
• Clustered vs. unclustered If order of data
  records is the same as, or close to, order of
  data entries, then called clustered index.
• Alternative 1 implies clustered, but not
  vice-versa.
• A file can be clustered on at most one search
  key.
• Cost of retrieving data records through index
  varies greatly based on whether index is
  clustered or not!

19
Clustered vs. Unclustered Index
Data entries
Data entries
(Index File)
(Data file)
Data Records
Data Records
CLUSTERED
UNCLUSTERED

20
Index Classification (Contd.)

• Dense vs. Sparse If there is at least one data
  entry per search key value (in some data
  record), then dense.
• Alternative 1 always leads to dense index.
• Every sparse index is clustered!
• Sparse indexes are smaller

Ashby, 25, 3000
22
Basu, 33, 4003
25
Bristow, 30, 2007
30
Ashby
33
Cass, 50, 5004
Cass
Smith
Daniels, 22, 6003
40
Jones, 40, 6003
44
44
Smith, 44, 3000
50
Tracy, 44, 5004
Sparse Index
Dense Index
on
on
Data File
Name
Age
21
Index Classification (Contd.)

• Composite Search Keys Search on a combination of
  fields.
• Equality query Every field value is equal to a
  constant value. E.g. wrt ltsal,agegt index
• age20 and sal 75
• Range query Some field value is not a constant.
  E.g.
• age 20 or age20 and sal gt 10

Examples of composite key indexes using
lexicographic order.
11,80
11
12
12,10
name
age
sal
12,20
12
bob
10
12
13,75
13
cal
80
11
ltage, salgt
ltagegt
joe
12
20
sue
13
75
10,12
10
20
20,12
Data records sorted by name
75,13
75
80,11
80
ltsal, agegt
ltsalgt
Data entries in index sorted by ltsal,agegt
Data entries sorted by ltsalgt
22
Tree-Based Indexes

• Find all students with gpa gt 3.0
• If data is in sorted file, do binary search to
  find first such student, then scan to find
  others.
• Cost of binary search can be quite high.
• Simple idea Create an index file.

Index File
kN
k2
k1
Data File
Page N
Page 1
Page 3
Page 2

• Can do binary search on (smaller) index file!

23
Tree-Based Indexes (2)
index entry
P
K
P
K
P
P
K
m
0
1
2
1
m
2
Root
24
B Tree The Most Widely Used Index

• Insert/delete at log F N cost keep tree
  height-balanced. (F fanout, N leaf pages)
• Minimum 50 occupancy (except for root). Each
  node contains d lt m lt 2d entries. The
  parameter d is called the order of the tree.

Root
25
Example B Tree

• Search begins at root, and key comparisons direct
  it to a leaf.
• Search for 5, 15, all data entries gt 24 ...

30
17
24
13
39
3
5
19
20
22
24
27
38
2
7
14
16
29
33
34

26
B Trees in Practice

• Typical order 100. Typical fill-factor 67.
• average fanout 133
• Typical capacities
• Height 4 1334 312,900,700 records
• Height 3 1333 2,352,637 records
• Can often hold top levels in buffer pool
• Level 1 1 page 8 Kbytes
• Level 2 133 pages 1 Mbyte
• Level 3 17,689 pages 133 MBytes

27
Inserting a Data Entry into a B Tree

• Find correct leaf L.
• Put data entry onto L.
• If L has enough space, done!
• Else, must split L (into L and a new node L2)
• Redistribute entries evenly, copy up middle key.
• Insert index entry pointing to L2 into parent of
  L.
• This can happen recursively
• To split index node, redistribute entries evenly,
  but push up middle key. (Contrast with leaf
  splits.)

28
Inserting 8 into Example B Tree

• Note
• why minimum occupancy is guaranteed.
• Difference between copy-up and push-up.

Entry to be inserted in parent node.
(Note that 5 is
s copied up and
5
continues to appear in the leaf.)
3
5
2
7
8
appears once in the index. Contrast
29
Example B Tree After Inserting 8
Root
17
24
30
13
5
2
3
39
19
20
22
24
27
29
33
34
38
7
5
8
14
16

• Notice that root was split, leading to increase
  in height.

• In this example, we can avoid split by
  re-distributing entries however,
  this is usually not done in practice.

30
Deleting a Data Entry from a B Tree

• Start at root, find leaf L where entry belongs.
• Remove the entry.
• If L is at least half-full, done!
• If L has only d-1 entries,
• Try to re-distribute, borrowing from sibling
  (adjacent node with same parent as L).
• If re-distribution fails, merge L and sibling.
• If merge occurred, must delete entry (pointing to
  L or sibling) from parent of L.
• Merge could propagate to root, decreasing height.

31
Example Tree After (Inserting 8, Then) Deleting
19 and 20 ...
Root
17
27
30
13
5
2
3
39
33
34
38
7
5
8
22
24
27
29
14
16

• Deleting 19 is easy.
• Deleting 20 is done with re-distribution. Notice
  how middle key is copied up.

32
... And Then Deleting 24

• Must merge.
• Observe toss of index entry (on right), and
  pull down of index entry (below).

30
39
22
27
38
29
33
34
13
5
30
17
3
39
2
7
22
38
5
8
27
29
33
34
14
16
33
Multidimensional Indexes

• Applications geographical databases, data cubes.
• Types of queries
• partial match (give only a subset of the
  dimensions)
• range queries
• nearest neighbor
• Where am I? (DB or not DB?)
• Conventional indexes dont work well here.

34
Indexing Techniques

• Hash like structures
• Grid files
• Partitioned indexing functions
• Tree like structures
• Multiple key indexes
• kd-trees
• Quad trees
• R-trees

35
Grid Files

• Each region in the file
• corresponds to a
• bucket.
• Works well even if
• we only have partial
• matches
• Some buckets may
• be empty.
• Reorganization requires
• moving grid lines.
• Number of buckets
• grows exponentially
• with the dimensions.

500K







250K


200K

90K


Salary



10K

0
15
20
35
102
Age
36
Partitioned Hash Functions

• A hash function produces k bits identifying the
  bucket.
• The bits are partitioned among the different
  attributes.
• Example
• Age produces the first 3 bits of the bucket
  number.
• Salary produces the last 3 bits.
• Supports partial matches, but is useless for
  range queries.

37
Tree Based Indexing Techniques
Salary, 150
Age, 60
Age, 47
70, 110
Salary, 300
85, 140













38
Multiple Key Indexes

• Each level as an index for one
• of the attributes.
• Works well for partial matches
• if the match includes the first
• attributes.

Index on first attribute
Index on second attribute
39
KD Trees
Adaptation to secondary storage

• Allow multiway branches
• at the nodes, or
• Group interior nodes
• into blocks.

Salary, 150
Age, 60
Age, 47
50, 275
70, 110
Salary, 80
Salary, 300
60, 260
85, 140
50, 100
Age, 38
50, 120
30, 260
25, 400
45, 350
45, 60
25, 60
50, 75
40
Quad Trees

• Each interior node corresponds
• to a square region (or k-dimen)
• When there are too many points
• in the region to fit into a block,
• split it in 4.
• Access algorithms similar to those
• of KD-trees.

400K











Salary


0
100
Age
41
R-Trees

• Interior nodes contain sets
• of regions.
• Regions can overlap and not
• cover all parents region.
• Typical query
• Where am I?
• Can be used to store regions
• as well as data points.
• Inserting a new region may
• involve extending one of the
• existing regions (minimally).
• Splitting leaves is also tricky.