Comparing the two representations

1
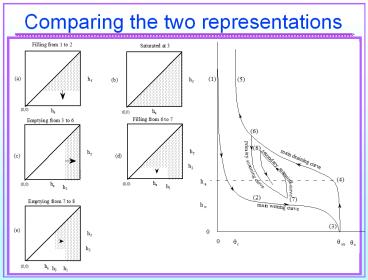
Comparing the two representations
2
1962 Poulovasilis Data-model
3
Did it graphically, now mathematically

• Stated mathematically as integrating over the
  domain of filled pores.
• Main wetting
• Main Draining
• Defining the
• turning point as
• Primary wetting

4
Notation for hysteretic process

• Need to keep track of turning points
• Subscripts denote the order of pressures, and
  relative position indicates whether the
  transition was wetting or drying. In the case
  shown, the media wetted from h0 to h1, dried to
  h2, and then re-wetted to the present pressure h.

5
dis-functional

• Curly brackets ? is not a function of h but
  is a functional of h. There is not a one-to-one
  mapping between ? and h without consideration of
  the antecedent conditions.
• Can relate ? and h from a known initial state and
  through a known sequence of either ? or h as
  stated in equation 2.66

6
How to obtain joint density function?

• Carry out a terrific number of experiments where
  you map out the entire domain of possible filling
  and draining pressures to obtain f(he,hf) by
  brute force.
• With computer control this is feasible using an
  automated pressure cell.

7
Similarity Theories

• 1973 Mualem introduced a simplification of this
  model noted that the joint density function
  f(he,hf) could be well approximated by the
  product of two univariate density functions
• f(he,hf) g(he)l(hf) 2.67
• g() and l() are probability density functions
  that depend only on he and hf, respectively.
• The filling pressure distributions are the same,
  up to a constant multiplier, along draining
  pressure lines
• Using this, only need the main filling and
  emptying curves to obtain g() and l().

8
Graphical Representation

• Similarity assumption of Mualem (1973)

9
Mualems similarity data-model
10
And to make life even easier...

• Parlange (1976) similarity model based on data
  from the main draining curve alone is sufficient
  to reproduce the full family of scanning curves.

11
Parlanges model-data