Mealy Machine

1
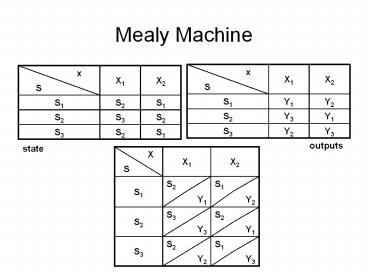
Mealy Machine
x X1 X2
S X1 X2
S1 S1 Y1 Y2
S2 S2 Y3 Y1
S3 S3 Y2 Y3
x X1 X2
S X1 X2
S1 S1 S2 S1
S2 S2 S3 S2
S3 S3 S2 S1
outputs
state
X X1 X1 X2 X2
S X1 X1 X2 X2
S1 S1 S2 S1
S1 S1 Y1 Y2
S2 S2 S3 S2
S2 S2 Y3 Y1
S3 S3 S2 S1
S3 S3 Y2 Y3
2
State table of Mealy Machine
x X1 X2
S X1 X2
S1 S1 S2 S1
S2 S2 S3 S2
S3 S3 S2 S1
S Y
S1 Y2
S2 Y1
S3 Y3
3
Mealy Machine Graph
X X1 X1 X2 X2
S X1 X1 X2 X2
S1 S1 S2 S1
S1 S1 Y1 Y2
S2 S2 S3 S2
S2 S2 Y3 Y1
S3 S3 S2 S1
S3 S3 Y2 Y3
4
Moore Machine Graph
x X1 X2 Y
S X1 X2 Y
S1 S1 S2 S1 Y2
S2 S2 S3 S2 Y1
S3 S3 S2 S1 Y3
5
Natural language formulation of a problem

• Design a control unit for ligth signalization on
  the railway with car sensors in positions A, B,
  C. The cars can go B?A, A?B i A?C.
• In direction B?A go only car sets of length
  larger than the distance between sensors B and A.
  
• In directions A?B and A?C go only single cars of
  length smaller than distance between sensors A
  and B and A and C, respectively.

The designed circuit should light lamp z1 if
there are no cars between sensors A and B or
sensors A and C Sensors A, B, C generate signals
a1, b1 and c1 respectively, when sets of cars
or single cars occur to be in their close
distance.
6
Timing Diagram Specification
7
Transition and output table for light
signalization circuit
ABC 000 001 011 010 110 111 101 100 Z
S 000 001 011 010 110 111 101 100 Z
S1 S1 S1 - - S6 - - - S2 0
S2 S2 S3 - - - - - - S2 1
S3 S3 S3 S5 - S4 - - - - 1
S4 S4 S1 - - S4 - - - - 1
S5 S5 S1 S5 - - - - - - 1
S6 S6 - - - S6 S7 - - - 1
S7 S7 - - - - S7 - - S8 1
S8 S8 S1 - - - - - - S8 1
8
Moore Machine graph for the analyzed device
000
9
asynchronous flip-flop sr
Q(t)?Q(t1) Q(t)?Q(t1) s r
0 0 0 -
0 1 1 0
1 0 0 1
1 1 - 0
s r Q(t1)
0 0 Q(t)
0 1 0
1 0 1
1 1 -
10
Asynchronous sr flip-flop
11
Asynchronous flip-flop sr
s r Q(t1)
0 0 Q(t)
0 1 0
1 0 1
1 1 -
12
Negated sr FF

• This version has negated inputs
• This FF realizes the function

Q(t1)
0 0 -
0 1 1
1 0 0
1 1 Q(t)
Q(t)?Q(t1) Q(t)?Q(t1)
0 0 - 0
0 1 0 1
1 0 1 0
1 1 0 -
13
Negated sr FF
14
Negated sr FF
Q(t1)
0 0 -
0 1 1
1 0 0
1 1 Q(t)