Development of Bondgraph Models for Power Electronic Systems

1
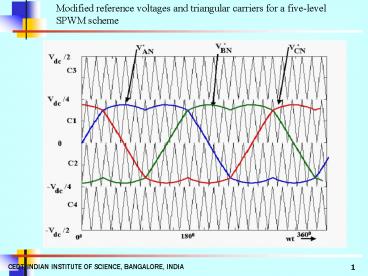
Modified reference voltages and triangular
carriers for a five-level SPWM scheme
2
The inverter switching vectors and their
switching time durations during sampling interval
TS (Reference voltages are within the inner
carrier region, M lt 0.433)
3
Determination of the Ta_cross , Tb_cross and
Tc_cross during switching interval TS (When
reference voltages are spanning the inner carrier
region, M lt 0.433)
4
Determination of the Ta_cross , Tb_cross and
Tc_cross during switching interval TS (When
reference voltages are spanning the inner carrier
region, M lt 0.433)
5
Determination of the Ta_cross , Tb_cross and
Tc_cross during switching interval TS (When
reference voltages are spanning the entire
carrier region, 0.433ltM lt 0.866)
6
Determination of the Ta_cross , Tb_cross and
Tc_cross during switching interval TS (When
reference voltages are spanning the entire
carrier region, 0.433ltM lt 0.866)
7
SUMMARY Ta_cross , Tb_cross and Tc_cross for
various carrier regions
8
Space Vector PWM signal generation for
multi-level inverters using only the sampled
amplitudes of reference phase voltages
Equivalence to Conventional SVPWM

• The reference signals in carrier based SVPWM are
  shifted to one carrier region
• The outer sub-hexagon in the conventional SVPWM
  are shifted to central sub-hexagon in
  conventional SVPWM
• The reference signal shifting in carrier based
  SVPWM is equivalent to sub-hexagonal shifting in
  the conventional SVPWM

9
Algorithm for inverter leg switching time
calculation
, x a, b, c
10
The traces of Tfirst_cross , Tsecond_cross and
Tthird_cross showing non-centered time duration
for middle vectors
11
The traces of Tg_first_cross , Tg_second_cross
and Tg third_cross showing centered time duration
for middle vectors
12
Toffset1 Toffset2 waveforms for various
modulation indices
13
Tas Toffset2 Toffset2 waveforms
14
Generalization for n level PWM (n even)
15
Generalization for n level PWM (n odd)
16
Generalization for n level PWM
n even
n odd
17
Proposed SVPWM signal generation in
over-modulation
18
Proposed SVPWM signal generation in
over-modulation
19
Proposed SVPWM signal generation in
over-modulation
20
Proposed SVPWM signal generation in
over-modulation
21
Proposed SVPWM signal generation in
over-modulation
22
Proposed SVPWM signal generation in
over-modulation
23
Summary linear range of modulation
24
Summary over-modulation condition
25
Inverter configuration
26
Phase-A voltage and phase-A current waveforms for
modulation index 0.15 (Layer 1 operation).
27
Plot of Tga and offset time Toffset1 Toffset2
for modulation index 0.15 (Layer 1 operation).
DAC output
28
Phase-A voltage and phase-A current waveforms for
modulation index 0.3 (Layer 2 operation).
29
Plot of Tga and offset time Toffset1 Toffset2
for modulation index 0.3 (Layer 2 operation)
DAC output
30
Phase-A voltage and phase-A current waveforms for
modulation index 0.6 (Layer 3 operation).
31
Plot of Tga and offset time Toffset1 Toffset2
for modulation index 0.6 (Layer 3 operation)DAC
output
32
The phase-A voltage and phase-A current waveforms
for modulation index 0.85 (Layer 4
operation).
33
Plot of Tga and offset time Toffset1 Toffset2
for modulation index 0.85 (Layer 4 operation)
DAC output
34
The phase-A voltage and phase-A current waveforms
for modulation index 1.15 (over-modulation).
35
Phase-A current waveform for speed reversal from
40Hz to -40 Hz modulation index 0.70
36
Space Phasor Based Self Adaptive Current
Hysteresis Controller
37
A Space Phasor Based Self Adaptive Current
Hysteresis Controller Using Adjacent Inverter
Voltage Vectors with Smooth Transition to Six
Step Operation for a Three Phase Voltage Source
Inverter
38
Introduction

• A self adaptive space phasor based current
  hysteresis
• controller is proposed for a voltage source
  inverter
• Current error space phasor is held within a
  hexagonal
• boundary
• Current errors are monitored along jA, jB , jC
  axes
• Ensures optimum switching
• Does not require computations, uses simple look
  up table
• Uses a self adaptive sector change logic

39
Current error space phasor
The combine effect of the three current errors
can be represented as a space phasor
The current error space phasor is kept within a
boundary by switching an appropriate voltage
vector The nearest vector is selected
40

This equation defines the direction in
which current error space phasor moves
41
Directions of current error space phasor in
sector -1
42
Vectors to be switched in sector-1 to bring back
the error
R1
V2
R2
VZ
R3
43
Directions of current error space phasor in
sector -2
44
Vectors to be switched in sector-2 to bring back
the error
V2
V3
VZ
45
Vectors to be switched in different sectors
46
The combined error boundary
47
Region identification
Modified regions for odd sectors
Modified regions for even sectors
48
Region identification contd.
49
Detecting The Sector Change
Current error space phasor moves out through a
unique axis during sector change
50
Sector Change Detected using an outer hysteresis
51
Over modulation
Sector 1
Switching between the active vectors , V1 and V2
52
Over modulation
Sector change logic for over modulation region
53
Simulation Results
The error boundary
Sectors Vectors Nearest vectors are selected
in every sector
54
Simulation Results . Over modulation
Error space phasor
Current space phasor
Transition to six step
55
Experimental Results
Phase voltage and current
The error boundary 1 div 0.3 Amp
56
Experimental Results
The machine current space phasor ( no load ) 1
div 1 amp
The machine current space phasor when loaded (
1 div 2 A mp )
57
Experimental Results
58
Experimental Results
Over modulation
Six step operation
Transition to six step mode
59
Experimental Results Over modulation
The machine current space phasor ( 1 div 3 A
mp )
The error boundary 1 div 1 amp
60
Salient Features
Space phasor based hysteresis controller with
optimum switching is proposed Self adaptive
sector change logic Smooth transition to over
modulation and to six step mode No computation
of machine back emf is required Uses simple look
up tables Ensures that only one inverter leg is
switched during transition of inverter state
61
Current Error Space Phasor Based Hysteresis PWM
Controller with Self Adaptive Logic and Adjacent
Voltage Vector Selection for The Entire
Modulation Range for Three-level Voltage Source
Inverter Fed Drive
62
Power Schematic of a Dual Two-level Voltage
Source Inverter Fed IM Drive
63
Combined Voltage Space Phasor Locations and
Inverter Switching Vector Combinations for
Three-level Inverter
24 Sectors 19 Vectors 64 Switching States
64
Directions of Current Error Space Phasor for Tip
of Vm in Sector -7
65
Directions of Current Error Space Phasor for Tip
of Vm in Sector -8
66
Directions of Current Error Space Phasor for Tip
of Vm in Sector 1 and Sector-2
67
Vectors to be Switched in Sector-7 to Keep the
Current Error Space Phasor Inside the Boundary
68
Vectors to be Switched in Sector-8 to Keep the
Current Error Space Phasor inside the Boundary
69
Vectors to be Switched in Different Sectors for
Different Regions
70
Vectors to be Selected in Different Sectors for
Different Regions
71
Clamping of Inverters for Adjacent Sectors
72
Comparators Used for Region Detection
73
Region Formation from the Segments of the
Hexagonal Boundary
When comparator along jA is ON and

else

74
Region Formation from the Segments of the
Hexagonal Boundary
75
Detecting The Sector Change Using an Outer
Hysteresis
76
Sector Change Detection for Two-level Operation
(Trajectory a)
Current error space phasor moves out through a
unique axis during a sector change
77
Mapping of Outer Sectors to Inner Sectors
78
Sets of Sector Changes Detected Along jA Axis and
jA Axis
79
Sector Change Along Corner to Corner Sectors
(Trajectory c)
Sector Change from 23 to 8 is Detected Along jA
Direction
80
Prevention of Jitter
Prevention of False Sector Change
81
Sector Change During Over Modulation (Trajectory
f)
82
Sector Change During Over Modulation (Sector-7 to
Sector-9)
Trajectory of Current Error Space Phasor
83
Sector Change During Over Modulation (Sector-9 to
Sector-10)
Trajectory of Current Error Space Phasor
84
Sector Detection Including Over Modulation
(Forward Rotation)
85
Simulation Results
Two-level operation
1 div. 0.6 A
86
Simulation Results
Transition from two-level to three-level
Transition from three-level to over modulation
87
Simulation Results
Three-level operation
1 div. 0.6 A
88
Simulation Results
Over modulation
1 div.0.6 A
Starting of the machine
89
Block Schematic of Experimental Set-up
90
Experimental Results
Two-level operation
1 div 0.3 Amp
1 div 0.75Amp
91
Experimental Results
Transition form two-level to three-level and vice
versa
92
Experimental Results
Three-level operation
1 div 0.3 Amp
1 div 0.75Amp
93
Experimental Results
Over modulation
1 div 0.75 Amp
94
Experimental Results
Starting of the machine
95
Experimental Results
Speed reversal of the machine
96
Experimental Results
Speed reversals of the machine
97
Experimental Results
Three-level operation
Two-level operation
Normalized harmonic spectrum of current waveforms
98
Experimental Results
Three-level operation
Two-level operation
Normalized harmonic spectrum of voltage waveforms
99
A HARMONIC ELIMINATION SCHEME FOR AN OPEN END
WINDING INDUCTION MOTOR DRIVE FED FROM TWO
INVERTERS WITH ASYMMETRICAL DC LINK VOLTAGES
100
Salient features

• A low order harmonic elimination technique for an
  openend winding induction motor drive is
  proposed.
• For the present openend winding drive, the
  induction motor is fed from two 2-level inverters
  with different isolated DC-link voltages of ratio
  equal to 10.366.
• With such a scheme it is found that all the 5th
  and 7th order (6n ? 1, where n 1,3,5,7 etc.)
  harmonics are absent in the motor phase voltage.
• The third harmonic order currents are eliminated
  from the motor by using isolated DC-link supply
  for the two inverters.
• A smooth transition to the over-modulation region
  is also achievable from the present open end
  winding IM drive.

101
Open-end winding IM drive
O
INVERTER - 2

• Open end winding circuit schematic
• Inverter 1 DC-link voltage is VDC
• Inverter 2 DC-link voltage is Vdc
• VDC 0.366 Vdc

102
Voltage space phasor diagrams of individual
inverters
3 (--)
2 (-)
2(-)
3(--)
1 (--)
0.366 VDC
4(-)
1(--)
VDC
4 (-)
6(-)
5(--)
Vector diagram inverter 2 Vector magnitude Vdc
5 (--)
6 (-)
Vector diagram inverter 1 Vector magnitude VDC
103
1,1 ? (--) 2,2 ? (-) 3,3 ? (--) 4,4
? (-) 5,5 ? (--) 6,6 ? (-) 7,7 ?
() 8,8 ? (---)
6
5
4
1
2
3
30?
6
5
1
4
3
2
30?
5
6
1
4
3
2
1.223 VDC
150
450
VDC
1200 k VDC

• Selected combinations of the vector
  positions from inverter 1 and inverter 2
  and calculation of DC link voltage ratio (k)
  for both the inverters.

VDC sin150 k VDC sin450 So k sin150 /
sin450 0.366
104
Relative position of different harmonics (1st to
13th ) of the motor phase from both inverter 1
and inverter 2
(c) 7th Harmonics
(b) 5th Harmonics
(a) - Fundamental
(e) 13th Harmonics
(d) 11th Harmonics
105
Relative position of different harmonics (17th
to 25th ) of the motor phase from both inverter
1 and inverter 2
(g) 19th Harmonics
(f) 17th Harmonics
Ref. point
(i) 25th Harmonics
(h) 23rd Harmonics
106
360
300
180
120
240
60
0
1
6
6
5
5
4
3
3
2
2
1
4
I
1
VAO
VBO
? ?t
VCO

• Switching vectors and pole voltage (VAO ,
  VBO , VCO ) of inverter-1

0
60
360
300
180
120
240
II
3
4
2
3
1
5
3
4
6
1
5
6
2
VAO
VBO
? ?t
VCO

• Switching vectors and pole voltage (VAO ,
  VBO , VCO ) of inverter - 2

107
EXPERIMENTAL RESULTS

• OVER MODULATION
• Phase voltage
• Harmonic spectrum
• Phase current
• Phase current and Fourier spectrum
• show absence of all 6n1 (n 1,3,5 .. etc)
  harmonics

Y-
axis 75v/div


Y-
axis 1 amp/div
108
EXPERIMENTAL RESULTS
a b c d

• MODULATING WAVE,TRIANGLE CARRIER WAVE AND
  CORRESPONDING GATE SIGNAL
• a Modulating wave and
• triangle carrier wave
• (inverter-1).
• b Inverter-1 pole
• voltage.
• c Modulating wave and
• triangle carrier wave
• (inverter-2).
• d Inverter-2 pole
• voltage (fc 6f)
•  

Phase-A and A
a b c d
Phase-B and B
a b c d
Phase-C and C
109
EXPERIMENTAL RESULTS

• MODULATION INDEX
• LESS THAN ONE (fc 6f)
• PHASE VOLTAGE
• FOURIER SPECTRUM
• PHASE CURRENT
• The Fourier spectrum shows increase
• in harmonic contents compared to
• that of over-modulation case.

Y axis 100v/div
Y-axis 1 amp/div
110
EXPERIMENTAL RESULTS

• MODULATION INDEX 0.45
• (fc 12f)
• PHASE VOLTAGE
• FOURIER SPECTRUM
• PHASE CURRENT
• The Fourier spectrum shows increase
• in 23rd and 25th harmonic contents.

Y-axis 100v/div



Y-axis 1 amp/div
111
THE RELATIVE RATIO OF DIFFERENT HARMONICS
GENERATED BY TRIANGULAR CARRIER AT DIFFERENT
MODULATION INDICES fc 6f
Fundamental
11th
25th
23rd
13th
112
THE RELATIVE RATIO OF DIFFERENT HARMONICS
GENERATED BY TRIANGULAR CARRIER AT DIFFERENT
MODULATION INDICES fc 12f
Fundamental
23rd
??? 11th , ??? 13th
25th
113
THE RELATIVE RATIO OF DIFFERENT HARMONICS
GENERATED BY TRIANGULAR CARRIER AT DIFFERENT
MODULATION INDICES fc 24f
fundamental
11th , 13th ooo 23rd , xxx 25th
114
THE RELATIVE RATIO OF DIFFERENT HARMONICS
GENERATED BY TRIANGULAR CARRIER AT DIFFERENT
MODULATION INDEX fc 24f
fundamental
fundamental
47th
37th , 39th
49th
115
CONCLUSION SALIENT FEATURES

• All the 6n ? 1, n 1, 3, 5 etc,. order
  harmonics are eliminated from the motor phase
  voltage in the entire speed range.
• A linear transition to the maximum modulation is
  possible.
•  By properly choosing the frequency modulation
  ratio (6, 12, 24, 48) at different speed ranges,
  the switching frequency of both inverters can
  be controlled within 500hz.
•  
• In the extreme speed range the lower voltage
  inverter is switched more frequently than the
  higher voltage inverter.
• The 11th and 13th order harmonic voltage
  amplitudes in the motor phase voltage can be
  suppressed by introducing notches in the
  modulating wave.
• The resultant fundamental is reduced to 99.57. 
• The resultant 11th order harmonic is reduced to
  50.  And the 13th order harmonic is reduced to
  31.86.

116
EXPERIMENTAL RESULTS 11th and 13th suppression
Modulating wave and triangular carrier wave (over
modulation ) fc/f 12
a Modulating wave (11th and 13th harmonics
suppressed) and triangle carrier wave
(inverter-1) b Inverter-1 pole voltage c
Modulating wave (11th and 13th harmonics
suppressed) and triangle carrier wave
(inverter-2) d Inverter-2 pole voltage
Pole voltage of inverter-1 ( Over modulation)
Pole voltage of inverter-2 ( Over modulation)
117
EXPERIMENTAL RESULTSPHASE VOLTAGE,FOURIER
SPECTRUM,PHASE CURRENTS(m gt 1)
Modulation index 1.0 Over-modulation. Phase
voltage with 11th and 13th suppressed. Y-axis
75v/div X-axis 5ms/div
Modulation index 1.0 Over-modulation Fourier
spectrum With 11th and 13th suppressed.
Modulation index 1.0 Phase current during
overmodulation.(No load operation with 11th and
13th suppressed) Y-axis 1A/div X-axis 5ms/div
118
EXPERIMENTAL RESULTSPHASE VOLTAGE,FOURIER
SPECTRUM,PHASE CURRENTS(m gt 0.9)
Modulation index 0.9. Phase voltage. fc 12f,
With 11th and 13th suppressed. Y-axis 75v/div
X-axis 5ms/div
Modulation index 0.9. fourier spectrum. fc
12f. With 11th and 13th suppressed
Modulation index 0.9. Phase current waveform.
fc 12f ( no load operation with 11th and 13th
suppressed). Y-axis 1A/div X-axis 5ms/div
119
EXPERIMENTAL RESULTSPHASE VOLTAGE,FOURIER
SPECTRUM,PHASE CURRENTS(m gt 0.45)
Modulation index 0.45. Phase voltage. fc 12f.
With 11th and 13th suppressed. Y-axis
75v/div X-axis 5ms/div
Y-
axis 75v/div
Modulation index 0.45. Fourier spectrum. fc
12f. With 11th and 13th suppressed
Modulation index 0.45. Phase current waveform.
fc 12f ( no load operation with 11th and 13th
suppressed). Y-axis 1A/div X-axis 10ms/div
Y-
axis 1A/div
120
HARMONIC ANALYSISRATIO OF DIFFERENT HARMONICS
VERSES MODULATION INDEX
fundamental
11th , 13th ooo 23rd , xxx 25th
fc 24f
fc 12f
fc 48f
121
A Novel Modulation Scheme for a Six Phase
Induction Motor with Open-End Windings
122
Winding disposition of a six-phase machine

• Six phase (split phase)motor configuration is
  achieved by splitting the phase belt of a
  conventional 3-phase induction motor into two
  halves namely abc and abc.
• The phase separation between a and a, b and b
  and c and c is 30

123
Inverter fed six-phase IM drive

• For a six phase induction motor drive harmonics
  of the order 6n ?1( n1,3,5 etc.,) will not
  contribute to the air gap flux.
• All these 6n ?1 ( n1,3,5 etc.,) order harmonic
  currents are limited by the stator impedance only
  and hence contribute to large harmonic currents.

124
Winding disposition of a six-phase machine

• The phase voltages and currents in a six phase
  motor can be represented by a six dimensional
  vector.
• By proper transformation three different
  sub-spaces can be generated which correspond to
  three different set of harmonic orders.
• The generalised vector used for the
  transformation matrix is Sk(a) cos k(a)
  cos k(a-?) cos k(a-9?).

125

• By putting a 0 and p/2, and ? equals to
  multiples of 30º in the generalised vector a
  transformation matrix is obtained.
• ? angular space separation between the two
  sets of 3-phase windings.

126

• The harmonics of order 6n?1 ( n 0, 2,4 etc.,)
  span a 2-dimesional subspace s1.
• The harmonics of order 6n?1 ( n 1, 3,5 etc.,)
  span a 2-dimesional subspace s2.
• The triplen order harmonics span a 2-dimesional
  subspace s3.
• They are orthogonal to each other.

127
Switching vectors in sub-space S1

• All switching vectors projected on
  subspaceS1 generates 6n?1 ( n 0, 2,4
  etc.,) harmonics.

128
Switching vectors in sub-space S2

• All switching vectors projected on
  subspaceS2 generates 6n?1 ( n 1, 3,5 etc.,)
  harmonics

129
Power schematic to suppress the 6n?1 ( n 1,3,5
etc.,) harmonics

• In the proposed scheme a modulation technique is
  used to eliminate all the 6n?1 ( n 1,3,5 etc.,)
  harmonics from the stator phases .
• An open-end winding drive configuration with
  DC-link voltages chosen in a ratio of 10.366
  will eliminate 6n?1 ( n 1,3,5 etc.,)
  harmonics.

130
Inverter vector selection to suppress the 6n?1 (
n 1,3,5 etc.,) harmonics

• From one side of open-end winding
• (inverter-1 and inverter-4) 11,21, 22,
  32,33,43,44,54,,55,65,66 and 16 vectors
  are switched.
• From the opposite side (inverter-2 and
  inverter-3) vectors 53, 45, 64, 56, 15,
  61, 26, 12, 31, 23, 42, and 34 are
  switched.

131
Inverter vector selection to suppress the 6n?1 (
n 1,3,5 etc.,) harmonics contd.

• Vectors 11 and 53 get added in S1 plane
• With DC-link voltage ratio of 11 / 53
  0.366 combined vectors on S2 plane are
  cancelled implying all 6n?1 ( n 1,3,5 etc.,)
  harmonic elimination .

132

• With DC-link voltage ratio of 0.366 12-sided
  polygonal voltage space phasor combinations are
  achieved for each 3-phase groups independently.
• A modulation scheme based on 12-sided polygonal
  voltage space phasors will cancel the 6n?1 ( n
  1,3,5 etc.,) harmonics voltage from all the motor
  phases.

133
Experimental results

• Phase voltage
• Harmonic spectrum
• Phase currents.
• 6n?1 ( n 1,3,5 etc.,) harmonics are absent.

134

• To suppress the 11th and 13th order harmonics in
  motor phases additional notches of 3.75 are
  provided in the modulation voltage.
• This results in a reduction of 11th harmonic to
  50 ,13th harmonic to 31.86 and fundamental to
  99.57 in magnitude.

135
Experimental results(with notch)

• Phase voltage
• Harmonic spectrum
• Reduction in 11th and 13th order harmonic
  magnitude.
• Phase currents.

136
Experimental results(with notch) Modulation
ratio of 12.

• Phase voltage
• Phase currents

137
Experimental results(with notch) Modulation
ratio of 24

• Phase voltage
• Phase currents

I

A
138
Experimental results(with notch) Modulation ratio
of 48

• Phase voltage
• Phase currents

139
Conclusion salient features

• A modulation technique to eliminate the 6n ?1 (
  n1,3,5 etc.,) harmonic currents, without the
  need for harmonic filters, from the stator
  phases of a six phase induction motor drive is
  explained.
• By appropriately choosing the frequency ratio
  between 12,24 and 48 for different speed ranges
  the inverter switching frequency can be limited
  to 600 hz .
• The proposed scheme used 4 inverters with a
  DC-link voltage of 0.41VDC and 0.15VDC , where
  VDC is the DC-link voltage of a 2-level 3-phase
  inverter, if the six-phase machine is run as a
  conventional 3-phase machine.

140
INDEPENDENT SPEED CONTROL OF TWO SIX PHASE
INDUCTION MOTORS USING A SINGLE
SIX PHASE INVERTER
141
Introduction

• A method of independent speed control of two
  induction motors from a single six-phase inverter
  is proposed.
• The positive sequence component consists of all
  the 12n ? 1 (n 0,1,2, .etc.) order harmonics.
• One of the two zero sequence components consists
  of all the 6n ? 1 (n 1,3,5 .etc.) order
  harmonics .

142
Inverter fed six-phase IM drive

• A six phase induction motor driven from six phase
  inverter
• Vas,Vbs,Vcs are the phase voltages of the a,b,c
  three phase group
• Vas,Vbs,Vcs are the phase voltages of the
  a,b,c three phase group

143

• Vas, Vbs, Vcs for a,b,c group.
• Vas, Vbs, Vcs for a,b,c
  group.
• Va, Vß Harmonics spanning subspace S1
• 12n ?1 (n 0,1,2,3 .etc.,)
• V1, V2 Harmonics spanning subspace S2
• 6n ? 1 (n 1,3,5 order .etc.,)
• Vo1, Vo2 Harmonics spanning subspace S3
  triplen harmonic

144
Stator Voltage equation
is input stator current vectors,
is input voltage vectors,
is input stator current vectors,
is stator resistance matrix,
is stator self inductance matrix,
is stator to rotor mutual inductance matrix.
145
Applying the orthogonal transformation to the
stator voltage equation
146
are two orthogonal components of stator currents
spanning subspace S1 ,
are two orthogonal components of stator currents
spanning subspace S2 ,
are the two orthogonal components of rotor
currents spanning subspace S1 ,
are two orthogonal components of rotor currents
spanning subspace S2 .
147
Rotor voltage equation
is stator resistance matrix,
is stator self inductance matrix,
is rotor to stator mutual inductance matrix.
148

• By applying the orthogonal transformation to
• the rotor voltage equation

149

• The corresponding voltage equations of stator
• and rotor spanning subspaces S1 and S2 can
  be
• separated out

Subspaces S1 .
Subspaces S2 .
150

• Only the positive sequence components traversing
  subspace S1 contribute for the air gap flux and
  electromagnetic torque production in machine.
• The zero sequence components do not contribute
  towards air gap flux production with the existing
  winding disposition.

151

• A scheme is proposed where the zero sequence
  components corresponding to the 6n ? 1 (n
  1,3,5 .etc.) order harmonics are impressed
  across a second six phase motor in proper phase
  sequence.
• The zero sequence components acts as positive
  sequence component for the second motor and hence
  develop air gap flux and electromagnetic torque
  in the second motor.

152
Six-phase IM winding disposition- S2 subspace
components produce torque
Stator schematic of the reconfigured six phase
induction machine ( voltage components in the S2
plane create air gap flux and torque)
153
Stator Voltage equation
is input stator current vectors,
is input voltage vectors,
is input stator current vectors,
is stator resistance matrix,
is stator self inductance matrix,
is stator to rotor mutual inductance matrix.
154
By applying the orthogonal transformation to the
stator voltage equation
155
Rotor Voltage equation
is stator resistance matrix,
is stator self inductance matrix,
is rotor to stator mutual inductance matrix.
156

• By applying the orthogonal transformation to
• the rotor voltage equation

157

• The corresponding voltage equations of stator
• and rotor spanning subspaces S1 and S2 can
  be
• separated out

Subspaces S1 .
Subspaces S2 .
158

• Only the harmonic components traversing subspace
  S2 contribute for the air gap flux and
  electromagnetic torque production in machine.
• The the harmonic components traversing subspace
  S1 do not contribute towards air gap flux
  production with the existing winding disposition.
  

159

• The 5th harmonic voltage, which spans the
  subspace S2 is represented by

• The 7th harmonic voltage, which spans the
  subspace S2 is represented by

• The phase relationship among the elements of
  the vector represented by 5th
• harmonic and 7th harmonic are similar except
  that the frequencies are
• different.

• Hence if the frequency and
  in the equations are replaced
• by , then a vector corresponding to
  the fundamental frequency
• spanning the subspace can be obtained.

160

• This orthogonal property is made use of for
  controlling two split-phase induction motors
  independently by connecting them in series and
  controlling with a single six-phase inverter.
• The reference modulating signals for the whole
  drive system are generated by superimposing the
  reference signals belonging to the subspace S1
  and the reference signals belonging to the
  subspace S2.

161
Schematic of the stator phase windings of the
two series connected six phase induction motors
162
Motor-1 phase voltage generation
Motor-2 phase voltage generation
Motor-1 and motor-2 combined phase voltage
generation
163
Control blocks for series connected six phase
motor drive
164
Experimental results
Reference voltage of phase-a of motor-1 and
motor-2 and the their combined voltage for PWM
generation (Motor-1 is running at 1000rpm(18Hz)
and motor-2 is running at 250rpm(9hz) . The
motors are running in opposite direction). No -
load operation. X- axis 50ms/div. Y- axis
200mv/div.
Reference voltage of phase-a of motor-1 and
motor-2 and the their combined voltage for PWM
generation (Motor-1 is running at 1000rpm(18 Hz)
and motor-2 is running at 250rpm(9 Hz) . The
motors are running in opposite direction). No -
load operation. X- axis 50ms/div. Y- axis
200mv/div.
Voltage waveform of phase-a and phase-a of
motor-2 (Motor-1 is running at 1000rpm(18hz) and
motor-2 is running at 250rpm(9hz) . The motors
are running in opposite direction).No - load
operation. X- axis 20ms/div. Y- axis 20v/div.
Voltage waveform of phase-a and phase-a of
motor-1 (Motor-1is running at 1000rpm(18Hz) and
motor-2 is running at 250rpm(9Hz) .The motors are
running in opposite direction). No - load
operation. X- axis 10ms/div. Y- axis 50v/div
165
Experimental results
Combined phase-a voltage waveform (Motor-1 is
running at 1000rpm(18hz) and motor-2 is running
at 250rpm(9hz) .The motors are running in
opposite direction). X- axis 10ms/div. Y- axis
50v/div.
Combined phase-a voltage waveform (Motor-1is
running at 1000rpm(18hz) and motor-2 is running
at 250rpm(9hz) .The motors are running in
opposite direction). X- axis 10ms/div. Y- axis
50v/div.
Current waveform of phase-a and phase-a
(Motor-1 is running at 1000rpm(18hz ) and motor-2
is running at 250rpm(9hz) . The motors are
running in opposite direction).No - load
operation. X- axis 50ms/div. Y- axis 1A/div.
Harmonic spectrum of current waveform in phase-a
(Motor-1 is running at 1000rpm(18hz) and motor-2
is running at 250rpm(9hz) . The motors are
running in opposite direction). Along normalised
frequency axis 9hz 1unit.
166
Experimental results
Voltage waveform of phase-a and phase-a of
motor-2 (Motor-1 is running at 1000rpm(18hz) and
motor-2 is running at 500rpm(18hz) .The motors
are running in same direction). X- axis 10ms/div.
Y- axis 20v/div.
Voltage waveform of phase-a and phase-a of
motor-1 (Motor-1is running at 1000rpm(18hz) and
motor-2 is running at 500rpm(18hz) .The motors
are running in same direction). X- axis 10ms/div.
Y- axis 50v/div.
Combined phase-a voltage waveform VA1N2 of
Fig.4b (Motor-1is running at 1000rpm(18hz) and
motor-2 is running at 500rpm(18hz) .The motors
are running in same direction). X- axis 10ms/div.
Y- axis 50v/div.
Combined phase-a voltage waveform VA1A2 of
Fig.4b (Motor-1is running at 1000rpm(18hz) and
motor-2 is running at 500rpm(18hz) .The motors
are running in same direction). X- axis 10ms/div.
Y- axis 50v/div.
167
Experimental results
Current waveform of phase-a and phase-a
(Motor-1 is running at 1000rpm(18hz) and motor-2
is running at 500rpm(18hz) .The motors are
running in same direction). X- axis 50ms/div. Y-
axis 1A/div. No-load operation.
Voltage waveform of phase-a and phase-a of
motor1 (Motor-1 is running at 1000rpm(18hz) and
motor-2 is stalled ). X- axis 10ms/div. Y- axis
50v/div.
Voltage waveform of phase-a and phase-a of
motor2 (Motor-1is running at 1000rpm(18hz) and
motor-2 is stalled ). X- axis 10ms/div. Y- axis
50v/div.
168
Experimental results
Combined phase-a voltage waveform VA1A2 of
Fig.4b (Motor-1 is running at 1000rpm(18hz) and
motor-2 is stalled). X- axis 10ms/div. Y- axis
50v/div.
Combined phase-a voltage waveform VA1N2 of
Fig.4b (Motor-1 is running at 1000rpm(18hz) and
motor-2 is stalled). X- axis 10ms/div. Y- axis
50v/div.
Current waveform of phase-a and phase-a
(Motor-1 is running at 1000rpm(18hz) and motor-2
is stalled ). X- axis 10ms/div. Y- axis 2mv/div.
No-load operation.
169
Experimental results
Current waveform of phase-a and speed of motor-2
(Motor-1 is making speed reversal from 1000rpm
to 1000rpm and motor-2 making speed reversal
from -250rpm to 250rpm ). X- axis 5s/div. Y-
axis 4A/div (current), 125rpm/div (speed)
Current waveform of phase-a and speed of motor-1
(Motor-1 is making speed reversal from 1000rpm
to 1000rpm and motor-2 making speed reversal
from -250rpm to 250rpm ). X- axis 5s/div. Y-
axis 4A/div (current), 500rpm/div (speed)
Current waveform of phase-a and speed of motor-2
(Motor-1 is making speed reversal from -1000rpm
to 1000rpm and motor-2 is running at constant
speed at 250rpm ). X- axis 5s/div. Y- axis
1A/div (current), 125rpm/div (speed)
Current waveform of phase-a and speed of motor-1
(Motor-1 is making speed reversal from -1000rpm
to 1000rpm and motor-2 is running at constant
speed at 250rpm ). X- axis 5s/div. Y- axis
1A/div (current), 500rpm/div (speed)
170
Experimental results
Current waveform of phase-a and speed of motor-2
(Motor-1 is running at constant speed of 1000rpm
and motor-2 is making speed reversal from
-250rpm to 250rpm ). X- axis 5s/div. Y- axis
1A/div (current), 250rpm/div (speed)
Current waveform of phase-a and speed of motor-2
(Motor-1 is running at constant speed of 1000rpm
and motor-2 is making speed reversal from
-250rpm to 250rpm ). X- axis 5s/div. Y- axis
1A/div (current), 125rpm/div (speed)
Voltage waveform of phase-a of motor-1 and
motor-2 (Motor-1 running at six step mode and
motor-2 is stalled ). X- axis 10ms/div. Y- axis
100v/div.
Current waveform of phase-a and phase-a
(Motor-1 running at six step mode and motor-2 is
stalled ). X- axis 20ms/div. Y- axis 1A/div
171
Experimental results
Harmonic spectrum of voltage waveform in phase-a
of motor-1 (Motor-1 is running in over modulation
(12 step) and motor-2 is stalled).
Harmonic spectrum of voltage waveform in phase-a
of motor-2 (Motor-1 is running in over modulation
(12 step) and motor-2 is stalled).
Current waveform of phase-a and phase-a
(Motor-1 is stalled and motor-2 is running at six
step mode). X- axis 20ms/div. Y- axis 1A/div
Voltage waveform of phase-a of motor-1 and
motor-2 (Motor-1 is stalled and motor-2 is
running at six step mode). X- axis 10ms/div. Y-
axis 100v/div.
172
Conclusion salient features

• A de-coupled speed control of two split phase
  (six phase) induction motor, from a single six
  phase inverter system is presented.
• In normal six phase motor the phase voltages
  corresponding to the 6n ? 1 (n 1,3,5 .etc.,)
  harmonic orders do not create torque and air gap
  flux.
• But the phase voltages corresponding to the 6n
  ? 1(n 1,3,5 .etc.,) harmonic orders when
  applied to another six phase motor in proper
  phase sequence , torque and air gap flux are
  created.
• Thus by the proper series connections of
  phases of the two six phase motors, the two
  motors can be run independently from a single six
  phase inverter.
• Independent speed control of the two motors are
  possible without the need for costly and bulky
  harmonic filters to suppress the high amplitude
  6n ? 1 (n 1,3,5 .etc.,) order zero sequence
  harmonic current components.

173
Independent Field Oriented Control Of Two
Split-phase Induction Motors From A Single
Six-phase Inverter
174
Terminal connection of the two series connected
split-phase (six-phase) induction motors.
175













176
Torque currents of motors
177
simultaneous speed reversal of motors ( motor-1(
Bottom trace) 500rpm to 500rpm and motor-2 (
Top Trace) -300rpm to 300rpm
178
Torque currents of motor-1 ( Bottom Trace) and
motor-2 (Top Trace)
179
Motor-1 is accelerating and motor-2is running at
constant speed
180
Motor-1 is doing speed reversal and Motor-2 is
at constant speed operation
181
(No Transcript)
182

• Independent speed control of the two motors
  are possible without the need for costly and
  bulky harmonic filters to suppress the high
  amplitude 6n ? 1 (n 1,3,5 .etc.,) order zero
  sequence harmonic current components.

183
A SENSORLESS SPEED CONTROL FOR INDUCTION MOTORS
USING RIPPLE CURRENTS IN SPACE PHASOR BASED PWM
CONTROL
184
Introduction

• A new method to estimate speed of induction motor
  without shaft transducer is proposed.
• The motor phase current ripple is used for
  estimation of rotor flux position.
• Two different schemes are used for flux position
  estimation in two different regions, one in low
  speed region and the other in high speed region.
• The proposed method uses space vector modulation
  with constant switching frequency.

185

• Steady state equivalent circuit of induction
  motor in rotor reference frame.
• The back emf vector lags the rotor flux
  vector by 90

W
synchronous






186

• The stator equation is

187

• During the effective period Teff (T1 T2) both
  back emf vector and active vectors cause the
  ripple current to flow.
• During the zero vector period T0 only the back
  emf vector causes the ripple current to flow.

T
T





188
Flux position estimation in low speed region

• Two samples of current vectors are taken in T/2
  time period difference during the zero vector
  period.
• When the modulating frequency is less than 50
  of the base frequency the zero vector period T0
  is more than the the effective period Teff i.e.
  T0 is more than half of the switching period T/2
  and hence there is sufficient deviation in
  current vector during zero period T0 .

189
Flux position estimation in high speed region

• Three samples of current are taken at
• t 0, t T/2 and t T.
• Effective period Teff is more than T/2(half of
  the switching period).
• Ripple current dependent on the two consecutive
  active vectors and the back emf vector.
• The flux position is estimated by creation of a
  virtual short circuit i.e. by eliminating the
  effect of active vectors from the ripple current.

190

• When the reference vector position ? is within
  30 from the first active vector in any sector,
  i.e. 0 lt ? lt 30, the time period T1 for the
  first active vector, is greater than the time
  period T2 for the second active vector
• Three samples of current are taken at t
  0, t T/2 and t T

191

• When the reference vector position ? is more than
  30 from the first active vector in a sector
  i.e. 30 lt ? lt 60,the time period T1 for the
  first active vector is less than the time period
  T2 for the second active vector
• Three samples of current are taken at t 0,
  t T/2 and t T

192

• Considering one case when reference vector is in
  sector-1

q
When
lt 30 in sector
-
1 i.e. when
period is more than
period




q
When
gt 30 in sector
-
1
i.e. when
period is more than
period




193

• By plotting the current deviation vector due to
  active vectors in the first half of sampling
  period
• for all the sectors we get a
  hexagon distorted clockwise.
• By plotting the current deviation vector due to
  active vectors in the second half of sampling
  period
• for all the sectors we get a
  hexagon distorted anticlockwise.

b


-
c






-
a

a




c
-
b















b




-
c






-
a


a



c


-
b










194

• By extracting the fundamental components we get
  that , the fundamental component of
  lags by F from
• , the fundamental component of
  reference vector and , the
  fundamental component of leads by F
  from
• .
• F
  16.15.

f





195

• Hence

t
he fundamental components of
can be written as










The fundamental components of the curr
ent deviation


phasor contributed

by back emf
.



Similarly
the fundamental components
of
can be




written as





A high resolution band pass filter whose center
frequency is dynamically tuned to the
fundamental frequency, is used for extraction of
these fundamental components from the sampled
ripple currents .












196

• From the three equations the back emf position is
  found as
• The rotor flux position leads by 90 from the
  back emf position, hence it can be obtained by
  adding 90 to the position of back emf vector.
• A speed control scheme is implemented based on
  the estimated rotor flux position.

197
Block diagram of sensorless speed control scheme

198
Experimental Results

• Flux position at frequency equal to 10 hertz.
• Flux position at frequency equal to 30 hertz.

199

• Flux position at frequency equal to 40 hertz.
• Reference speed and estimated speed for speed
  reversal application. Speed scaling 800rpm/div

200

• Phase current and estimated speed for speed
  reversal application. Current scaling 5A/div,
  Speed scaling 800rpm/div.
• Speed reversal (zoomed).

201

• Torque current and estimated speed during
  acceleration. Current scaling 5A/div, Speed
  scaling 600rpm/div
•  
• Phase current and estimated speed during
  acceleration. Current scaling 5A/div, Speed
  scaling 600rpm/div

202
A Five-level Inverter Topology With
Common-mode Voltage Elimination for Induction
Motor Drives
203
Introduction

• A five-level inverter topology and the switching
  state
• selection strategy for the PWM control, is
  proposed.
• The proposed scheme completely eliminates the
• common-mode voltages in the entire modulation
  range of
• the induction motor drive.
• The proposed scheme is based on a dual
  five-level inverter
• fed open-end winding induction motor
  configuration.
• With the absence of common-mode voltage,
  associated
• problems, such as, shaft voltages, bearing
  currents, etc.,
• are also eliminated in the proposed drive.

204
One leg of the proposed five-level inverter
topology

• A five-level inverter topology is
• proposed.
• It is formed by cascading two
• conventional two-level inverters
• and a conventional three-level
• NPC inverter.
• It offers simple power-bus
• structure compared to the
• five-level NPC inverter.
• It needs only two power diodes
• per leg (pole).

205
Realization of the five different voltage levels
IGBT Gating Logic
1 ? ON, 0 ? OFF S11-S14, S21-S34,
S24-S31, and S41-S44 are complementary pairs of
switches
206
Requirement of blocking voltage capability of
devices

• The requirement of
• blocking voltage capability
• of individual device goes
• to as low as
• Vdc/8 for S11, S14, S41, and
• S44
• while, it is
• Vdc/5.33 (3xVdc/2x8)
• for S21, S34, S24, and
• S31
• in the proposed open-end
• winding IM drive.

207
Power schematic of the dual-five level inverter
fed IM drive
208
The nine-level voltage space phasor generation
using the dual five-level inverter fed open-end
winding IM

• Voltage space phasor of individual five-level
  inverters

Inverter-A
Inverter-A

• Machine phase voltage in terms of inverter pole
  voltages

• Combined voltage space phasor

209
Switching states and voltage space vector
locations of the individual five-level inverter
(Inv.-A or Inv.-A)
61 Voltage Vectors 96 Triangular Sectors 125
Switching States

• Shaded vectors and
• states generate zero
• common-mode
• voltage