Development of Bondgraph Models for Power Electronic Systems

1
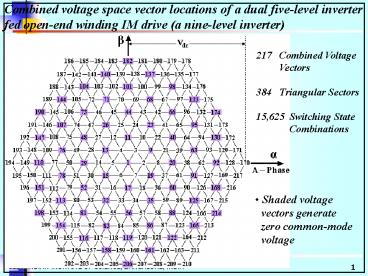
Combined voltage space vector locations of a dual
five-level inverter fed open-end winding IM drive
(a nine-level inverter)

• 217 Combined Voltage
• Vectors
• Triangular Sectors
• 15,625 Switching State
• Combinations

• Shaded voltage
• vectors generate
• zero common-mode
• voltage

2
Common-mode voltage of the dual five-level
inverter fed open-end winding IM drive

• Common-mode voltage generated by individual
  five-level inverters
• (Inverter-A or Inverter-A)

Inverter-A
Inverter-A

• Common-mode voltage in the phase voltage of
  induction motor with
• the proposed dual five-level inverter fed drive

3
Groups of common-mode voltage generated by
individual five-level inverter
Group Switching state of the five-level inverter (Inv.-A or Inv.-A) VCM
1 222 Vdc/4
2 122, 212, 221 5Vdc/24
3 022, 112, 121, 202, 211, 220 Vdc/6
4 012, 021, 102, 111, 120, 201, 210, 22-1, 2-12, -122 Vdc/8
5 002, 011, 020, 101, 110, 12-1, 1-12, 200, 21-1, 22-2, 2-11, 2-22, -112, -121, -222 Vdc/12
6 001, 010, 02-1, 0-12, 100, 11-1, 12-2, 1-11, 1-22, 20-1, 21-2, 2-10, 2-21, -102, -111, -120, -212, -221 Vdc/24
7 000, 01-1, 02-2, 0-11, 0-22, 10-1, 11-2, 1-10, 1-21, 20-2, 2-1-1, 2-20, -101, -110, -12-1, -1-12, -202, -211, -220 0
8 00-1, 01-2, 0-10, 0-21, 10-2, 1-1-1, 1-20, 2-1-2, 2-2-1, -100, -11-1, -12-2, -1-11, -1-22, -201, -210, -22-1, -2-12 -Vdc/24
9 00-2, 0-1-1, 0-20, 1-1-2, 1-2-1, 2-2-2, -10-1, -11-2, -1-10, -1-21, -200, -21-1, -22-2, -2-11, -2-22, -Vdc/12
10 0-1-2, 0-2-1, 1-2-2, -10-2, -1-1-1, -1-20, -20-1, -21-2, -2-10, -2-21 -Vdc/8
11 0-2-2, -1-1-2, -1-2-1, -20-2, -2-1-1, -2-20 -Vdc/6
12 -1-2-2, -2-1-2, -2-2-1 -5Vdc/24
13 -2-2-2 -Vdc/4
4
Voltage vectors and corresponding switching
states resulting into zero common-mode voltage in
individual five-level inverter (Inv.-A or
Inv.-A)
19 Voltage Vectors 24 Triangular Sectors 19
Switching States

• All the shaded switching
• states belong to the
• Group-7,which generate
• zero common-mode
• voltage at the inverter
• poles

5
Combined voltage space phasor locations
resulting into zero common-mode voltage (a
five-level inverter voltage space phasor
structure)
61 Combined Voltage Vectors 96
Triangular Sectors 361 Switching State
Combinations

• Achieved when individual
• five-level inverters (Inv.-A
• and Inv.-A) are switched
• using the switching states
• belonging to the Group-7
• only.

6
Number of redundant switching states available
for each voltage vectors of the five-level
inverter with zero common-mode voltage
61 Combined Voltage Vectors 96
Triangular Sectors 361 Switching Stats
Combinations

• Achieved when individual
• five-level inverters (Inv.-A
• and Inv.-A) are switched
• using the switching states
• belonging to the Group-7
• only.

7
Some of the voltage vectors and their redundant
switching states for five-level inverter with
zero common-mode voltage
Voltage Vector Redundant switching state combinations (switching state of Inverter-A, switching state of Inverter-A)
1 (000,000), (0-22,0-22), (1-21,1-21), (0-11,0-11), (1-10,1-10), (2-20,2-20), (11-2,11-2), (2-1-1,2-1-1), (-12-1,-12-1), (20-2,20-2), (-110,-110), (-211,-211), (-101,-101), (-202,-202), (-220,-220), (-1-12,-1-12), (02-2,02-2), (01-1,01-1), (10-1,10-1)
9 (000,-101), (0-11,-1-12), (02-2,-12-1), (11-2,01-1), (10-1,000), (1-21,0-22), (1-10,0-11), (2-1-1,1-10), (20-2,10-1), (2-20,1-21), (-110,-211), (-101,-202), (01-1,-110), (-12-1,-220)
11 (000,-202), (1-10,-1-12), (01-1,-211), (2-1-1,0-11), (02-2,-220), (11-2,-110), (20-2,000), (2-20,0-22), (10-1,-101)
28 (000,-1-12), (1-10,0-22), (01-1,-101), (2-1-1,1-21), (02-2,-110), (-12-1,-211), (11-2,000), (20-2,1-10), (-110,-202), (10-1,0-11)
95 (10-1,-202), (11-2,-211), (2-1-1,-1-12), (20-2,-101)
66 (01-1,-202), (02-2,-211), (10-1,-1-12), (11-2,-101), (20-2,0-11), (2-1-1,0-22)
174 (20-2,-202)
133 (11-2,-202), (20-2,-1-12)
98 (02-2,-202), (11-2,-1-12), (20-2,0-22)
8
Amplitude of maximum reference space vector
possible in linear range of modulation without
boost in the DC-link of the proposed inverter
9
Generation of same maximum peak fundamental
amplitude of the phase voltage equivalent to that
of a conventional SVPWM based five-level inverter

• A boost of 15 in the dc-link of the proposed
  drive is
• required to generate the maximum peak
  fundamental
• amplitude of the phase voltage equivalent to
  that of a
• conventional SVPWM based five-level inverter.

10
Voltage space vector locations for proposed
five-level inverter with common-mode voltage
elimination (with dc-link boost)
61 Combined Voltage Vectors 96
Triangular Sectors 361 Switching Stats
Combinations
11
Switching state combination selected to generate
the voltage space phasors of five-level inverter
with zero CMV
61 Combined Voltage Vectors 96
Triangular Sectors 61 Switching Stats
Combinations
12
Power scheme of the proposed five-level inverter
with CME
13
Experimental results
Pole voltage (VAO)
Two-level operation Y-axis 1 div. 50 V X-axis
1 div. 10 ms
Phase voltage (VAA)
Pole voltage (VAO)
Phase voltage FFT (two-level operation) Y-axis
Normalized amplitude X-axis Order of harmonic
Pole voltage FFT (two-level operation) Y-axis
Normalized amplitude X-axis Order of harmonic
14
Experimental results (contd)
Pole voltage (VAO)
Three-level operation Y-axis 1 div. 40
V X-axis 1 div. 10 ms
Phase voltage (VAA)
Pole voltage (VAO)
Phase voltage FFT (three-level operation) Y-axis
Normalized amplitude X-axis Order of harmonic
Pole voltage FFT (three-level operation) Y-axis
Normalized amplitude X-axis Order of harmonic
15
Experimental results (contd)
Pole voltage (VAO)
Four-level operation Y-axis 1 div. 70
V X-axis 1 div. 5 ms
Phase voltage (VAA)
Pole voltage (VAO)
Phase voltage FFT (four-level operation) Y-axis
Normalized amplitude X-axis Order of harmonic
Pole voltage FFT (four-level operation) Y-axis
Normalized amplitude X-axis Order of harmonic
16
Experimental results (contd)
Pole voltage (VAO)
Five-level operation Y-axis 1 div. 75
V X-axis 1 div. 5 ms
Phase voltage (VAA)
Pole voltage (VAO)
Phase voltage FFT (five-level operation) Y-axis
Normalized amplitude X-axis Order of harmonic
Pole voltage FFT (five-level operation) Y-axis
Normalized amplitude X-axis Order of harmonic
17
Experimental results (contd)
Pole voltage (VAO)
Over-modulation operation Y-axis 1 div. 80
V X-axis 1 div. 5 ms
Phase voltage (VAA)
Pole voltage (VAO)
Phase voltage FFT (over-modulation
operation) Y-axis Normalized amplitude X-axis
Order of harmonic
Pole voltage FFT (over-modulation
operation) Y-axis Normalized amplitude X-axis
Order of harmonic
18
Experimental results (contd)
Phase voltage (VAA) Y-axis 1 div. 50 V
Four-level operation X-axis 1 div. 5 ms
Phase current Y-axis 1 div. 1 A
Phase voltage (VAA) Y-axis 1 div. 50 V
Five-level operation X-axis 1 div. 5 ms
Phase current Y-axis 1 div. 1 A
19
Salient features of the proposed common-mode
elimination scheme for multilevel inverter fed
drive

•  A dual five-level inverter fed open-end winding
  induction motor
• drive with elimination of common-mode voltage
  in the entire
• operating range.
• Each five-level inverter of the proposed drive
  is formed by
• cascading two conventional two-level inverters
  and a conventional
• three-level NPC inverter. Hence, the proposed
  drive offers simple
• power-bus structure compared to the five-level
  NPC inverter fed
• drive.
• There is no alternating common-mode voltage in
  the inverter
• poles as well as at the phase windings of the
  induction machine.

20
Salient features of proposed common-mode
elimination scheme for multilevel inverter fed
drive (contd)

• A common DC-link is used at both the ends of the
  open-end
• winding induction machine, for both the
  five-level inverters.
• The DC-link voltage requirement of proposed
  open-end winding
• IM drive is nearly half as compared to that of
  a single five-level
• inverter fed conventional IM drive.
• Hence, the voltage stress on the devices is
  reduced and devices
• with lower voltage blocking capability can be
  used, which makes
• the proposed drive scheme suitable for high
  power applications.

21
CONCLUSION

• In the implemented scheme, the rotor flux
  position is estimated from the motor phase
  current ripples
• During the low speed region of operation, the
  current ripple during the zero vector periods are
  used for rotor flux position estimation
• During the high speed region of operation, the
  current ripple during the active vector periods
  are used for rotor flux position estimation
• The scheme is implemented for a three phase
  motor, but the scheme can be extended to any
  multi phase motor and also with open-end winding
  structure

22
Linearization of the Multi-level SVPWM in
Over-modulation Region
By R. S. Kanchan, P. N. Tekwani, and K.
Gopakumar Centre for Electronic Design and
Technology, Indian Institute of
Science Bangalore, INDIA
23
Linearization of the Multi-level SVPWM in the
Over-Modulation Region
Conventional two-level Sine-Triangle PWM
The fundamental component in the output PWM
waveform is equal to
k (peak amplitude of the sinusoidal reference)
/ (height of the triangular carrier signal)

• Three sinusoidal (1200 phase shifted) reference
  signals are compared with triangular carrier
• The PWM signals are generated for three phases
• The pole voltage is clamped to ve DC link bus
  if Vref gtVt else to ve DC link bus

24
Linearization of the Multi-level SVPWM in the
Over-Modulation Region
Conventional Sine-Triangle PWM Over-Modulation
Range

• When ref signal is greater than carrier, the
  pole voltages are clamped to the DC link bus
  voltage
• The fundamental component in output PWM waveform
  is not given by
• But there is reduction in the fundamental
  component in the output voltage

25
Linearization of the Multi-level SVPWM in the
Over-Modulation Region
Conventional Sine-Triangle PWM Over-Modulation
Range

• Reduction in the output fundamental is
  proportional to the shaded area

26
Linearization of the Multi-level SVPWM in the
Over-Modulation Region
Conventional Sine-Triangle PWM

• The voltage transfer characteristics i.e the
  ratio between the output fundamental and the
  reference signal amplitude is non-linear in the
  over-modulation region

27
Linearization of the Multi-level SVPWM in the
Over-Modulation Region
Carrier based Space-Vector PWM (SVPWM)

• The reference signals are added with an offset
  voffset1
• The resultant PWM is a Space Vector PWM

28
Linearization of the Multi-level SVPWM in the
Over-Modulation Region
Carrier based Space-Vector PWM (SVPWM)

• Again when ref signal is greater than carrier,
  the pole voltages are clamped to the DC link bus
  voltage
• There is reduction in the fundamental component
  in the output voltage
• Reduction in the output fundamental is
  proportional to the shaded area

29
Linearization of the Multi-level SVPWM in the
Over-Modulation Region

• The extended linear region in SVPWM as compared
  to SPWM
• The voltage transfer characteristics is again
  non-linear in the over-modulation region
  similar to SPWM

Ideal requirement for the PWM modulator Linear
voltage transfer characteristics
30
Linearization of the Multi-level SVPWM in the
Over-Modulation Region
In the Proposed Work

• An over-modulation scheme with the linear voltage
  transfer characteristics for a general n-level
  SVPWM signal generation
• Reference signal to the PWM modulator is
  pre-scaled in over-modulation region such that
• The fundamental component of the original and the
  modified reference signal is same
• The modified reference signal is always within
  carrier region
• Thus voltage transfer characteristic is a linear
  function of the modulation index both in the
  linear-modulation as well as in the
  over-modulation region
• The inverter leg switching times are directly
  obtained with a simple algorithm using only the
  sampled amplitudes of the reference phase voltages

31
Linearization of the Multi-level SVPWM in the
Over-Modulation Region
Principle of linearization when k0.637 i.e. six
step mode
k0.637

• F1, the original reference signal in six step
  mode ( f1 (pk)0.637) goes above the carrier
  (0.5)
• The output voltage will be less, if f1 is used
  for PWM generation
• f2 is a rectangular signal such that fundamental
  component of f2 is equal to f1, the original
  reference signal in six step mode i.e. F2
  (1)0.637
• Therefore, f2 can be used for PWM generation
  instead of f1

32
Linearization of the Multi-level SVPWM in the
Over-Modulation Region
Principle of linearization when 0.5 lt k lt 0.637

• A part of original reference signal is clamped
• The fundamental component of the modified
  reference signal is same as original reference
  signal

• This requires that the fundamental component of
  rectangular pulse f2 is equal to fundamental
  component of part of the original reference
  signal f1

33
Linearization of the Multi-level SVPWM in the
Over-Modulation Region

• Fundamental component of part of the original
  reference signal f1

• Fundamental component of rectangular pulse f2

34
Linearization of the Multi-level SVPWM in the
Over-Modulation Region

• The relationship between modulation index MI and
  clamping angle q

• Thus if MI is known, the clamping angle q can
  be determined
• The modified reference signal is clamped for the
  angle q to p-? and p? to 2p-?

35
Linearization of the Multi-level SVPWM in the
Over-Modulation Region
Principle of the proposed SVPWM in the
over-modulation region

• Modified reference signal

• Reference signal goes out of the carrier two
  times in the positive half cycle

36
Linearization of the Multi-level SVPWM in the
Over-Modulation Region
Principle of the proposed SVPWM in the
over-modulation region

• The reference signal is clamped to 0.5 twice in
  ve half cycle
• Again the fundamental component of the modified
  reference signal is same as original reference
  signal

37
Linearization of the Multi-level SVPWM in the
Over-Modulation Region
Principle of the proposed SVPWM in the
over-modulation

• The fundamental component of the original
  reference signal f1 between q to 2p/3-?

0.5
?0
(2p/3- ?)0

• The fundamental component of rectangular pulse f2
  between q to 2p/3-?

0
0.5

• For the fundamental component of the modified
  reference signal to be same as original signal,

?0
(2p/3- ?)0
0
p/3
wt
p/2
p/6
00
38
Linearization of the Multi-level SVPWM in the
Over-Modulation Region
Principle of the proposed SVPWM in the
over-modulation

• The relationship between modulation index MI and
  clamping angle q

• Thus if MI is known, the clamping angle ? can be
  determined

• Clamping of the modulating signal starts when

0.5
and clamping angle ? is equal to p/3

• When clamping angle p/6, k 0.60337

• Thus the clamping scheme can be used only in the
  range 0.577ltk lt0.60337 as the clamping starts at
  an angle less than p/6, where modulating wave is
  (3/2)ksin(wt) instead of

?0
This is referred as over-modulation Mode-I
(0.577ltk lt0.60337)
(2p/3- ?)0
0
p/3
p/6
p/2
wt
00
39
Linearization of the Multi-level SVPWM in the
Over-Modulation Region
Principle of the proposed SVPWM in the
over-modulation MODE-II

• The reference signal is clamped to 0.5 for ? lt wt
  lt p- ?
• Again the fundamental component of the modified
  reference signal is same as original reference
  signal (dotted line)

• The MI range greater than 0.60337, angle ? at
  which clamping starts is less than p/3

.
0.5
?0
(p -?)0
0
p
p/3
p/2
p/6
2p/3
wt
00
40
Linearization of the Multi-level SVPWM in the
Over-Modulation Region
Principle of the proposed SVPWM in the
over-modulation MODE-II

• The relationship between ? and k can be derived
  similarly

41
Linearization of the Multi-level SVPWM in the
Over-Modulation Region
Principle of the proposed SVPWM in the
over-modulation MODE-II
Summary The relationship between ? and k

• Over-modulation Mode-I (0.577ltk lt0.60337)
  clamping angle p/3lt?lt p/6

• Over-modulation Mode-II (0.60337ltk lt0.637)
  clamping angle 0lt?lt p/3

42
Linearization of the Multi-level SVPWM in the
Over-Modulation Region
The relationship between ? and k (MI) for SPWM
and SVPWM

• Steps
• Read Modulation Index MI
• Determine clamping angle ?
• Clamp the reference signal to 0.5 appropriately
• The implementation needs instantaneous angle
  information

43
Space Vector PWM signal generation for
multi-level inverters using only the sampled
amplitudes of reference phase voltages
Modified reference voltages and triangular
carriers for a five-level SVPWM scheme

• n-level SPWM scheme uses n-1 level shifted
  carrier waves
• Sinusoidal reference signals are added with
  offset which centers them within carrier region

44
Space Vector PWM signal generation for
multi-level inverters using only the sampled
amplitudes of reference phase voltages
Determination of the Ta_cross , Tb_cross and
Tc_cross during switching interval TS (When
reference voltages are spanning the inner carrier
region, MI lt 0.433)
Ta_cross , Tb_cross and Tc_cross the time
duration from the start of switching interval
when the reference phase - A, B and C cross the
carrier
45
Space Vector PWM signal generation for
multi-level inverters using only the sampled
amplitudes of reference phase voltages
Determination of the Ta_cross , Tb_cross and
Tc_cross during switching interval TS (When
reference voltages are spanning the inner carrier
region, MI lt 0.433)
Carrier- C1
Carrier- C2
Carrier- C2
Tas , Tbs and Tcs Time equivalents of the
modified reference signal amplitudes
46
Space Vector PWM signal generation for
multi-level inverters using only the sampled
amplitudes of reference phase voltages
Determination of the Ta_cross , Tb_cross and
Tc_cross during switching interval TS (When
reference voltages are spanning the entire
carrier region, 0.433ltMI lt 0.866)
47
Space Vector PWM signal generation for
multi-level inverters using only the sampled
amplitudes of reference phase voltages
SUMMARY Ta_cross , Tb_cross and Tc_cross for
various carrier regions to bring the reference
within a carrier region
48
Space Vector PWM signal generation for
multi-level inverters using only the sampled
amplitudes of reference phase voltages
Determination of the Ta_cross Represent the
carriers and ref. signals in terms of time
equivalents using relationship
49
Space Vector PWM signal generation for
multi-level inverters using only the sampled
amplitudes of reference phase voltages
Determination of the Ta_cross Shift the ref.
signal into one carrier region (first ve
carrier) by adding proper offset

50
Space Vector PWM signal generation for
multi-level inverters using only the sampled
amplitudes of reference phase voltages
Determination of the Ta_cross
51
Space Vector PWM signal generation for
multi-level inverters using only the sampled
amplitudes of reference phase voltages
Determination of the Ta_cross
52
Space Vector PWM signal generation for
multi-level inverters using only the sampled
amplitudes of reference phase voltages
Equivalence to Conventional SVPWM

• The reference signals in carrier based SVPWM are
  shifted to one carrier region
• The outer sub-hexagon in the conventional SVPWM
  are shifted to central sub-hexagon in
  conventional SVPWM
• The reference signal shifting in carrier based
  SVPWM is equivalent to sub-hexagonal shifting in
  the conventional SVPWM

53
Space Vector PWM signal generation for
multi-level inverters using only the sampled
amplitudes of reference phase voltages
Algorithm for inverter leg switching time
calculation Tfirst_cross , Tsecond_cross and
Tthird_cross the time duration from the start
of switching interval when the reference phases
cross the carrier for first, second and third
time respectively.
, x a, b, c
Inverter leg switching times
54
Space Vector PWM signal generation for
multi-level inverters using only the sampled
amplitudes of reference phase voltages
Tgfirst_cross , Tgsecond_cross and Tgthird_cross
the inverter leg switching time for the
reference phases which cross the carrier for
first, second and third time respectively.
The traces of Tgfirst_cross , Tgsecond_cross and
Tgthird_cross showing centered time duration for
middle vectors
55
Space Vector PWM signal generation for
multi-level inverters using only the sampled
amplitudes of reference phase voltages
56
Space Vector PWM signal generation for
multi-level inverters using only the sampled
amplitudes of reference phase voltages
Schematic representation of the Multi-level SVPWM
Inverter Gating Signals
PWM Compa- rators
Gating Signals Tgx
Ta_cross, Tb_cross Tc_cross
VAN
Time Equivalents Txs

VBN

VCN
Toffset1
Toffset2
57
Implementation of the Multi-level SVPWM with
Linear Transfer Characteristics in Over-Modulation
In overmodulation, clamps the reference signals
appropriately
MI
Vs
Inverter Gating Signals
PWM Compa- rators
Gating Signals Tgx
Ta_cross, Tb_cross Tc_cross
Pre- scaler
VAN

Time Equivalents Txs
VBN
Toffset2

VCN
Toffset1
58
Implementation of the Multi-level SVPWM with
Linear Transfer Characteristics in Over-Modulation

• Pre-scaler
• Read Modulation Index MI
• Determine clamping angle ? and then Clamping
  level A
• Clamp the reference signal if it is greater than
  A

59
Linearization of the Multi-level SVPWM in the
Over-Modulation Region

• The clamping angle information is converted into
  a level signal A

• Prescaler A simple look-up table of MI vs A

60
Simulation Results Linear-Modulation Region

• No clamping of Tas in linear range of modulation
• Pre-scaler is inactive in linear modulation range

(wt)
61
Simulation Results Over-Modulation Region (MI
0.92)

• Clamping of Tas in over-modulation (Mode-I)
• Pre-scaler is active in over-modulation range

62
Simulation Results Over-Modulation Region (MI
0.94)
63
Simulation Results Over-Modulation Region (MI
0.95)

• Clamping of Tas in over-modulation (Mode-II)
• Pre-scaler is active in over-modulation range

64
Simulation Results Over-Modulation Region (MI
0.96)
65
Simulation Results Over-Modulation Region (MI
0.98 )
66
Simulation Results Over-Modulation Region (MI
1.00)

• Square-wave switching mode

67
Experimental verification Five-level inverter
fed IM drive configuration
68
Five-level inverter fed IM drive configuration
Inverter-A

• Each three-level inverter configuration by
  cascading two two-level inverters
• The pole voltage can attain three levelsVdc/2, 0
  ,
• -Vdc/2

Ref V. T. Somasekhar, K. Gopakumar, Three -
level inverter configuration cascading two
2-level inverters, IEE Proc. EPA, Vol. 150,
No. 3, May 2003, pp.245-254
69
Five-level inverter fed IM drive configuration
Ref M. R. Baiju, K. K. Mohapatra, V. T.
Somasekhar, K. Gopakumar and L. Umanand, A
five-level inverter voltage space phasor
generation for an open-end winding induction
motor drive, IEE Proc. EPA, Vol. 150, No. 5,
Sept 2003, pp 531-538

• Five-level space phasor generation across
  induction motor windings Vdc/2,Vdc/4, 0 ,
  -Vdc/4, or -Vdc/2

70
Experimental Results The traces of pre-scaler
output Tas and inverter leg switching time Tga
Linear-Modulation Region (MI 0.906)
Tas
Tga
71
Experimental Results The traces of pre-scaler
output Tas and inverter leg switching time Tga
Over-Modulation Region (MI 0.92)
Tas
Tga
72
Experimental Results The traces of pre-scaler
output Tas and inverter leg switching time Tga
Over-Modulation Region (MI 0.94)
Tas
Tga
73
Experimental Results The traces of pre-scaler
output Tas and inverter leg switching time Tga
Over-Modulation Region (MI 0.96)
Tas
Tga
74
Experimental Results The traces of pre-scaler
output Tas and inverter leg switching time Tga
Over-Modulation Region (MI 0.98)
Tas
Tga
75
Experimental Results The traces of pre-scaler
output Tas and inverter leg switching time Tga
Square wave switching mode (MI 1.00)
Tas
Tga
76
Experimental Results The traces machine phase
voltage and inverter leg switching time Tga
Linear modulation region (MI 0.906)
Phase voltage
Tga
77
Experimental Results The traces machine phase
voltage and inverter leg switching time Tga
Over-Modulation Region (MI 0.926)
Phase voltage
Tga
78
Experimental Results The traces machine phase
voltage and inverter leg switching time Tga
Over-Modulation Region (MI 0.95)
Phase voltage
Tga
79
Experimental Results The traces machine phase
voltage and inverter leg switching time Tga
Over-Modulation Region (MI 0.97)
Phase voltage
Tga
80
Experimental Results The traces machine phase
voltage and inverter leg switching time Tga
Square wave switching mode (MI 1.00)
Phase voltage
Tga
81
Experimental Results The traces machine phase
voltage and phase current
Linear-Modulation Region (MI 0.906)
Phase voltage
Phase current
82
Experimental Results The traces machine phase
voltage and phase current
Linear-Modulation Region (MI 0.93)
Phase voltage
Phase current
83
Experimental Results The traces machine phase
voltage and phase current
Linear-Modulation Region (MI 0.957)
Phase voltage
Phase current
84
Experimental Results The traces machine phase
voltage and phase current
Linear-Modulation Region (MI 0.97)
Phase voltage
Phase current
85
Experimental Results The traces machine phase
voltage and phase current
Square wave switching mode (MI 1.00)
Phase voltage
Phase current
86
Experimental Results Transition from Linear to
square wave switching mode
Top Trace time equivalent of modified reference
signals Tas Bottom Trace Inverter gate
switching time Tga
87
Experimental Results Transition from Linear to
six-step mode
Top Trace Phase voltage, Bottom Trace Phase
current
88
Fundamental output voltage as a function of
modulation index-MI
89
Harmonic components in the output waveform in the
over-modulation region
90
Linearization of the Multi-level SVPWM in the
Over-Modulation Region
SUMMARY

• A simple n-level PWM signal generation with
  linear voltage transfer characteristics
  throughout the modulation range, up to six-step
  mode of operation
• Linear voltage transfer characteristics in the
  over-modulation region is achieved by modifying
  the reference signal such that
• the modified reference signal has the same
  fundamental component as the original reference
  signal
• modified reference signals are always within the
  carrier region
• Inverter leg switching times are directly
  obtained from the sampled amplitudes of reference
  phase voltages signals
• Does not require any sector identification, sine
  look-up tables for switching vector
  identification
• Does not use sector mapping or complex timing
  calculations

91
Twelve-sided polygonal voltage space vector based
multilevel inverter for induction motors.
92
Topology of a multilevel inverter for generation
of 12-side polygonal voltage space vectors for
induction motor drives.
93
Generation of voltage space vectors
94
(No Transcript)
95
Va positive Vb-Vc positive 1st quadrant
Va negative Vb-Vc positive 2nd quadrant
Va negative Vb-Vc negative 3rd quadrant
Va positive Vb-Vc negative 4th quadrant
96
If in quadrant 1 If Vb-VcltVa.v3.tan150 then
sector 1 else If Vb-VcltVa.v3.tan450
then sector 2 else If Vb-VcltVa.v3.tan750
then sector 3 else sector 4
If in quadrant 2 If Vb-VcltVa.v3.tan150 then
sector 7 else If Vb-VcltVa.v3.tan450 then
sector 6 else If Vb-VcltVa.v3.tan750 then
sector 5 else sector 4
97
If in quadrant 3 If Vb-VcltVa.v3.tan150 then
sector 7 else If Vb-VcltVa.v3.tan450 then
sector 8 else If Vb-VcltVa.v3.tan750 then
sector 9 else sector 10
If in quadrant 4 If Vb-VcltVa.v3.tan150 then
sector 1 else If Vb-VcltVa.v3.tan450 then
sector 12 else If Vb-VcltVa.v3.tan750 then
sector 11 else sector 10
98
V/f scheme for the drive
99
Comparison to obtain time durations
100
Pole voltage at 30Hz.

• Voltage levels at 0.366Vdc, 1.0Vdc and 1.366Vdc
  are observed.

101
Phase voltage at 30Hz.
102
Pole voltage at 50Hz.
103
Phase voltage at 50Hz.
104
Fig. 14a Phase voltage and motor current at
15Hz. (X-axis 1div20ms, Y-axis 1div100V)
Fig. 14b Pole voltage at 15Hz. (X-axis
1div20ms, Y-axis1div50V)
105
Fig. 15a Phase voltage and motor current at
30Hz. (X-axis 1div10ms, Y-axis 1div50V)
Fig. 15b Pole voltage and motor current at
30Hz. (X-axis 1div5ms, Y-axis 1div50V)
106
Fig. 16a Phase voltage and motor current at
45Hz. (X-axis 1div10ms, Y-axis 1div100V)
Fig. 16b Pole voltage at 45Hz. (X-axis
1div10ms, Y-axis 1div50V)
107
Fig. 17b Pole voltage at 50Hz. (X-axis
1div5ms, Y-axis1div50V)
Fig. 17a Phase voltage and motor current at
50Hz. (X-axis 1div5ms, Y-axis 1div100V)
108
Fig. 18 Harmonics at 15Hz operation. (X-axis
nth harmonic, Y-axis Relative amplitude)
109
Fig. 19 Harmonics in 30Hz operation. . (X-axis
nth harmonic, Y-axis Relative amplitude)
110
Fig. 20 Harmonics in 45Hz operation. (X-axis
nth harmonic, Y-axis Relative amplitude)
111
Fig. 21 Harmonics in 50Hz operation. . (X-axis
nth harmonic, Y-axis Relative amplitude)
112
Control of Switching
Frequency Variation in Hysteresis Controller for
IM Drives Using Variable Parabolic Bands for
Current Error Space Phasor
113
Problem of Switching Frequency Variation

• Common problems associated with the conventional,
  as well as current error space phasor based
  hysteresis controllers with fixed bands
  (boundaries), are the wide variation of switching
  frequency in a fundamental output cycle and
  variation of switching frequency with the
  variation in the speed of the load motor.
• These problems cause increased switching looses
  in the inverter, non-optimum current ripple, and
  excess harmonics in the load current, which leads
  to additional heating in the motor.

114
Two-Level VSI fed IM Drive
Voltage Space Phasor Structure
Power Schematic
115
Directions of Current Error Space Phasor When
Different Voltage Vectors are Switched for
Different Positions of Vm in Sector-1
Start of the Sector
Middle of the Sector
End of the Sector
116
Factors Influencing the Switching Frequency
Variation

• Leakage inductance of the machine (L?)
• Machine voltage vector (Vm) (dominated by the
  back emf vector Vb)
• DC-link voltage (as amplitude of Vk is decided by
  dc-link voltage)
• Current error space phasor ripple (?(?i))

117
Variation of Switching Frequency in Hysteresis
Current Controller

• Over a fundamental period, the position of Vm
  varies with respect to the inverter voltage
  vectors of space phasor structure.
• Also, the selected inverter voltage vector Vk
  (V1, , V8) keeps on changing in a fundamental
  cycle during hysteresis PWM current control.
• Therefore, either the inverter switching
  frequency or/and the current error space phasor
  ripple will vary over a fundamental inverter
  period.

118
Variation of Switching Frequency in
Hysteresis Current Controller (Contd)

• For the given operating speed, if the shape of
  the fixed boundary of the current error space
  phasor is not properly selected, the switching
  frequency of inverter will vary over a
  fundamental cycle.
• Further to this, if the same boundary of current
  error space phasor is maintained at different
  operating speeds of the machine (for different
  fundamental values of the machine back emf) then
  also the inverter switching frequency will vary.

119
Investigation of Current Error Space Phasor
in VC-SVPWM based VSI fed IM Drives
Typical SVPWM switching pattern of the
inverter voltage vectors for two
consecutive PWM switching intervals
120
Investigation of Current Error Space Phasor in
VC-SVPWM based VSI fed IM Drives (Contd)
Switching times for inverter voltage vectors in a
switching interval
121
Investigation of Current Error Space Phasor in
VC-SVPWM based VSI fed IM Drives (Contd)
Current error space phasor during switching of
various voltage vectors
Specific form for Sector-1
122
Movement of current error space phasor (on ?-?
plane) in a few sampling intervals of VC-SVPWM
based two-level VSI fed IM drive
Y-axis And X-axis Current In Amperes
Vm at middle of the sector (? varies from 27? to
33?)
Vm at start of the sector (? varies from 0? to
7?)
Vm at end of the sector (? varies from 54? to
60?)
123
Approximate theoretical boundary of ?i for
VC-SVPWM based two-level VSI fed IM drive for
position of Vm in Sector-1
Y-axis And X-axis Current In Amperes
10 Hz
20 Hz
40 Hz
30 Hz
124
Simulation results for VC-SVPWM based two-level
VSI fed IM drive
10 Hz Operation
125
Simulation results for VC-SVPWM based two-level
VSI fed IM drive
20 Hz Operation
126
Simulation results for VC-SVPWM based two-level
VSI fed IM drive
30 Hz Operation
127
Simulation results for VC-SVPWM based two-level
VSI fed IM drive
35 Hz Operation
128
Simulation results for VC-SVPWM based two-level
VSI fed IM drive
41 Hz Operation
129
Comparison of boundary obtained by theoretical
calculations and simulation studies for VC-SVPWM
based two-level VSI fed IM drive
Theoretical
10 Hz
20 Hz
30 Hz
40 Hz
0.1 A/div.
0.2 A/div.
0.2 A/div.
0.5 A/div.
Simulation
130
Establishing variable boundary for proposed
hysteresis controller
The parabola is defined as the locus of a point
which moves so that it is always at the same
distance from a fixed point (called the focus)
and a given line (called the directrix).

• Formula for a vertical parabola (having Y-axis as
  axis of symmetry) with the vertex on (h, k), is
  (x-h)24p(y-k).
• Formula for a horizontal parabola (having X-axis
  as axis of symmetry) with the vertex on (h, k),
  is (y-k)24p(x-h).
• Here, p is the distance between
• vertex and focus of the parabola.

131
Equivalent new X-axis and Y-axis for the
parabolas of current error space phasor boundary
in different sectors
Sectors X-axis Y-axis
1, 4 B-axis jB-axis
2, 5 A-axis jA-axis
3, 6 C-axis jC-axis
132
Generalized technique to find the parameters of
the boundary defining parabolas for given
induction motor
(x, y), (h, k), p For boundary defining
parabolas for operating frequency from 1 Hz to 45
Hz with the resolution of 1 Hz
Vdc, Base_freq, L?, TS,
Generalized Technique (Matlab Program) Developed
in Proposed Work
input
output
133
Boundary for proposed hysteresis controller with
new reference axis
134
Parameters of boundary defining parabolas for
proposed hysteresis controller
135
Output of the generalized technique in terms of
parameters of boundary defining parabolas
136
Output of the generalized technique in terms of
the current error space phasor boundary for
different operating frequencies
conventional Y-axis and X-axis 1div.0.5 A
137
Voltage vector selection in Sector-1 for forward
as well as reverse direction of rotation of
machine
Present vector ON Conditions to be satisfied and next vector to be switched ON Conditions to be satisfied and next vector to be switched ON Conditions to be satisfied and next vector to be switched ON Conditions to be satisfied and next vector to be switched ON Conditions to be satisfied and next vector to be switched ON Conditions to be satisfied and next vector to be switched ON
Present vector ON (y2-4p1 (x-h1)) ? 0 (y2-4p1 (x-h1)) ? 0 up to 24 Hz operation (x2-4(p2 (y-k2))) ? 0 25 Hz onwards operation (x2-4(p2 (y-k2))) ? 0 (y2-4(p3 (x-h3))) ? 0 (y2-4(p3 (x-h3))) ? 0 up to 24 Hz operation (x2-4(p4(y-k4))) ? 0 25 Hz onwards operation (x2-4(p4(y-k4))) ? 0
Present vector ON ijC ? 0 ijA ? 0 ijA ? 0 ijB ? 0 ijC?0 ijA?0 ijC ? 0 ijA ? 0 ijC ? 0 ijB ? 0 ijC ? 0 ijA ? 0
V1 - - - V2 - V7
V2 V1 - - - - V8
V7 - V1 V1 - V2 -
V8 - V1 V2 - V2 -
138
Sector changed detection using outer parabolic
boundary
Y-axis 1div.0.2 A and X-axis 1div.0.5 A
139
Sector change detection logic (based on outer
parabolic bands) for forward rotation of machine
From sector Present vector ON Condition to be satisfied for the sector change and next sector to be considered as new sector Condition to be satisfied for the sector change and next sector to be considered as new sector Condition to be satisfied for the sector change and next sector to be considered as new sector Condition to be satisfied for the sector change and next sector to be considered as new sector Condition to be satisfied for the sector change and next sector to be considered as new sector Condition to be satisfied for the sector change and next sector to be considered as new sector
From sector Present vector ON (y2-4(p3_outer(x-h3_outer))) ? 0 (y2-4(p3_outer(x-h3_outer))) ? 0 (y2-4(p3_outer(x-h3_outer))) ? 0 (y2-4(p1_outer(y-h1_outer))) ? 0 (y2-4(p1_outer(y-h1_outer))) ? 0 (y2-4(p1_outer(y-h1_outer))) ? 0
From sector Present vector ON ijA lt 0 ijB lt 0 ijB lt 0 ijC lt 0 ijC lt 0 ijA lt 0 ijC ? 0 ijA ? 0 ijA ? 0 ijB ? 0 ijB ? 0 ijC ? 0
1 V2 or V7 or V8 2
2 V3 or V7 or V8 3
3 V4 or V7 or V8 4
4 V5 or V7 or V8 5
5 V6 or V7 or V8 6
6 V1 or V7 or V8 1
( means continue with the same sector)
140
Simulation results of proposed hysteresis
controller
10 Hz Operation
141
Simulation results of proposed hysteresis
controller
10 Hz Operation
142
Simulation results of proposed hysteresis
controller
20 Hz Operation
143
Simulation results of proposed hysteresis
controller
20 Hz Operation
144
Simulation results of proposed hysteresis
controller
30 Hz Operation
145
Simulation results of proposed hysteresis
controller
30 Hz Operation
146
Simulation results of proposed hysteresis
controller
35 Hz Operation
147
Simulation results of proposed hysteresis
controller
35 Hz Operation
148
Simulation results of proposed hysteresis
controller
40 Hz Operation
149
Comparison of boundary obtained by theoretical
calculations and simulation studies for VC-SVPWM
based two-level VSI fed IM drive
SVPWM Simulation
10 Hz
30 Hz
35 Hz
40 Hz
Proposed Hysteresis Controller Simulation
150
Simulation results of proposed hysteresis
controller
47 Hz Operation
151
Simulation results of proposed hysteresis
controller
Six-Step Mode of Operation
152
Block schematic of experimental set-up used for
proposed hysteresis controller
153
Experimental results of proposed hysteresis
controller
vAN, 130 V/div.
?i, 0.2 A/div.
iA, 1.3 A/div.
10 Hz Operation
?i, Sector-2
?i, Sector-3
?i, Sector-1
154
Experimental results of proposed hysteresis
controller
iA, 1.3 A/div.
iA, 1.3 A/div.
i, 1 A/div.
10 Hz Operation
155
Experimental results of proposed hysteresis
controller
vAN, 130 V/div.
iA, 1.3 A/div.
?i, 0.35 A/div.
20 Hz Operation
?i, Sector-1
?i, Sector-2
?i, Sector-3
156
Experimental results of proposed hysteresis
controller
iA, 1.3 A/div.
iA, 1.3 A/div.
i, 1 A/div.
20 Hz Operation
iA, 1.3 A/div.
iA, 1.3 A/div.
157
Experimental results of proposed hysteresis
controller
vAN, 135 V/div.
iA, 1.3 A/div.
?i, 0.45 A/div.
30 Hz Operation
?i, Sector-3
?i, Sector-2
?i, Sector-1
158
Experimental results of proposed hysteresis
controller
iA, 1.3 A/div.
iA, 1.3 A/div.
?i, Sector-3, 0.45 A/div.
30 Hz Operation
iA, 1.3 A/div.
iA, 1.3 A/div.
i, 1 A/div.
159
Experimental results of proposed hysteresis
controller
vAN, 130 V/div.
iA, 1.3 A/div.
?i, 0.55 A/div.
35 Hz Operation
?i, Sector-2, 0.55 A/div.
?i, Sector-3-4, 0.55 A/div.
?i, Sector-3, 0.55 A/div.
160
Experimental results of proposed hysteresis
controller
iA, 1.3 A/div.
iA, 1.3 A/div.
iA, 1.3 A/div.
iA, 1.3 A/div.
35 Hz Operation
161
Experimental results of proposed hysteresis
controller
vAN, 130 V/div.
?i, 0.6 A/div.
iA, 1.3 A/div.
40 Hz Operation
?i, Sector-2, 0.6 A/div.
?i, Sector-3, 0.6 A/div.
?i, Sector-1, 0.6 A/div.
162
Experimental results of proposed hysteresis
controller
iA, 1.3 A/div.
?i, Sector-4-5, 0.6 A/div.
iA, 1.3 A/div.
40 Hz Operation
iA, 1.3 A/div.
iA, 1.3 A/div.
163
Experimental results of proposed hysteresis
controller
vAN, 130 V/div.
iA, 1.3 A/div.
?i, 0.6 A/div.
45 Hz Operation
164
Experimental results of proposed hysteresis
controller
vAN, 130 V/div.
?i, 0.5 A/div.
iA, 1.3 A/div.
47 Hz Operation
165
Experimental results of proposed hysteresis
controller
vAN, 130 V/div.
50 Hz Operation (Six-Step Mode)
iA, 1.3 A/div.
i, 1.4 A/div.
?i, 0.65 A/div.
166
Experimental results of proposed hysteresis
controller
vAN, 130 V/div.
Acceleration Transients
iA, 1.3 A/div.
167
Experimental results of proposed hysteresis
controller
speed, 910 rpm//div.
Starting Operation
iA, 1.3 A/div.
vAN, 160 V/div.
iA, 1.5 A/div.
iA, 1.5 A/div.
iA, 1.7 A/div.
168
Experimental results of proposed hysteresis
controller
speed, 910 rpm//div.
Starting Operation
iA, 1.3 A/div.
iA, 1.5 A/div.
vAN, 160 V/div.
iA, 1.5 A/div.
iA, 1.7 A/div.
169
Experimental results of proposed hysteresis
controller
speed, 910 rpm//div.
Speed Reversal
iA, 1.1 A/div.
iA, 1.35 A/div.
vAN, 130 V/div.
iA, 1.5 A/div.
iA, 1.35 A/div.
170
Experimental results of proposed hysteresis
controller
speed, 910 rpm//div.
Speed Reversal
iA, 1.1 A/div.
iA, 1.5 A/div.
vAN, 130 V/div.
iA, 1.65 A/div.
iA, 1.5 A/div.
171
Salient features of the proposed hysteresis
controller

• Current error space phasor based simple
  hysteresis controller
• Controls the switching frequency variation in a
  two-level VSI fed IM drive
• Based on the novel concept of on-line variation
  of hysteresis band, depending upon the speed of
  the machine
• Uses parabolic boundary for the current error
  space phasor
• Obtains switching frequency spectrum in the
  output voltage similar to that of the constant
  switching frequency VC-SVPWM based VSI fed IM
  drive.

172
Salient features of the proposed hysteresis
controller (Contd)

• Performance of the proposed controller is
  independent of the load machine parameters
• The unique parabolic boundary for different
  operating speeds for any given induction motor is
  determined using generalized technique (Matlab
  program) developed in proposed work
• Calculation of machine back emf vector is not
  needed
• Sector change logic is self-adaptive and is
  capable of taking the drive up to six-step mode
  of operation, if needed
• Controller always selects the adjacent inverter
  voltage vectors, forming a sector, in which the
  tip of the machine voltage vector lies

173
Multimotor drive setup
174
Multimotor drive setup
175
(No Transcript)
176
Inverter setup for multilevel structure
177
Inverter setup for multilevel structure
178
(No Transcript)
179
(No Transcript)
180
(No Transcript)
181
(No Transcript)