Lecture - PowerPoint PPT Presentation
Title:
Lecture
Description:
Peephole optimization ... to write a peephole optimizer that removes useless ... Peep Hole optimizations. Push r13 push it as an arg to - Movi 1 r14 r14 := 1 ... – PowerPoint PPT presentation
Number of Views:42
Avg rating:3.0/5.0
Title: Lecture
1
Lecture 9, May 3, 2007
- Project 2
- Peephole optimizations
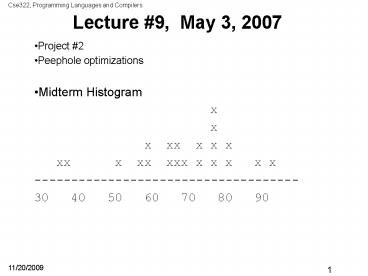
- Midterm Histogram
- x
- x
- x xx x x x
- xx x xx xxx x x x x x
- ------------------------------------
- 30 40 50 60 70 80 90
2
Assignments
- Project 1 is due today.
- Email me your solution by Midnight tonight
- All I want is your Phase1.sml file.
- PLEASE put your name as a comment in the file.
- Project 2 is officially assigned Tuesday May 8.
- Due 2 weeks from then, Tuesday May 22
- The template will be made available on Tuesday
- We will talk about it today in class
- Reading
- Optimizations
- Chapter 8 Section 8.4
- Chapter 10 Sections 10.1 10.3
3
Project 2
- Project 2 has three parts
- Putting IR code in canonical form
- See lecture 8 (More about IR1)
- Finalization of offsets
- Writing a simple peephole optimizer for IR1
- Project 2 is Due on Tuesday, May 22, 2007
- The template contains a complete solution to
Project 1, so you might not want it until you
hand in Project 1. - You may start Project 2 by using only the IR1.sml
file - The template provides a mechanism for testing
your code by parsing, and generating IR code for
you to transform. It is not necessary to have the
template to get started.
4
Canonical form
- Using the starting point discussed in Lecture 8
you should write a function that takes a IR.FUNC
list to a IR.FUNC list - It should remove all ESEQ constructors.
- The only expressions left should be pure ones
without any embedded statements. - This is a straightforward walk over all the IR
datatypes, as illustrated in lecture 8. - Just complete the code in S08code.sml from
the notes webpage
5
Finalizing offsets
- Recall, method parameters (PARAM), local method
variables (VAR), and object instance variables
(MEMBER) are all logical indexes. - The integer is the nth parameter, variables, or
instance. - We need to translate all these to a physical
offset - This requires computing the size of all
parameters, variables, and instances variables
and assigning an offset to each one. - Assumptions
- All variables have the same size (4 bytes)
- Information about variables can be computed from
information in the FUNC datastructure. True only
about parameters and local vars.
Not always the case for instance variables
6
Peephole optimization
- After canonicalization we often generate code
that could be simplified by looking at a small
window of IR statements. - For example useless jumps
- L0 if MEM(V1) 1 GOTO L1 Entry
x - JUMP L4
- L4 if MEM(V2) 1 GOTO L5 Entry
y (!z) - JUMP L2
- L5 if MEM(P1) 1 GOTO L2 Entry
!z - JUMP L1
- L1 T0 1 True
x (y (!z)) - JUMP L3
- L2 T0 0 False
x (y (!z)) - L3 Exit
x (y (!z)) - You are to write a peephole optimizer that
removes useless jumps at the minimum. You may add
other optimizations. - Extra credit for each additional optimization.
- To get credit you must
- Explain each optimization
- and provide tests that illustrate it
7
More about Initialization and offsets of instance
vars
- Finalizing offsets of instance variables is
tricky - class R int x 0 int y 1
- class S extends R int x2 int z 3
- class T extends S int y 4 int w 5
- x has offset 0
- y has offset 1
- z has offset 2
- w has offset 3
- But in S, x appears to have offset 0, and z
appears to have offset 1. - Initialization is also tricky
- R x 0 y 1
- S x2 y1 z 3
- T x2 y 4 z 3 w 5
8
Where is this information?
- We need to decide how to maintain and use this
information. - By the time the ProgramTypes code has been
translated to IR1, this information is sometimes
missing. - We need to do 2 things
- We need to construct a table, indexed by class
and instance variable name. - Make sure both class name and instance variable
name are available - We need both the instance variable and the class
name to access this information - obj.x Member(loc,obj,R,x)
- obj.x 25 Assign(SOME obj,x,NONE,25)
- obj.xi 25 Assign(SOME obj,x,SOME i,25)
Note class name is missing from assignments
9
Class Table
- class R int x 0 int y 1
- class S extends R int x2 int z 3
- class T extends S int y 4 int w 5
- datatype entry
- entry of string
- (string
- int
- Exp option) list
- type table entry list
- We must build this from
- ProgramTypes before translating,
- and use it in the finalization
- of offsets phase. It is also
- useful in the translation to
- IR1 phase (for the new object)
class variable offset initialization
10
The Class table
- datatype entry
- entry of string
- (int
- Type
- string
- Exp option) list
- type table entry list
- val classTable ref ( entry list)
Global reference variable, is set by the type
checker.
11
Class Table
- class R int x 0 int y 1
- class S extends R int x2 int z 3
- class T extends S int y 4 int w 5
- datatype entry
- entry of string
- (int string
- int
- Exp option) list
- type table entry list
class variable offset initialization
12
Fixing things
- class R int x 0 int y 1
- class S extends R int x2 int z 3
- super
sub - fix int x 0 int y 1 with int x2 int z
3 - int x 2 int y 1 int z 3
- The position in the super class is kept, but the
initialization of the sub class is kept. - Algorithm. For each var in super, scan over sub
looking for variable. If its there, replace the
initialization in super, and remove it from sub. - After all supers are scanned, add any subs left
to super.
13
ML code
- datatype entry entry of string
(stringintExp) list - type table entry list
- fun scan vSuper (NONE,)
- scan vSuper ((vSub,init)xs)
- if vSuper vSub
- then (SOME init,xs)
- else let val (exp,xs2) scan vSuper xs
- in (exp,(vSub,init)xs2) end
- fun number n
- number n ((v,exp)xs) (v,n,exp)number
(n1) xs - fun fix n sub number n sub
- fix n ((s,exp)ss) sub
- case scan s sub of
- (NONE,xs) gt (s,n,exp) fix (n1) ss xs
- (SOME init,xs) gt (s,n,init) fix (n1)
ss xs
scan over sub looking for variable. If its there,
replace the initialization in super, and remove
it from sub.
14
Does the order matter?
- Note we must process the super of the super (if
any) before we process the subclass, or it wont
have its position correct. - Solution.
- Perform an toplological sort
- Use the class table (CTab) returned by the type
checker to get the order correctly.
15
This code is in the template
- fun cName (ClassDec(loc,this,super,vars,methods))
this - fun cVars (ClassDec(loc,this,super,vars,methods))
vars - fun findInstVars name
- findInstVars name (ccs)
- if cName c name
- then let fun project(VarDecl(l,t,n,i))
(n,i) - in map project (cVars c) end
- else findInstVars name cs
- fun process n "object" sub classes
- entry(sub,fix 0 (findInstVars sub
classes)) - process n super sub classes
- entry(sub,fix n (findInstVars super classes)
- (findInstVars sub classes))
16
Small Changes to Program Types
- Old
- datatype Stmt
- Assign of Exp option Id Exp option Exp
- New
- datatype Stmt
- Assign of (Expstring) option Id
- (ExpBasic) option Exp
- This information is placed there by the type
checker.
17
Example use obj.x 99
- class T
- int instance2 0
- public int f(int j) return j
- class test05
- int instance1 0
- public int test(int param1, T object1)
- int var1 0
- object1.instance2 99
18
Translating
- fun pass1E env exp
- case exp of
- Assign(SOME (obj,class),x,NONE,v) gt
- ( non-array e.x v )
- let val target pass1E env obj
- val addr AddressOfMember env target
class x - val value pass1E env v
- in MOVE(addr,value) end
- MEM(P2) 1 99
Adds the offset of x in class to the address
target
19
Notes about Project 2
- The class Table
- I have installed a class table that is
initialized by the type checker. - All the pertinent information about classes and
instance variables is stored in the table. - The drivers
- The drivers give you means to run the parser, the
type checker, and the ir1 translation mechanism, - You may either return the data structures or
print them out. - templates for the three transformations
- I have provided a template for the three
transformations.
20
Example information
- class T has vars
- 0 int instance2 0
- class S has vars
- 0 int instance2 1
- 1 int y 5
- class R has vars
- 0 int instance2 0
- 1 int y 6
- 2 int w 10
- class test05 has vars
- 0 int i0 0
- 1 int i1 1
class T int instance2 0 class S extends
T int instance2 1 int y 5 class R
extends T int y 6 int w 10 class
test05 int i0 0 int i1 1
21
Access to the information
- You may access the information by fetching the
table from the reference variable - (! TypeChecker.classTable )
- Or you may print it out using
- TypeChecker. showTable ()
22
Template Drivers
- In the Driver file are a number of drivers you
can use to access the parser, the typechecker,
and the IR-translator. - fun parseFileToList file parse file true
- fun parseAndTypeCheck file
- TCProgram(parse file true)
- fun parseTypeCheckPass1 file
- case parseAndTypeCheck file of
- (classes,env) gt pass1P (Program classes)
23
Showing
- fun showParsedProgram file
- case parseFileToList file of
- Program cs gt print(plistf showClassDec ""
cs) - fun showTypeCheckedProgram file
- case parseAndTypeCheck file of
- (classes,env) gt print(plistf showClassDec
"" classes) - fun showPhase1IR file
- case parseAndTypeCheck file of
- (classes,env) gt
- let val cs pass1P (Program classes)
- val _ print "
" - val _ TypeChecker.showTable()
- val _ print "
\n" - in print(plistf IR1.sFUNC "\n" cs) end
24
Templates for the three transformations.
- structure Phase2 struct
- fun cannonical x x
- fun finalizeOffset table x x
- fun peephole x x
25
Writing the transformations.
- The work of the transformations is done on the
Exp and Stmt level. But the transformations work
over programs. - We need to drill our way down to the parts that
matter.
26
Cannonical
- fun cannonical (Program cs)
- map cannonicalC cs
- fun CannonicalC (ClassDec(loc,name,super,vs,ms))
- ClassDec(loc,name,super
- ,map cannonicalVs vs
- ,map cannonicalMs ms)
- fun CannonicalMs (MetDecl(loc,typ,nam,ps,vs,stmts)
) . . .
27
Finalize
- Finalize has a similar structure, but also takes
a class table as input. - This needs to be piped down as well.
- This will be useful when finalizing offsets for
member access and assignment.
28
What to turn in
- I will provide a template containing a parser,
pretty printer, and a type checker, just as
before, with the small changes I mentioned. - You will need to add the code for building and
passing around the class table. - Use your own IR translator, and add
- a post processing canonical phase
- A finalization of offsets
- A simple peephole optimizer
- Hand in just this one file.
29
Optimization
- We will look at a number of optimizations to low
level code. - Peephole
- Local Optimizations
- Constant Folding
- Constant Propagation
- Copy Propagation
- Reduction in Strength
- In Lining
- Common sub-expression elimination
- Loop Optimizations
- Loop Invariant s
- Reduction in strength due to induction variables
- Loop unrolling
- Global Optimizations
- Dead Code elimination
- Code motion
- Reordering
- code hoisting
30
Inefficiences
- Note that automatic translation schemes leaves
much to be desired. Consider - Push r13 push it as an arg to -
- Movi 1 r14 r14 1
- Push r14 push it as an arg to -
- Pop r15 get args to -
- Pop r16
- Prim - r15 r16 r10 r10 x2 -1
- In a stack machine, we push arguments on the
stack to protect them from recursive calls, only
to pop them without any recursive calls most of
the time.
31
Another Example
- Pop r9 pop the result of recursive call
- Push r9 push it as arg to
- Pop r17 pop the two args to times
- Pop r18
- Prim r17 r18 r6 perform the multiply
- Here we pop things, only to immediately push them
back on the stack.
32
Peep Hole optimizations
- Push r13 push it as an arg to -
- Movi 1 r14 r14 1
- Push r14 push it as an arg to -
- Pop r15 get args to -
- Pop r16
- Prim - r15 r16 r10 r10 x2 -1
- In the first example r14 is never mentioned
anywhere but in those two instructions. So we
could remove the Push Pop sequence by renaming
r15 by r14 everywhere . - Push r13 push it as an arg to -
- Movi 1 r14 r14 1
- Pop r16
- Prim - r14 r16 r10 r10 x2 -1
33
Code Movement
- Push r13 push it as an arg to -
- Movi 1 r14 r14 1
- Pop r16
- Prim - r14 r16 r10 r10 x2 -1
- Now note that the Movi instruction doesn't change
the stack, so we could move it before the Push
(or after the Pop) getting - Movi 1 r14 r14 1
- Push r13 push it as an arg to -
- Pop r16
- Prim - r14 r16 r10 r10 x2 -1
- But now we have a Push Pop sequence!
- Movi 1 r14 r14 1
- Prim - r14 r13 r10 r10 x2 -1
34
Peephole Pattern Matching Implementation
- Using pattern matching, this is easy to
implement. - First we need a function that in a code sequence
substitutes one register for another everywhere. - Next we need to express the patterns we are
looking for. - Finally we need to apply these patterns on every
code sequence. - What does a pattern look like?
- (Push x) (Pop y) moreInstrs
35
Subreg
- fun subreg M instr
- let fun lookup x x
- lookup ((y,v)m) x
- if xy then v else lookup m x
- in case instr of
- Init gt Init
- Halt gt Halt
- Movi(n,r) gt Movi(n,lookup M r)
- Mov(r1,r2) gt
- Mov(lookup M r1, lookup M r2)
- Inc(r,n) gt Inc(lookup M r,n)
- Push r gt Push (lookup M r)
- Pop r gt Pop(lookup M r)
- Ld(r1,r2) gt
- Ld(lookup M r1, lookup M r2)
36
Subreg (continued)
- St(r1,r2) gt
- St(lookup M r1, lookup M r2)
- Sw(r1,r2) gt
- Sw(lookup M r1, lookup M r2)
- Brz(r,n) gt Brz(lookup M r,n)
- Brnz(r,n) gt Brnz(lookup M r,n)
- Skip n gt Skip n
- Prim(s,rs,r) gt
- Prim(s,map (lookup M) rs,lookup M r)
- Label s gt Label s
- Movl(s,r) gt Movl(s,lookup M r)
- Goto s gt Goto s
- Brzl(r,s) gt Brzl(lookup M r,s)
- Brnzl(r,s) gt Brnzl(lookup M r,s)
- end
37
peep function
- fun peep ans reverse ans
- peep ((Push r1)(Pop r2)m) ans
- peep (map (subreg (r2,r1)) m) ans
- peep ((i as (Push r1))
- (z as ((Movi(n,r2))
- (Pop r3) m))) ans
- if r1ltgtr2
- then peep
- (map (subreg (r3,r1)) m)
- ((Movi(n,r2))ans)
- else peep z (ians)
- peep (iis) ans peep is (ians)
38
How does this work?
Think of it as a pair of instruction streams
where we move instructions from one stream to
the other. Push r13 push it as an arg to
- Movi 1 r14 r14 1 Push r14 push it
as an arg to - Pop r15 get args to - Pop
r16 Prim - r15 r16 r10 r10 x2 -1
Prim 15,16 10
Push 13
Movi 1 14
Push 14
Pop15
Pop 16
input
X
Y
ans
39
Example
- fun peep ans reverse ans
- peep ((Push r1)(Pop r2)m) ans
- peep (map (subreg (r2,r1)) m) ans
- peep ((i as (Push r1))
- (z as ((Movi(n,r2))
- (Pop r3) m))) ans
- if r1ltgtr2 then peep (map (subreg (r3,r1))
m) ((Movi(n,r2))ans) - else peep z (ians)
- peep (iis) ans peep is (ians)
Prim 15,16 10
Movi 1 14
Push 13
Push 14
Pop15
Pop 16
input
ans
X
Y
Prim 15,16 10
Pop 16
input
Push 14
Pop15
Movi 1 14
ans
Push 13
X
Y
40
Example (continued 1)
Prim 14,16 10
input
Pop 16
Movi 1 14
ans
Push 13
X
Y
input
Prim 14,16 10
Movi 1 14
ans
Pop 16
Push 13
X
Y
Start over again
Prim 14,16 10
Movi 1 14
input
Pop 16
Push 13
Y
X
ans
Prim 14,16 10
input
Movi 1 14
Pop 16
Push 13
ans
Y
X
41
Example (Continued 2)
Prim 14,16 10
input
Movi 1 14
Pop 16
Push 13
ans
Y
X
Prim 14,13 10
input
ans
Movi 1 14
Y
X
input
Prim 14,13 10
Movi 1 14
ans
Y
X
Prim 14,13 10
Movi 1 14
Y
X