96 Finite Math Lecture 4 Systems of equations

1
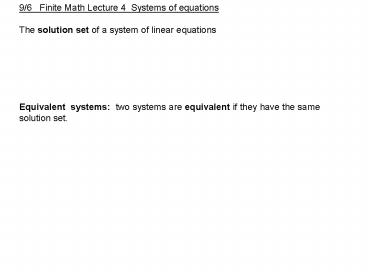
9/6 Finite Math Lecture 4 Systems of equations
The solution set of a system of linear
equations Equivalent systems two systems
are equivalent if they have the same solution
set.
2
An inconsistent system is one with 0 solutions
Example x y 2 2x
2y 3
3
A consistent system is one with 1 or more
solutions Example 1 x y 1
-x y 1 Example 2 x y 1
2x 2y 2
4
Row operations 1. Summing Add a multiple of one
row to another row 2. Scaling multiply a row
by a nonzero number 3. Swapping Interchange two
rows Use these operations to reduce a system
to row echelon form the top
equation has all variables, the 2nd equation
does not have the 1st variable, the 3rd
equation does not have the 1st or 2nd variables,
etc Once a system is in row echelon form, you
can easily say whether it is consistent, and, if
it is consistent, whether it 1 or many solutions.

5
Example 1 Common version 7u 3w -3x -3 3u
2w 2x 2 -u 6w 6x-2
6
The augmented matrix of a system is convenient
to work with. Example 1 x y z 3
x 2y z 1 y
z 2
7
Example 2 Common 6 Find k so that the
system
does not have a unique soln. -7s ky -1
3s - 7y -7
8
Traffic flow problems Given the capacities of
all the roads leading into and out of a town,
determine the needed capacities of the roads in
the town.

9