Grade Scale

1
Grade Scale

• Quiz 4 Results
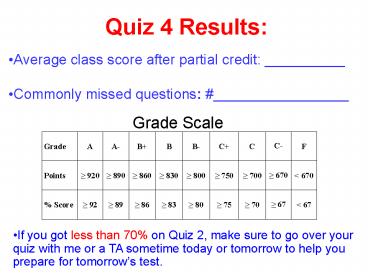
• Average class score after partial credit
  __________
• Commonly missed questions _________________

• If you got less than 70 on Quiz 2, make sure to
  go over your quiz with me or a TA sometime today
  or tomorrow to help you prepare for tomorrows
  test.

2
Big lesson from Quiz 4

• CHECK YOUR ANSWERS!!
• Factoring problems Multiply the factors back out
  and see if you get the original polynomial for
  your answer.
• Solve problems Plug the answers (numbers) back
  into the original equation and see if it comes
  out equal on both sides.

3
Review For Test 2
4
Test 2 CoversSection 4.1 (Systems of
linear equations in 2 variables)Chapter 5
(Properties of exponents, operations on
polynomials, factoring polynomials, solving
polynomial equations)Section 8.2 (Quadratic
formula)
5
To study for the test

• 1). Take Practice Test 2.
• 2). Review Quizzes 3 and 4 from the online
  Gradebook.
• 3). Review the homework from the sections in
  which you missed questions on the practice test.
  (Review homework by using the Gradebook
  function, not the Assignments button.)
• 4). Review your notes and the online lecture
  slides (under each Assignment).

6
Practice Test Tips

• Your best score on the practice test DOES count
  10 points toward your course grade. A 100 score
  gives you 10 points, 50 gives you 5 points, and
  not taking it at all gives you 0 out of the 15
  points.
• You can take the practice test as many times as
  you want, and only your best score will count for
  points.
• The practice test has the same number of
  questions (20) as the real test.
• Each time you take the practice test, you will
  get a different set of questions. The more times
  you take it, the more likely you will see all of
  the types of question that will be on the real
  test.
• When you REVIEW a completed practice test, you
  will be able to use the Help Me Solve This and
  other learning aids, but they will not be
  available as you take the practice test or the
  real test.
• Its also a good idea to come in and review a
  completed practice test with a teacher or tutor
  in the open lab before you take the regular test
  in class.

7
Math TLC Open Lab Hours

• Room 403 Harvey Hall
• Monday through Thursday
• 800 a.m. 730 p.m.

8
Another good study aidChapter Highlights
pages in bookCh. 4 page 247 (sec. 4.1 only)
Ch. 5 pages 330-332 (all) Ch. 8 page 533
(sec. 8.2 only)(You can find these in either
the on-line or the paper textbook.)
9
Section 4.1 Review

• Determine whether the given point is a solution
  of the following system.
• point (-3, 1)
• system x y -4 and 2x 10y 4
• Plug the values into the equations.
• First equation -3 1 -4 true
• Second equation 2(-3) 10(1) -6 10 4
  true
• Since the point (-3, 1) produces a true statement
  in both equations, it is a solution.

10

• Solve the following system of equations using the
  substitution method.
• y 2x 5 and 8x 4y 20
• Since the first equation is already solved for y,
  substitute this value into the second equation.
• 8x 4y 20
• 8x 4(2x 5) 20 (replace y with
  result from first equation)
• 8x 8x 20 20 (use distributive
  property)
• 20 20 (simplify left side)

11

• When you get a result, like the one on the
  previous slide, that is obviously true for any
  value of the replacements for the variables, this
  indicates that the two equations actually
  represent the same line.
• There are an infinite number of solutions for
  this system. Any solution of one equation would
  automatically be a solution of the other
  equation.
• The answer is written as (x,y) y 2x 5

12

• Solve the following system of equations using the
  elimination method.
• 6x 3y -3 and 4x 5y -9
• Multiply both sides of the first equation by 5
  and the second equation by 3.
• First equation,
• 5(6x 3y) 5(-3)
• 30x 15y -15 (use the distributive
  property)
• Second equation,
• 3(4x 5y) 3(-9)
• 12x 15y -27 (use the distributive
  property)

13

• Combine the two resulting equations (eliminating
  the variable y).
• 30x 15y -15
• 12x 15y -27
• 42x -42
• x -1 (divide both sides by 42)

14

• Substitute the value for x into one of the
  original equations.
• 6x 3y -3
• 6(-1) 3y -3 (replace the x value in
  the first equation)
• -6 3y -3 (simplify the left
  side)
• -3y -3 6 3 (add 6 to
  both sides and simplify)
• y -1 (divide both sides by -3)
• Our computations have produced the point (-1,-1).

15

• Check the point in the original equations.
• First equation,
• 6x 3y -3
• 6(-1) 3(-1) -3 true
• Second equation,
• 4x 5y -9
• 4(-1) 5(-1) -9 true
• The solution of the system is (-1, -1).

16

• Solve the following system of equations using the
  elimination method.

• First multiply both sides of the equations by a
  number that will clear the fractions out of the
  equations.

17

• Multiply both sides of each equation by 12.
  (Note you dont have to multiply each equation
  by the same number, but in this case it will be
  convenient to do so.)
• First equation,

18
Second equation,

• Combine the two equations.
• 8x 3y -18
• 6x 3y -24
• 14x -42
• x -3 (divide both
  sides by 14)

19

• Substitute the value for x (-3) into one of the
  equations to determine the value for y.
• 8x 3y -18
• 8(-3) 3y -18
• -24 3y -18
• 3y -18 24 6
• y 2
• Our computations have produced the point (-3, 2).

20

• Check the point in the original equations.
  (Note Here you should use the original
  equations before any modifications, even though
  they involve fractions, to detect any
  computational errors that you might have made.)

First equation,
Second equation,

• The solution is the point (-3, 2).

21

• Use of the addition method to combine two
  equations might lead you to results like . . .
• 5 5 (which is always true, thus indicating that
  there are infinitely many solutions, since the
  two equations represent the same line), or
• 0 6 (which is never true, thus indicating that
  there are no solutions, since the two equations
  represent parallel lines).
• Remember, if there are infinitely many solutions,
  the solution set is (x,y) (write in one of
  the two equations)

22
Section 5.1/5.2 review

• Summary of Exponent Rules

Product Rule for exponents am an amn
Power Rule for exponents (am)n amn
Power of a Product (ab)n an bn
Zero exponent a0 1, a ? 0
23
Simplify each of the following expressions.
Compare to the result of 2323 233 26 64
(23)3
29
512
233
(x4)2
x8
x42
Compare to the result of x4x2 x42 x6
24
Simplify by writing the following expression with
positive exponents or calculating.
(3-2- -4 a3-7 b1- - 3)-2 (32 a -4 b 4)-2
32-2 a-4-2 b4-2 3-4 a8 b-8 a 8
34b8 a8 81b8
25
Scientific Notation
Write each of the following in scientific
notation.
Since we moved the decimal 3 places, and the
original number was gt 10, our count is positive 3.
4700 4.7 ? 103
Since we moved the decimal 4 places, and the
original number was lt 1, our count is negative 4.
0.00047 4.7 ? 10-4
26

• Multiplying and dividing with numbers written in
  scientific notation involves using properties of
  exponents.

Perform the following operations.
(7.3 8.1) ? (10-2 105)
59.13 ? 103
5.913 x 104
(sci. notation)
59,130 (standard form)
3 x 10 -6
(sci. not.)
(standard form)
27

• Review on your own
• (should be fairly fresh in your
  memory!)
• Section 5.3 adding/subtracting polynomials
• Section 5.4 multiplying polynomials
• Sections 5.5-5.7 factoring polynomials
• Section 5.8 solving polynomial equations by
  factoring.
• Section 8.2 solving second degree polynomial
  equations using the quadratic formula.

28
Reminders

• Be on time so youre logged in and ready to go
  when I give you the password.
• (This is especially important for tests since
  they will take the entire 55-minute class
  period.)
• Bring your POWER CORD.
• REMEMBER TO SHOW ALL OF YOUR WORK on the
  answer/worksheet provided so that we can award
  partial credit for partially correct work or
  typos.

29

• Do any of you who have already started the
  practice test have any questions youd like to
  have explained?

30

• If theres time left, go ahead and start the
  practice test, and well come around to help if
  you have questions.
• Remember, come to the open lab next door if you
  want help going over anything on your practice
  test.

31
Math TLC Open Lab Hours

• Room 403 Harvey Hall
• Monday through Thursday
• 800 a.m. 730 p.m.