Forward chaining: an overview

1
Forward chaining an overview

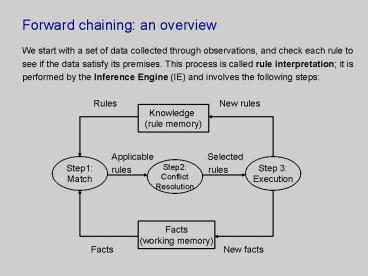
• We start with a set of data collected through
  observations, and check each rule to
• see if the data satisfy its premises. This
  process is called rule interpretation it is
• performed by the Inference Engine (IE) and
  involves the following steps
• Rules
  New rules
• Applicable
  Selected
• rules
  rules
• Facts
  New facts

Knowledge (rule memory)
Step1 Match
Step 3 Execution
Step2 Conflict Resolution
Facts (working memory)
2
The fruit identification example (adapted from
Dankel Gonzalez)

• Consider a KBS intended to recognize different
  fruits provided fruit descriptions.
• Assume that the set of rules consists of the
  following rules.
• Rule 1 If (shape long) and (color green)
  
• Then (fruit banana)
• Rule 1A If (shape long) and (color yellow)
  
• Then (fruit banana)
• Rule 2 If (shape round) and (diameter gt 4
  inches)
• Then (fruitclass vine)
• Rule 2A If (shape oblong) and (diameter gt 4
  inches)
• Then (fruitclass vine)
• Rule 3 If (shape round) and (diameter lt 4
  inches)
• Then (fruitclass tree)
• Rule 4 If (seedcount 1)
• Then (seedclass stonefruit)
• Rule 5 If (seedcount gt 1)
• Then (seedclass multiple)
• Rule 6 If (fruitclass vine) and (color
  green)
• Then (fruit watermelon)

3
The fruit identification example (cont.)

• Rule 7 If (fruitclass vine) and (surface
  smooth) and (color yellow)
• Then (fruit honeydew)
• Rule 8 If (fruitclass vine) and (surface
  rough) and (color tan)
• Then (fruit cantaloupe)
• Rule 9 If (fruitclass tree) and (color
  orange) and (seedclass stonefruit)
• Then (fruit apricot)
• Rule 10 If (fruitclass tree) and (color
  orange) and (seedclass multiple)
• Then (fruit orange)
• Rule 11 If (fruitclass tree) and (color
  red) and (seedclass stonefruit)
• Then (fruit cherry)
• Rule 12 If (fruitclass tree) and (color
  orange) and (seedclass stonefruit)
• Then (fruit peach)
• Rule 13 If (fruitclass tree) and (color
  red) and (seedclass multiple)
• Then (fruit apple)
• Rule 13A If (fruitclass tree) and (color
  yellow) and (seedclass multiple)
• Then (fruit apple)
• Rule 13B If (fruitclass tree) and (color
  green) and (seedclass multiple)
• Then (fruit apple)

4
The fruit identification example (cont.)

• Assume the following set of facts comprising the
  initial working memory
• FB ((diameter 1 inch) (shape round)
  (seedcount 1)
• (color red))
• The forward reasoning process is carried out as
  follows
• Cycle 1
• Step1 (matching) Rules 3 and 4 are applicable
• Step2 (conflict resolution) Select rule 3
• Step 3 (execution) FB ? (fruitclass tree)
• Cycle 2
• Step1 (matching) Rules 3 and 4 are applicable
• Step2 (conflict resolution) Select rule 4
• Step 3 (execution) FB ? (seedclass stonefruit)

5
The fruit identification example (cont.)

• Cycle 3
• Step1 (matching) Rules 3, 4 and 11 are
  applicable
• Step2 (conflict resolution) Select rule 11
• Step 3 (execution) FB ? (fruit cherry)
• Cycle 4
• Step1 (matching) Rules 3, 4 and 11 are
  applicable
• Step2 (conflict resolution) No new rule can be
  selected. Stop.
• Note, that there are many variations of the
  described forward-chaining strategy.
• The TRE system from our textbook, for example,
  fires all applicable rules not
• a selected rule. This way, it makes sure that all
  possible conclusions are
• inferred, rather than selected ones.

6
Forward chaining general rule format

• Rules used to represent diagnostic or
  procedural knowledge have the following
• format
• If ltantecedent 1gt is true,
• ltantecedent 2gt is true,
• ltantecedent igt is true
• Then ltconsequentgt is true.
• The rule interpretation procedure utilizes
  unification (or renaming), which states
• that one sentence is a renaming of another if
  they are the same except for the
• names of pattern variables.
• Examples
• likes(x, ice-cream) is a renaming of likes(y,
  ice-cream)
• flies(bird1) is a renaming of flies(bird2), and
  both are renamings of flies(Tom).
• Here x, y, bird1 and bird2 are pattern variables.

7
Pattern matching

• To recognize pattern variables more easily, we
  will arrange them in two-element
• lists, where the first element is ?, and the
  second element is the pattern variable.
• Examples
• (color (? X) red)
• (color apple (? Y))
• (color (? X) (? Y))
• If the pattern contains no pattern variables,
  then the pattern matches the basic
• statement (called a datum) iff the pattern and
  the datum are exactly the same.
• Example Pattern (color apple red) matches datum
  (color apple red).
• If the pattern contains a pattern variable, then
  an appropriate substitution must be
• found to make the pattern match the datum.
• Example Pattern (color (? X) red) matches datum
  (color apple red) given substitution ? x /
  apple

8
Pattern matching (cont.)

• To implement pattern matching, we need a
  function, match, which works as
• follows
• gt (match (color (? X) red) (color apple
  red))
• ((X apple))
• gt (match ((? Animal) is a parent of (?
  Child)) (Tim is a parent of Bob))
• ((Child Bob) (Animal Tim))
• (? _) will denote anonymous variables these
  match everything.
• Example (color (? _) (? _)) match (color apple
  red), (color grass green), etc.

9
Object streams

• Streams are lists of objects intended to be
  processed in the exact order in
• which they appear in the stream, namely from the
  front to the back of the
• stream. When a new object is added to the stream,
  it must be added to its back.
• To represent streams, we can use ordinary lists.
  Then, first allow us to access
• the first element, and rest will trim the first
  element off. However, we can also
• access the other elements of the list by means of
  second, third, etc., thus
• violating the definition of the stream. To
  prevent this from happening, streams
• will be represented as two-element lists, where
  the first element is the first
• object in the stream, and the second element is
  itself a stream.
• Example
• 'empty-stream
• EMPTY-STREAM
• (stream-cons 'object1 'empty-stream)
• (OBJECT1 EMPTY-STREAM)
• (stream-cons 'object1 '(OBJECT1 EMPTY-STREAM) )
• (OBJECT1 (OBJECT1 EMPTY-STREAM))

10
Operations on streams

• (defun stream-endp (stream) (eq stream
  'empty-stream))
• (defun stream-first (stream) (first stream))
• (defun stream-rest (stream) (second stream))
• (defun stream-cons (object stream) (list object
  stream))
• (defun stream-append (stream1 stream2)
• (if (stream-endp stream1) stream2
• (stream-cons (stream-first stream1)
• (stream-append
  (stream-rest stream1)
• 
  stream2))))
• (defun stream-concatenate (streams)
• (if (stream-endp streams) 'empty-stream
• (if (stream-endp (stream-first streams))
• (stream-concatenate (stream-rest
  streams))
• (stream-cons (stream-first
  (stream-first streams))
• (stream-concatenate
• (stream-cons
  (stream-rest
• 
  (stream-first streams)) (stream-rest
  streams)))))))

11
Operations on streams (cont.)

• (defun stream-transform (procedure stream)
• (if (stream-endp stream) 'empty-stream
• (stream-cons (funcall procedure
  (stream-first stream))
• (stream-transform
  procedure
• 
  (stream-rest stream)))))
• (defun stream-member (object stream)
• (cond ((stream-endp stream) nil)
• ((equal object (stream-first
  stream)) t)
• (t (stream-member object
  (stream-rest stream)))))
• (defmacro stream-remember (object variable)
• (unless (stream-member ,object ,variable)
• (setf ,variable
• (stream-append ,variable
• (stream-cons ,object
  'empty-stream)))
• ,object))
• Here STREAM-REMEMBER is a macro that inserts new
  assertions at the end of the stream, so that

12
An implementation of forward chaining

• The Zoo example considered here is adopted from
  Winston Horn. The KBS
• is intended to identify animals provided their
  descriptions. Assume that all facts
• about the domain are stored in the fact base,
  assertions, represented as a
• stream, and all rules are stored in the rule
  base, rules, also represented as a
• stream. Pattern variables make it possible for a
  rule to match the fact base in a
• different way. Let us keep all such possibilities
  in a binding stream.
• Example Consider the following rule set
  containing just one rule
• ((identify
• ((? Animal) is a (? Species))
• ((? Animal) is a parent of (? Child))
• ((? Child) is a (? Species)))
  empty-stream)
• Let the fact base contains the following
  facts
• ((Bozo is a dog) ((Deedee is a horse)
  ((Deedee is a parent of sugar)
• ((Deedee is a parent of Brassy)
  empty-stream))))

13
Example (cont.)

• The first match produces the following
  two-element binding stream
• (((species dog) (animal bozo))
• ((species horse) (animal deedee))
  empty-stream)
• Next, the second rule antecedent is matched
  against each of the assertions in the
• fact base. However, this time we have the binding
  list from the first step, which
• suggests particular substitutions
• Matching ((? Animal) is a parent of (? Child))
  against the fact base fails for substitution
  ((species dog) (animal bozo))
• Matching ((? Animal) is a parent of (? Child))
  against the fact base given the substitution
  ((species horse) (animal deedee)) succeeds
  resulting in a new binding list
• (((child sugar) (species horse)
  (animal deedee))
• ((child brassy) (species horse)
  (animal deedee)) empty-stream)

14
Backward chaining

• Assume the same representation of rules as in
  forward chaining, i.e.
• If ltantecedent 1gt is true,
• ltantecedent 2gt is true,
• ltantecedent igt is true
• Then ltconsequentgt is true.
• Rule interpretation starts with (i) an empty fact
  base, and (ii) a list of goals which
• the system tries to derive, and consists of the
  following steps
• Form a stack initially composed of all
  top-level goals.
• Consider the first goal from the stack, and
  gather all of the rules capable of satisfying
  this goal.
• For each of these rules, examine the rules
  premises
• If all premises are satisfied, execute the rule
  to infer its conclusion, and remove the satisfied
  goal from the stack.

15
Backward chaining (cont.)

• ii. If there is a premise which is not
  satisfied, look for rules by means of which this
  premise can be derived if such rules exist, add
  the premise as a sub-goal on the top of the
  stack, and go to 2.
• iii. If no rule exists to satisfy the unknown
  premise, place a query to the user and add the
  supplied value to the fact base. If the premise
  cannot be satisfied, consider the next rule which
  has the initial goal as its conclusion.
• If all rules that can satisfy the current goal
  have been attempted, and all failed, then the
  goal is unsatisfiable remove the unsatisfiable
  goal from the stack and go to 2. If the stack is
  empty (i.e. all of the goals have been satisfied)
  stop.

16
The fruit identification example

• Assuming that we do not have any information
  about the object that we are
• trying to recognize, let the top-level goal be
  (fruit (? X)).
• Step1 Initial fact base ( )
• Initial stack of goals ((fruit (?
  X)))
• Step 2 Rules capable of satisfying this goal
  are 1, 6, 7, 8, 9, 10, 11, 12, 13, 14.
• Step 3 Consider Rule 1. Its first premise is
  (shape long). There is no data in the FB
  matching this premise and no rule has (shape (?
  Y)) as its conclusion. Therefore, a query is
  placed to the user to acquire for the shape of
  the fruit under consideration. Assume that the
  user replies that the fruit is round, i.e. the
  current FB becomes
• Current fact base ((shape round)).
• Rule 1 fails, and Rule 6 is examined next.
  The first premise of Rule 6 results in a new goal
  which is added at the beginning of the current
  stack of goals.
• Current stack of goals ((fruitclass (? Y))
  (fruit (? X)))

17
The fruit identification example (cont.)

• There are two rules capable of satisfying
  the newly stated goal, namely Rule 2 and Rule 3.
  The first premise of Rule 2, (shape round),
  matches a datum in the FB. The second premise
  leads to a new query regarding the diameter of
  the fruit. Assume that the answer is (diameter
  1 inch).
• Current fact base ((shape round)(diameter
  1 inch)).
• Rule 2 fails, and Rule 3 is examined next.
  It succeeds, thus a new conclusion, (fruitclass
  tree) is added to the FB and the first goal is
  removed from the current stack of goals.
• Current fact base ((shape round)(diameter
  1 inch)(fruitclass tree)).
• Now Rules 6, 7 and 8 fail, and Rule 9 is
  examined next. Its first premise succeeds, but
  its second premise places a new query regarding
  the color of the fruit. Assume that the user
  enters (color red), which fails Rules 9 and 10.
  The first two premises of Rule 11 are satisfied,
  the third premise places a query regarding the
  seedclass. Assume that the user enters (seedclass
  stonefruit), resulting in Rule 11 being
  satisfied, and its conclusion (fruit cherry)
  added to the FB. Note that this proves our
  top-level goal.
• Current fact base ((shape
  round)(diameter 1 inch)(fruitclass
  tree)(color red)(seedclass stonefruit)(fruit
  cherry)).
• Current stack of goals ()
• Step 4 Stop, no more goals remain to be proved.

18
Types of Pattern-Directed Inference Systems

• All PDISs use assertions to represent declarative
  knowledge, and rules to
• represent procedural knowledge. However, they can
  defer in the way they
• search for a solution. Our textbook suggests the
  following classification of PDIS
• Forward-chaining PDIS.
• Backward-chaining PDIS.
• PDIS using production rules, where the search
  strategy selects a single best rule to fire,
  rather than all applicable rules.
• Procedural deduction systems. These use
  pattern-matching, but their procedural knowledge
  lacks the modularity typical for rule-based PDIS.
• We shall primarily discuss forward-chaining PDISs
  assuming that a PDIS is a
• part of a larger system, which starts up the PDIS
  and makes use of its output.