EART 160: Planetary Science

1
EART 160 Planetary Science
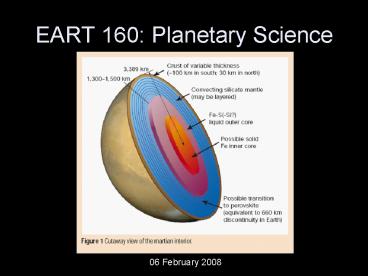
06 February 2008
2
Last Time

• Planetary Surfaces
• Summary
• Planetary Interiors
• Terrestrial Planets and Icy Satellites
• Structure and Composition What all is inside?
• Exploration Geophysics How can we tell?

3
Today

• Homework 3 graded
• Projects Have you got a topic yet?
• Midterm Friday! details
• Paper Discussion Stevenson (2001)
• Mars Magnetic Field
• Planetary Interiors
• Pressure and Temperature
• Heat Sources and Cooling Mechanisms
• Rheology

4
Mean 35 St. Dev. 8
5
Homework Issues

• Please talk to me if you have difficulties
• Before class is not usually a good time
• No more Monday due dates
• Units
• Pressure 1 Pa 1N m-2 1 kg m-1 s-2
• Energy 1 J 1 kg m2 s-2
• Power 1 W 1 J s-1
• Stress
• Tectonic stress is not the Lithostatic Pressure
• Normal stress is the Pressure normal component
  of Tectonic
• Shear stress is the tangential component of
  Tectonic

6
Midterm Exam

• Closed-book
• I will provide a formula sheet
• You may provide an 8.5 11 sheet of paper with
  whatever you want on it hand it in with your
  test.
• Formulae wont help you if you dont understand
  them!
• Several short-answer questions, descriptive
• 3 quantitative problems, pick 2 to answer
• Similar to Homework, but less involved
• Show your work!
• Review Session? What say ye?

7
Exam Topics

• Orbital Mechanics
• Keplers Laws, Newtons Laws
• Conservation of Energy, Momentum, Angular
  Momentum
• Escape Velocity
• Solar System Formation
• Composition of the Solar Nebula
• Jeans Collapse
• Accretion and Runaway Growth
• Frost Line
• Meteorites and Asteroids
• Chondrites Remnants from Early Solar System
• Role of collisions
• Radiometric Dating

8
Impacts

• Crater size depends on impactor size, impact
  velocity, surface gravity
• Crater morphology changes with increasing size
• Simple vs. complex crater vs. impact basin
• Depthdiameter ratio
• Crater size-frequency distribution can be used to
  date planetary surfaces
• Energetics, Global effects due to impacts
• Atmospheres and geological processes can affect
  size-frequency distributions

9
Volcanism

• Solidus liquidus
• Magmatism when solidus crosses adiabat
• Higher temperatures, reduced pressure or lowered
  solidus
• Volcanism when buoyant magma erupts
• Conductive cooling time t d2/k
• Magma composition controls style of volcanism
• Flow controlled by viscosity
• Viscous materials s h de/dt

10
Tectonics

• Planetary cooling leads to compression
• Hookes law and Youngs modulus
• Elastic materials s E e
• Contraction and cooling
• Byerlees law
• Styles of tectonicsm compression, extension,
  shear

11
Gradation

• Erosion on planets with atmospheres
• Aeolian, Fluvial, Glacial
• Mass Wasting, Sputtering everywhere.
• Valley networks, gullies and outflow channels

12
Planets are like Ogres

• Compositional Layers
• Core Metal
• Mantle Dense silicate rock (peridotite)
• Crust thin silicate rock (basalt)
• Ocean liquid layer
• Atmosphere gas layer

• Mechanical Layers
• Inner Core solid metal
• Outer Core liquid metal
• Lower Mantle High viscosity silicate
• Aesthenosphere ductile upper mantle
• Lithosphere Brittle uppermost mantle and crust

ON an icy satellite, the ocean will be beneath
the icy mantle. Other ice phases are denser than
water. May have ice ocean -- ice
13
Actual Planetary Interiors
Venus
Io
Earth
Mars
Mercury
Ganymede
Moon
Only Earth has an layered core The Moon has a
TINY core (why?) Icy satellites may have liquid
oceans beneath the ice shell High-Pressure Ices
beneath that.
Interior of Europa -- NASA
14
Stevenson et al., 2001 Nature
15
Pressures inside planets

• Hydrostatic assumption (planet has no strength)

• For a planet of constant density r (is this
  reasonable?)

• So the central pressure of a planet increases as
  the square of its radius
• Moon R1800km, P7.2 GPa
• Mars R3400km, P26 GPa

16
Pressures inside planets

• The pressure inside a planet controls how
  materials behave
• E.g. porosity gets removed by material compacting
  and flowing, at pressures few MPa
• The pressure required to cause a materials
  density to change significantly depends on the
  bulk modulus of that material

The bulk modulus K controls the change in density
(or volume) due to a change in pressure

• Typical bulk modulus for silicates is 100 GPa
• Pressure near base of mantle on Earth is 100 GPa
• So change in density from surface to base of
  mantle should be roughly a factor of 2 (ignoring
  phase changes)

17
Real planets

• Notice the increase in mantle density with depth
  is it a smooth curve?
• How does gravity vary within the planet?

18
Phase Transitions

• Under pressure, minerals transform to different
  crystal structure
• How do we detect this?
• Transition zone can sore a LOT of water!
• How do the depths change on other planets?

19
Temperature

• Planets generally start out hot (see below)
• But their surfaces (in the absence of an
  atmosphere) tend to cool very rapidly
• So a temperature gradient exists between the
  planets interior and surface
• We can get some information on this gradient by
  measuring the elastic thickness, Te
• The temperature gradient means that the planet
  will tend to cool down with time

20
Heat Sources

• Accretion and Differentiation
• U Eacc
• Eacc m Cp DT
• Cp specific heat
• Radioactive Decay
• E H m
• H 5x10-12 W kg-1
• K, U, Th today
• Al, Fe early on
• Tidal Heating in some satellites

21
Specific Heat Capacity Cp

• The specific heat capacity Cp tells us how much
  energy needs to be added/subtracted to 1 kg of
  material to make its temperature
  increase/decrease by 1K
• Energy mass x specific heat capacity x temp.
  change
• Units J kg-1 K-1
• Typical values rock 1200 J kg-1 K-1 , ice 4200 J
  kg-1 K-1
• E.g. if the temperature gradient near the Earths
  surface is 25 K/km, how fast is the Earth cooling
  down on average? (about 170 K/Gyr)
• Why is this estimate a bit too large?
• Atmosphere insulates

22
Energy of Accretion

• Lets assume that a planet is built up like an
  onion, one shell at a time. How much energy is
  involved in putting the planet together?

In which situation is more energy delivered?
early
later
If accretion occurs by lots of small impacts, a
lot of the energy may be lost to space If
accretion occurs by a few big impacts, all the
energy will be deposited in the planets
interior So the rate and style of accretion (big
vs. small impacts) is important, as well as how
big the planet ends up
Total accretional energy
If all this energy goes into heat, what is the
resulting temperature change?
Is this a reasonable assumption?
Earth M6x1024 kg R6400km so DT30,000K Mars
M6x1023 kg R3400km so DT6,000K What do we
conclude from this exercise?
23
Cooling a planet

• Large silicate planets (Earth, Venus) probably
  started out molten magma ocean
• Magma ocean may have been helped by thick early
  atmosphere (high surface temperatures)

• Once atmosphere dissipated, surface will have
  cooled rapidly and formed a solid crust over
  molten interior
• If solid crust floats (e.g. plagioclase on the
  Moon) then it will insulate the interior, which
  will cool slowly ( Myrs)
• If the crust sinks, then cooling is rapid (
  kyrs)
• What happens once the magma ocean has solidified?

24
Cooling

• Radiation
• Photon carries energy out into space
• Works if opacity is low
• Unimportant in interior, only works at surface
• Conduction
• Heat transferred through matter
• Heat moves from hot to cold
• Slow dominates in lithosphere and boundary
  layers
• Convection
• Hot, buoyant material carried upward, Cold, dense
  material sinks
• Fast! Limited by viscosity of material

Running down the stairs with buckets of ice is
an effective way of getting heat upstairs. --
Juri Toomre
25
Conduction - Fouriers Law
T1gtT0
T0

• Heat flow F

d
F
T1

• Heat flows from hot to cold (thermodynamics) and
  is proportional to the temperature gradient
• Here k is the thermal conductivity (W m-1 K-1)
  and units of F are W m-2 (heat flux is power per
  unit area)
• Typical values for k are 2-4 Wm-1K-1 (rock, ice)
  and 30-60 Wm-1K-1 (metal)
• Solar heat flux at 1 A.U. is 1300 W m-2
• Mean subsurface heat flux on Earth is 80 mW m-2
• What controls the surface temperature of most
  planetary bodies?

26
Diffusion Equation

• We can use Fouriers law and the definition of Cp
  to find how temperature changes with time

F2
dz
F1

• Here k is the thermal diffusivity (k/rCp) and
  has units of m2 s-1
• Typical values for rock/ice 10-6 m2s-1

In steady-state, the heat produced inside the
planet exactly balances the heat loss from
cooling. In this situation, the temperature is
constant with time
27
Diffusion length scale

• How long does it take a change in temperature to
  propagate a given distance?
• This is perhaps the single most important
  equation in the entire course
• Another way of deducing this equation is just by
  inspection of the diffusion equation
• Examples
• 1. How long does it take to boil an egg?
• d0.02m, k10-6 m2s-1 so t6 minutes
• 2. How long does it take for the molten Moon to
  cool?
• d1800 km, k10-6 m2s-1 so t100 Gyr.
• What might be wrong with this answer?

28
Internal Heating

• Assume we have internal heating H (in Wkg-1)
• From the definition of Cp we have HtDTCp
• So we need an extra term in the heat flow
  equation

• This is the one-dimensional, Cartesian thermal
  diffusion equation assuming no motion
• In steady state, the LHS is zero and then we just
  have heat production being balanced by heat
  conduction
• The general solution to this steady-state problem
  is

29
Example

• Lets take a spherical, conductive planet in
  steady state
• In spherical coordinates, the diffusion equation
  is

• The solution to this equation is

Here Ts is the surface temperature, R is the
planetary radius, r is the density

• So the central temperature is Ts(rHR2/6k)
• E.g. Earth R6400 km, r5500 kg m-3, k3 Wm-1K-1,
  H6x10-12 W kg-1 gives a central temp. of
  75,000K!
• What is wrong with this approach?

30
Convection

• Convective behaviour is governed by the Rayleigh
  number Ra
• Higher Ra means more vigorous convection, higher
  heat flux, thinner stagnant lid
• As the mantle cools, h increases, Ra decreases,
  rate of cooling decreases -gt self-regulating
  system

Stagnant lid (cold, rigid)
Plume (upwelling, hot)
Sinking blob (cold)
Image courtesy Walter Kiefer, Ra3.7x106, Mars
31
Viscosity

• Ra controls vigor of convection. Depends
  inversely on viscosity, h .
• Viscosity depends on Temperature T, Pressure P,
  Stress s, Grain Size d.

A pre-exponential constant E Activation
Energy V Activation Volume R Gas Constant n
Stress Exponent m Grain-size exponent
Viscosity relates stress and strain rate
32
Viscoelasticity

• A Maxwellian material has a viscous term and an
  elastic term.
• If h is high, we get an elastic behavior. If h
  is low, we get a viscous behavior.
• Depends also on the rate of stress. Materials
  are elastic on a short timescale, viscous on a
  long one.
• There are other types of viscoelasticity, but
  Maxwell is the simplest

m
33
Elastic Flexure

• The near-surface, cold parts of a planet (the
  lithosphere) behaves elastically
• This lithosphere can support loads (e.g.
  volcanoes)
• We can use observations of how the lithosphere
  deforms under these loads to assess how thick it
  is
• The thickness of the lithosphere tells us about
  how rapidly temperature increases with depth i.e.
  it helps us to deduce the thermal structure of
  the planet
• The deformation of the elastic lithosphere under
  loads is called flexure
• EART163 Planetary Surfaces

34
Flexural Stresses
load
Crust
Elastic plate
Mantle

• In general, a load will be supported by a
  combination of elastic stresses and buoyancy
  forces (due to the different density of crust and
  mantle)
• The elastic stresses will be both compressional
  and extensional (see diagram)
• Note that in this example the elastic portion
  includes both crust and mantle

35
Flexural Parameter
load
rw

• Consider a load acting on an elastic plate

Te
a
rm

• The plate has a particular elastic thickness Te
• If the load is narrow, then the width of
  deformation is controlled by the properties of
  the plate
• The width of deformation a is called the flexural
  parameter and is given by

E is Youngs modulus, g is gravity and n is
Poissons ratio (0.3)
36

• If the applied load is much wider than a, then
  the load cannot be supported elastically and must
  be supported by buoyancy (isostasy)
• If the applied load is much narrower than a, then
  the width of deformation is given by a
• If we can measure a flexural wavelength, that
  allows us to infer a and thus Te directly.
• Inferring Te (elastic thickness) is useful
  because Te is controlled by a planets
  temperature structure

a
37
Example
10 km

• This is an example of a profile across a rift on
  Ganymede
• An eyeball estimate of a would be about 10 km
• For ice, we take E10 GPa, Dr900 kg m-3 (there
  is no overlying ocean), g1.3 ms-2

Distance, km

• If a10 km then Te1.5 km
• A numerical solution gives Te1.4 km pretty
  good!
• So we can determine Te remotely
• This is useful because Te is ultimately
  controlled by the temperature structure of the
  subsurface

38
Te and temperature structure

• Cold materials behave elastically
• Warm materials flow in a viscous fashion
• This means there is a characteristic temperature
  (roughly 70 of the melting temperature) which
  defines the base of the elastic layer

• E.g. for ice the base of the elastic layer is at
  about 190 K
• The measured elastic layer thickness is 1.4 km
  (from previous slide)
• So the thermal gradient is 60 K/km
• This tells us that the (conductive) ice shell
  thickness is 2.7 km (!)

110 K
270 K
190 K
1.4 km
Depth
elastic
viscous
Temperature
39
Te in the solar system

• Remote sensing observations give us Te
• Te depends on the composition of the material
  (e.g. ice, rock) and the temperature structure
• If we can measure Te, we can determine the
  temperature structure (or heat flux)
• Typical (approx.) values for solar system objects

40
Next Time

• Paper Discussion Stevenson (2001)
• Planetary Interiors
• Cooling Mechanisms
• Rheology How does the material deform?
• Magnetism