per fun

1
periodic functions
2
General Graphs

• Graphs are collections of points
• Independent variables are related to dependent
  variables
• Domain is set of independent variable values
• Range is set of dependent variable values

3
Modeling real world behavior

• Why do we learn about functions?

• Do you remember what kind of function we used to
  model each situation?

Linear
Time (in hrs) 0.5 1 1.5 2
Distance (miles) 30 60 90 120
4
Modeling real world behavior
Path of baseball

• Do you remember what kind of function we used to
  model each situation?

Quadratic
Ground zero
5
Modeling real world behavior

• Do you remember what kind of function
• we used to model this situation?

6
HERES THE POINT

• How do we graph these?
• What function could we use to mimic these?

7
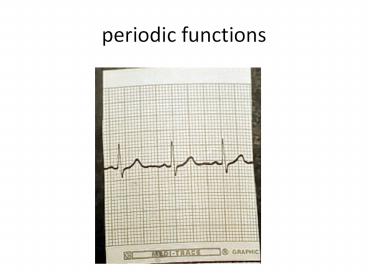
High Tide and Low Tide
8

• Definitions
• Periodic function repeats a pattern of y
  values(outputs) at regular intervals.
• Cycle one complete pattern
• The period (or wavelength) is the length of one
  complete cycle.

9

• Definitions
• The midline is the horizontal line midway between
  the minimum and maximum values.
• The amplitude is the distance between the maximum
  (or minimum) and the midline.

10
Cycle One complete pattern of the function. A
cycle can occur at any point on the graph of the
function Period the horizontal length of one
cycle of the function. Midline is the
horizontal line midway between the minimum and
maximum values. Amplitude is the distance
between the maximum (or minimum) and the
midline, or half distance between max and min.
Amplitude
Cycle
midline
Period
Period
11
Exploring Periodic Data
Analyze this periodic function. Identify one
cycle in two different ways. Then determine the
period of the function.
The period of the function is 7.
The midline is y 0
The amplitude is 2
Each cycle is 7 units long.
12
Exploring Periodic Data
Determine whether each function is or is not
periodic. If it is, find the period.
The pattern of y-values in one section repeats
exactly in other sections. The function is
periodic.
Find points at the beginning and end of one cycle.
Subtract the x-values of the points 2 0 2.
The pattern of the graph repeats every 2 units,
so the period is 2.
The midline is y 0
The amplitude is 2
13
Exploring Periodic Data
(continued)
b.
The pattern of y-values in one section repeats
exactly in other sections. The function is
periodic.
Find points at the beginning and end of one cycle.
Subtract the x-values of the points 3 0 3.
The pattern of the graph repeats every 3 units,
so the period is 3.
The midline is y 3
The amplitude is 3
14
Periodic Graphs

• The most common periodic graphs are the graphs of
  the trigonometric functions
• Sine, cosine, and tangent

15
We are interested in the graph of y sin x
Start with a "t" chart and let's choose values
from our unit circle and find the sine values for
various angles on the unit circle.
plot these points
? y sin ?
16
y f(x) sin x
choose more values
? y sin ?
plot these points
join the points
If we continue picking values for x we will start
to repeat since this is periodic.
17
The Sine Graph
1
1
Cycle one complete pattern of the graph
Period- time (horizontal distance) it takes the
graph to complete one cycle
Amplitude-the furthest vertical distance the
graph goes from the midline
18
The parent function Sine Graphf(x) sin(x)
1
1

• The period of the sine graph is

• Since your calculator thinks of x and units of
  one, approximately where will the sine graph
  finish one cycle?

6.28

• The amplitude of the sine graph is(maximum
  vertical distance from the center)

1
19
The Cosine Parent functionf(x) cos(x)
1
1

• Same period

• Same amplitude

• The starting point is still an x-value of zero,
  but is now a y-value of 1 because the cos(0) is 1
• The big difference between sin and cos graph is
  that cos starts at (0, -1) and sin(x) starts at
  (0,0),

20
Graph sin and cos in graphing calculator

• Make sure calculator is set to radians
• Go to y and enter cos(x)
• Push Zoom and then Ztrig
• Repeat with sin(x)

21
The Cosine Graph

• The cosine graph is the same as the sine graph,
  only it has been shifted horizontally
• Graph Y2 cos(x) and press graph

• Notice, Same period and same amplitude

22
Sine and Cosine Graphs

• While the idea of a starting point is very
  helpful when graphing, it is merely an idea,
  there is no beginning or ending
• These graphs have infinite domains