Complex Variables

1
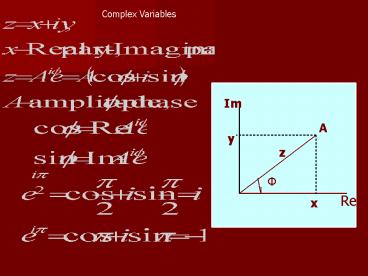
Complex Variables
Im
A
y
z
F
Re
x
2
(No Transcript)
3
(No Transcript)
4
Hyperbolic Functions
The hyperbolic trigonometric functions are
defined as
We know that ex grows as x increases and decays
as x decreases, while e-x decays as x increases
and grows as x decreases.
5
Putting this all together we get the following
curve for sinh(x)
6
Here's the curve for the cosh(x) function
7
(No Transcript)
8

• The free oscillation of any real physical system
  always die away with passage of time.
• Every real system has dissipation of its energy
  due action of dissipative or resistive forces on
  it.
• What is the form of dissipative force or
  resistive force?

• Resistive force is proportional to velocity but
  exerted in opposite direction to the velocity.
• Fresistive -bv,
• where b is positive constant called damping
  constant

9
Let us consider mass-spring system with resistive
force
ma
-bv
-kx
10
So equation of motion will be
11
To solve it, we try a solution of the form
Where C and a are constants C
has dimension of length and a has
dimension of inverse of time
Substituting the derivatives in the equation
12
So either
(Which is trivial)
13
Or
Solving for a gives
b/2m vk/m both have dimension of inverse time
14

• Bracket (b2/4m2-k/m) can be positive, zero or
  negative
• Each value of this bracket describes particular
  type of behaviour

15
Case 1. b2/4m2 gt k/m or bracket term is ve
or Fresistive gt Frestoring
Motion is Heavily Damped
Take b/2m p (b2/4m2-k/m)1/2 q
where C1 and C2 are arbitrary constants
Let us take F and G as F C1C2 and
G C1C2
16
The displacement is given by
This represents non-oscillatory behaviour Actual
displacement depends upon the initial conditions
i.e. the value of x at t0
17
If x0 at t0 then F0, and x (t) is given by
It will return to zero displacement quite slowly
without oscillating about its equilibrium position
18
(No Transcript)
19
Animations for SHM

• Damped SHM

20
Case 2. Critical Damping (b2/4m2 k/m
) Using same notation , we see that q0 and
xCe-at This is the limiting case of behaviour of
Case 1 as q changes from ve to ve value
Let q is very small (nearly equal to zero)
where A is constant length and B is given
velocity
21
Practical importance of critical damping in
BALLISTIC GALVANOMETER
It experiences sudden impulses and is required to
return to zero displacement in the minimum time
Let x0 at t0 and it receives electric charge
which gives initial velocity V over a linear scale
22
The return to zero in critically damped system is
reached in minimum time
23
Case 3. Damped Simple Harmonic Motion
b2/4m2 lt k/m i. e. Frestoring gt Fresistive
(b2/4m2 k/m)1/2 is an imaginary quantity
24
(No Transcript)
25
(No Transcript)
26
(No Transcript)
27
Therefore displacement varies sinusoidally with
time but with new frequency ?.
28
The presence of term bv introduces a loss of
energy which causes amplitude to decay with
time as
29
Damped SHM

• The solution of damped equation is

30
(No Transcript)
31
Damped Oscillations

• Critical damping
• - System no longer oscillates but simply relaxes
  to the equilibrium position.
• Overdamping
• - Damping increased beyond critically damped,
  system returns to equilibrium position with
  greater time

32
critically damped
overdamped
underdamped
33
Animations for SHM

• Circular Motion
• Spring Mass system
• Damped SHM
• Driven SHM