Point Symmetry

1
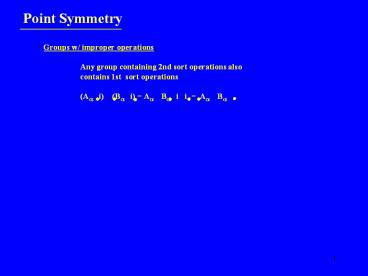
Point Symmetry
Groups w/ improper operations Any group
containing 2nd sort operations also contains 1st
sort operations (Aa i) (Ba i) Aa
Ba i i Aa Ba
2
Point Symmetry
Groups w/ improper operations Any group
containing 2nd sort operations also contains 1st
sort operations (Aa i) (Ba i) Aa
Ba i i Aa Ba 1st sort operations
in such a group G form a subgroup of index
2 g 1 a2 .
an Bg B Ba2 .
Ban B is any 2nd sort operation in G
3
Point Symmetry
Groups w/ improper operations Any group
containing 2nd sort operations also contains 1st
sort operations (Aa i) (Ba i) Aa
Ba i i Aa Ba 1st sort operations
in such a group G form a subgroup of index
2 g 1 a2 .
an Bg B Ba2 .
Ban B is any 2nd sort operation in G (Ba
i) ar (Ba ar) i all 2nd sort operations
in Bg
1st sort
4
Point Symmetry
Groups w/ improper operations 1. Any group of
2nd sort contains equal nos. of operations of
1st 2nd sort 2. In any group of the 2nd sort,
1st sort operations form a subgroup of index
2
5
Point Symmetry
Groups w/ improper operations 1. Any group of
2nd sort contains equal nos. of operations of
1st 2nd sort 2. In any group of the 2nd sort,
1st sort operations form a subgroup of index
2 3. A group of the 2nd sort can be formed by
adding any second sort operation (and its
products) to a group such that it transforms
that group into itself
6
Point Symmetry
Groups w/ improper operations 1. Any group of
2nd sort contains equal nos. of operations of
1st 2nd sort 2. In any group of the 2nd sort,
1st sort operations form a subgroup of index
2 3. A group of the 2nd sort can be formed by
adding any second sort operation (and its
products) to a group such that it transforms
that group into itself 4. All groups of the 2nd
sort can be formed by starting with all groups
of the 1st sort adding each possible 2nd sort
operation (i or m) products which transforms
the group into itself
7
Point Symmetry
Groups w/ improper operations Any rotoinversion
axis, except those for which n 4N, can be
decomposed into a combination of rotation axis
inversion or reflection
8
Point Symmetry
Groups not containing i G g, ng g, gn
(g of index 2cosets n transforms g into
itself) For every pt grp G of 1st sort which
can be expressed as product of subgroup g of
index 2 and operation of 1st sort n (n even),
can get a corresponding group G from same
subgrp 2nd sort operation n
9
Point Symmetry
Groups not containing i G g, ng g, gn
(g of index 2cosets n transforms g into
itself) For every pt grp G of 1st sort which
can be expressed as product of subgroup g of
index 2 and operation of 1st sort n (n even),
can get a corresponding group G from same
subgrp 2nd sort operation n 2 (m) 4
6 (If n odd, order of n 2x that of
n)
10
Point Symmetry
11
Point Symmetry

• C4 C4 C4
• C2 C2 C4 C2 C4 C2 C4

2
3
3
2

• C4 C4 C4
• m m C4 m C4 m C4

2
3
3
2
12
Point Symmetry
Groups containing i wrt i, any proper point
group is of index 2 i transforms any group
into itself So, get new groups by G i
13
Point Symmetry
G G i 1 1 2 2/m 3 3 4 4/m
6 6/m 222 2/m 2/m 2/m 32 3 2/m 422 4/m
2/m 2/m 622 6/m 2/m 2/m 23 2/m 3 432 4/m
3 2/m
14
Point Symmetry

• 4 i 4/m
• C4 C2 C4
• i i C4 i C2 i C4

G G i 1 1 2 2/m 3 3 4 4/m
6 6/m 222 2/m 2/m 2/m 32 3 2/m 422 4/m
2/m 2/m 622 6/m 2/m 2/m 23 2/m 3 432 4/m
3 2/m
-1
-1
15
Point Symmetry

• 4 i 4/m
• C4 C2 C4
• i i C4 i C2 i C4
• 2 i 2/m
• C2
• i i C2

G G i 1 1 2 2/m 3 3 4 4/m
6 6/m 222 2/m 2/m 2/m 32 3 2/m 422 4/m
2/m 2/m 622 6/m 2/m 2/m 23 2/m 3 432 4/m
3 2/m
-1
-1
16
Point Symmetry

• 4 i 4/m
• C4 C2 C4
• i i C4 i C2 i C4
• 2 i 2/m
• C2
• i i C2
• 2' i 2'/m'

G G i 1 1 2 2/m 3 3 4 4/m
6 6/m 222 2/m 2/m 2/m 32 3 2/m 422 4/m
2/m 2/m 622 6/m 2/m 2/m 23 2/m 3 432 4/m
3 2/m
-1
-1
l
l