Symmetry Operations

1
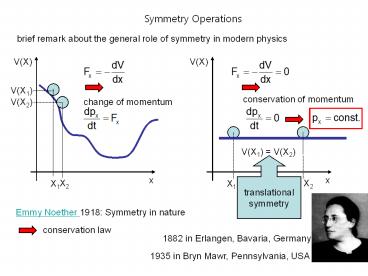
Symmetry Operations
brief remark about the general role of symmetry
in modern physics
conservation of momentum
change of momentum
V(X1) V(X2)
translational symmetry
Emmy Noether 1918 Symmetry in nature
conservation law
1882 in Erlangen, Bavaria, Germany
1935 in Bryn Mawr, Pennsylvania, USA
2
Example for symmetry in QM
angular momentum conserved J good quantum number
Hamiltonian invariant with respect to rotation
Zeeman splitting
Breaking the symmetry with magnetic field
Proton and Neutron 2 states of one particle
breaking the Isospin symmetry
Magnetic phase transition
3
Symmetry in perfect single crystals
ideally perfect single crystal
infinite
three-dimensional
repetition
of
identical building blocks
basis
very complex molecular structure
Volume of space (parallelepiped) fills all of
space by translation of discrete distances
Quantity of matter contained in the unit cell
4
Example crystal from
hexagonal unit cell
square unit cell
there is often more than one reasonable choice of
a repeat unit (or unit cell)
most obvious symmetry of crystalline solid
Translational symmetry
n21
3D crystalline solid
3 translational basis vectors a, b, c
n12
-by parallel extensions the basis vectors form a
parallelepiped, the unit cell, of volume Va(bxc)
translational operation
-connects positions with identical atomic
environments
5
concept of translational invariance is more
general
physical property at r (e.g.,electron density)
is also found at
rrT
Set of operations
Tn1an2bn3c
defines
r
space lattice
or
Bravais lattice
purely geometrical concept


6
lattice and translational vectors a, b,c are
primitive if every point r equivalent to r      
is created by
T
according to
rrT
Primitive basis
minimum number of atoms in the primitive
(smallest) unit cell which is sufficient to
characterize crystal structure
No integer!
7
2 important examples for primitive and non
primitive unit cells
face centered cubic
1atom/Vprimitive
4 atoms/Vconventinal
Primitive cell rhombohedron

body centered cubic
1atom/Vprimitive
2 atoms/Vconventinal
8
Lattice Symmetry
Symmetry of the basis
point group symmetry
has to be consistent with
symmetry of Bravais lattice
No change of the crystal after symmetry operation
(point group of the basis must be a point group
of the lattice)
Operations (in addition to translation) which
leave the crystal lattice invariant

• Reflection at a plane

9

• Rotation about an axis

H2o
2 -fold rotation axis
NH3
SF5 Cl
Cr(C6H6)2
Click for more animations and details about point
group theory
10

• point inversion

• Glide

reflection translation
rotation translation

• Screw

11
Notation for the symmetry operations

rotation by 2?/n degrees reflection through
plane perpendicular to rotation axis
Origin of the Symbols after Schönflies
Eidentity from the German Einheit unity
Cn Rotation (clockwise) through an angle 2p/n,
with n integer
? mirror plane from the German Spiegelmirror
?h horizontal mirror plane, perpendicular to
the axis of highest symmetry
?v vertical mirror plane, passing through the
axis with the highest symmetry
12
n-fold rotations with n1, 2, 3,4 and 6 are the
only rotation symmetries consistent with
translational symmetry
!
?
?
?
?
?
?
?
Intuitive example pentagon
13
Two-dimensional crystal with lattice constant a
in horizontal direction
1
a
2
(m-1)
Row A
Row B
m
1
If rotation by a is a symmetry operation
1
and
m
positions of atoms in row B
(m-1)a 2a
2a cos a
p-m
-1
1
0/2p
-2
1/2
p/3
-3
0
p/2
-4
-1/2
2p/3
-5
-1
p
14
Plane lattices and their symmetries
4mm
Point-group symmetry of lattice 2
2mm
2mm
6 mm
5 two-dimensional lattice types
Crystallatticebasis may have lower symmetry
10 types of point groups (1, 1m, 2, 2mm,3, 3mm,
4, 4mm, 6, 6mm)
possible basis
Combination of point groups and translational
symmetry
15
Three-dimensional crystal systems
Special relations between axes and angles
14 Bravais (or space) lattices
16
7 crystal systems
17
There are 32 point groups in 3D, each compatible
with one of the 7 classes
32 point groups and compound operations applied
to 14 Bravais lattices
230 space groups or structures exist