Working with relationships between two variables PowerPoint PPT Presentation
1 / 20
Title: Working with relationships between two variables
1
Correlation Regression
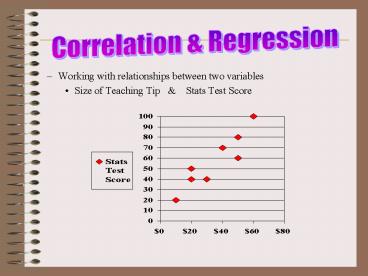
- Working with relationships between two variables
- Size of Teaching Tip Stats Test Score
2
Correlation Regression
- Univariate Bivariate Statistics
- U frequency distribution, mean, mode, range,
standard deviation - B correlation two variables
- Correlation
- linear pattern of relationship between one
variable (x) and another variable (y) an
association between two variables - relative position of one variable correlates with
relative distribution of another variable - graphical representation of the relationship
between two variables - Warning
- No proof of causality
- Cannot assume x causes y
3
Scatterplot!
- No Correlation
- Random or circular assortment of dots
- Positive Correlation
- ellipse leaning to right
- GPA and SAT
- Smoking and Lung Damage
- Negative Correlation
- ellipse learning to left
- Depression Self-esteem
- Studying test errors
4
Pearsons Correlation Coefficient
- r indicates
- strength of relationship (strong, weak, or none)
- direction of relationship
- positive (direct) variables move in same
direction - negative (inverse) variables move in opposite
directions - r ranges in value from 1.0 to 1.0
-1.0 0.0
1.0
Strong Negative No Rel.
Strong Positive
- Go to website!
- playing with scatterplots
5
Practice with Scatterplots
r .__ __
r .__ __
r .__ __
r .__ __
6
(No Transcript)
7
Correlation Guestimation
8
(No Transcript)
9
Samples vs. Populations
- Sample statistics estimate Population parameters
- M tries to estimate µ
- r tries to estimate ? (rho greek symbol ---
not p) - r correlation for a sample
- based on a the limited observations we have
- ? actual correlation in population
- the true correlation
- Beware Sampling Error!!
- even if ?0 (theres no actual correlation), you
might get r .08 or r -.26 just by chance. - We look at r, but we want to know about ?
10
Hypothesis testing with Correlations
- Two possibilities
- Ho ? 0 (no actual correlation The Null
Hypothesis) - Ha ? ? 0 (there is some correlation The
Alternative Hyp.) - Case 1 (see correlation worksheet)
- Correlation between distance and points r -.904
- Sample small (n6), but r is very large
- We guess ? lt 0 (we guess there is some
correlation in the pop.) - Case 2
- Correlation between aiming and points, r .628
- Sample small (n6), and r is only moderate in
size - We guess ? 0 (we guess there is NO correlation
in pop.) - Bottom-line
- We can only guess about ?
- We can be wrong in two ways
11
Reading Correlation Matrix
r -.904
p .013 -- Probability of getting a
correlation this size by sheer chance. Reject Ho
if p .05.
sample size
r (4) -.904, p?.05
12
Predictive Potential
- Coefficient of Determination
- r²
- Amount of variance accounted for in y by x
- Percentage increase in accuracy you gain by using
the regression line to make predictions - Without correlation, you can only guess the mean
of y - Used with regression
20
0
80
100
60
40
13
Limitations of Correlation
- linearity
- cant describe non-linear relationships
- e.g., relation between anxiety performance
- truncation of range
- underestimate stength of relationship if you
cant see full range of x value - no proof of causation
- third variable problem
- could be 3rd variable causing change in both
variables - directionality cant be sure which way
causality flows
14
Regression
- Regression Correlation Prediction
- predicting y based on x
- e.g., predicting.
- throwing points (y)
- based on distance from target (x)
- Regression equation
- formula that specifies a line
- y bx a
- plug in a x value (distance from target) and
predict y (points) - note
- y actual value of a score
- y predict value
- Go to website!
- Regression Playground
15
Regression Graphic Regression Line
See correlation regression worksheet
16
Regression Equation
- y bx a
- y predicted value of y
- b slope of the line
- x value of x that you plug-in
- a y-intercept (where line crosses y access)
- In this case.
- y -4.263(x) 125.401
- So if the distance is 20 feet
- y -4.263(20) 125.401
- y -85.26 125.401
- y 40.141
See correlation regression worksheet
17
SPSS Regression Set-up
- Criterion,
- y-axis variable,
- what youre trying to predict
- Predictor,
- x-axis variable,
- what youre basing the prediction on
Note Never refer to the IV or DV when doing
regression
18
Getting Regression Info from SPSS
See correlation regression worksheet
y b (x) a y -4.263(20)
125.401
a
19
Predictive Ability
- Mantra!!
- As variability decreases, prediction accuracy ___
- if we can account for variance, we can make
better predictions - As r increases
- r² increases
- variance accounted for increases
- the prediction accuracy increases
- prediction error decreases (distance between y
and y) - Sy decreases
- the standard error of the residual/predictor
- measures overall amount of prediction error
- We like big rs!!!
20
Drawing a Regression Line by Hand
- Three steps
- Plug zero in for x to get a y value, and then
plot this value - Note It will be the y-intercept
- Plug in a large value for x (just so it falls on
the right end of the graph), plug it in for x,
then plot the resulting point - Connect the two points with a straight line!