Sin t

1
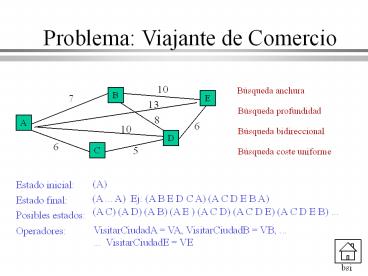
Problema Viajante de Comercio
Búsqueda anchura
Búsqueda profundidad
Búsqueda bidireccional
Búsqueda coste uniforme
(A)
Estado inicial
(A ... A) Ej (A B E D C A) (A C D E B A)
Estado final
(A C) (A D) (A B) (A E ) (A C D) (A C D E) (A C D
E B) ...
Posibles estados
VisitarCiudadA VA, VisitarCiudadB VB, ... ...
VisitarCiudadE VE
Operadores
bsi
2
Problema Viajante de Comercio
ÁRBOL DE BÚSQUEDA (ejemplo haciendo uso de costes)
(A)
VB
VE
7
VC
VD
10
6
13
(A B)
(A C)
(A E)
(A D)
VD
5
(A C D)
VE
6
(A C D E)
10
VB
(A C D E B)
7
VA
(A C D E B A)
3
Búsqueda en anchura
Expande primero los nodos menos profundos
(A)
(A B)
(A C)
(A E)
(A D)
.....................................
Completa?
Si, si b es finito
Si
Optima?
En el peor de los casos se expanden todos los
nodos hasta el nivel de la solución (d). O
(bd) (1b b2...bd ) En cada nivel se expanden
b nodos, por cada nodo de ese nivel
Complejidad espacial y temporal?
4
Búsqueda en profundidad
Expande primero los nodos no expandidos más
profundos
(A)
(A B)
(A C)
(A E)
(A D)
(A B D)
(A B E)
(A B A)
(A B E D)
(A B D C)
(A B D E)
(A B D A)
(A B E A)
(A B E D C)
(A B E D A)
(A B D C A)
(A B D E A)
(A B E D C A)
Completa?
No, falla en espacios de profundidad infinita
(puede haber bucles, estados repetidos)
No, puede encontrar un camino peor
Optima?
Complejidad temporal?
En el peor de los casos se expanden todos los
nodos hasta el nivel de máx profundidad (m). O
(bm)
Complejidad espacial?
Factor de ramificación profundidad de la
solución. O (bm) (lineal!)
5
Búsqueda bidireccional
Simultáneamente desde estado inicial hasta
objetivo y viceversa
(A)
(A C D E B A)
Completa?
Si
Se garantiza si se utiliza en ambos sentidos
búsqueda en anchura
Si
Optima?
Complejidad espacial y temporal?
En cada sentido O (bd/2) O (bd/2) O (bd/2) O
(bd/2) ltlt O (bd)
6
Búsqueda de coste uniforme
Expande primero los nodos no expandidos con menor
coste de camino
(A)
Completa?
Si
Si, si se cumple que g(suc(n)) gt g(n)
Optima?
Complejidad espacial y temporal?
Nº de nodos con g(n) lt coste de la solución
optima. O (bd)
Búsqueda primero en anchura es una búsqueda de
coste uniforme con g(n)profundidad(n)
7
Comparación de las estrategias de búsqueda ciega