MultiFingered Transistors - PowerPoint PPT Presentation
1 / 49
Title:
MultiFingered Transistors
Description:
Digital Integrated Circuits2nd. Combinational Circuits. Multi-Fingered Transistors. One finger ... At every point in time (except during the switching ... – PowerPoint PPT presentation
Number of Views:65
Avg rating:3.0/5.0
Title: MultiFingered Transistors
1
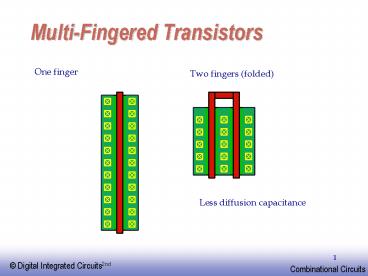
Multi-Fingered Transistors
One finger
Two fingers (folded)
Less diffusion capacitance
2
Digital Integrated CircuitsA Design Perspective
Jan M. Rabaey Anantha Chandrakasan Borivoje
Nikolic
Designing CombinationalLogic Circuits
3
Combinational vs. Sequential Logic
Combinational
Sequential
Output
(
)
f
In, Previous In
Output
(
)
f
In
4
Static CMOS Circuit
5
Static Complementary MOS
The PUN and PDN are structured in a mutually
exclusive fashion such that only one of the them
is conducting in steady-state
6
Static Complementary CMOS
- Functionally, a transistor can be thought of as
a switch. PDN is on when input signal is high and
off when low. PUN is on when signal is low and
off when high. - PDN network is constructed using NMOS while PUN
using PMOS. The primary reason for this is that
NMOS produce strong zeros while PMOS generates
strong ones, why?
7
Threshold Drops
VDD
VDD
PUN
S
D
VDD
D
S
0 ? VDD
0 ? VDD - VTn
VGS
VDD ? 0
PDN
VDD ? VTp
VGS
S
D
VDD
S
D
That is why PMOS is used in PUN, and NMOS in PDN
8
NMOS Transistors in Series/Parallel Connection
Transistors can be thought of as a switch
controlled by its gate signal NMOS switch closes
when switch control input is high
NAND
X GND Y output
NOR
9
PMOS Transistors in Series/Parallel Connection
NOR
X VDD Y output
NAND
10
Complementary CMOS Logic Style
- Number of transistors required to implement an
N-input logic gate is 2N
11
Example Gate NAND
12
Example Gate NOR
13
Complex CMOS Gate
OUT D A (B C)
14
Constructing a Complex Gate
15
OAI22 Logic Graph
A
C
XOR, XNOR ?
B
D
X (AB)(CD)
C
D
A
B
A
B
C
D
16
Properties of Complementary CMOS Gates Snapshot
- High noise margins
V
and
V
are at
V
and
GND
, respectively.
OH
OL
DD
- No static power consumption
There never exists a direct path between
V
and
DD
V
(
GND
) in steady-state mode
.
SS
- Comparable rise and fall times
(under appropriate sizing conditions)
17
Complementary MOS Properties
- Full rail-to-rail swing high noise margins
- Logic levels not dependent upon the relative
device sizes ratioless - Always a path to Vdd or Gnd in steady state low
output impedance - Extremely high input resistance nearly zero
steady-state input current - No direct path steady state between power and
ground no static power dissipation - Propagation delay as function of load capacitance
and resistance of transistors
18
Voltage Transfer Characteristics
- Multi-dimensional plot (can be obtained using DC
sweep analysis)
19
Delay Switch Delay Model
Req
A
A
NOR2
INV
NAND2
20
Input Pattern Effects on Delay
- Delay is dependent on the pattern of inputs
- Low to high transition
- both inputs go low
- delay is 0.69 Rp/2 CL
- one input goes low
- delay is 0.69 Rp CL
- High to low transition
- both inputs go high
- delay is 0.69 2Rn CL
Rn
B
21
Delay Dependence on Input Patterns
AB1?0
A1 ?0, B1
Voltage V
A1, B1?0
time ps
NMOS 0.5?m/0.25 ?m PMOS 0.75?m/0.25 ?m CL
100 fF
The difference between the later two cases of L-H
has to do with the internal node capacitance
charging
22
Transistor Sizing
The goal is to size the gate so that it has
approximately the same delay (mostly worst-case
delay) as an minimum-size inverter (9/2,3/2)
2 2
2 2
first order estimate neglecting velocity
saturation effects (smaller for stacked
transistor) and self-loading
23
(No Transcript)
24
Transistor Sizing a Complex CMOS Gate
Note the number for PMOS is with respect to PMOS
counterpart in minimum size inverter, and NMOS to
NMOS counterpart
B
3
(27/2)
3
C
3
3
OUT D A (B C)
A
2
(6/2)
D
1
B
C
2
2
25
Fan-In Considerations
A
Distributed RC model
(Elmore delay) tpHL 0.69 Reqn(C12C23C34CL)
Propagation delay deteriorates rapidly as a
function of fan-in quadratically in the worst
case.
B
C
D
C1? C2? C3? CL?
C1 CdbD, CsbC, 2CgdD, 2CgsC
26
The Elmore DelayRC Chain
27
tp as a Function of Fan-In for NAND
tp (psec)
tp
tpLH
fan-in
Gates with a fan-in greater than 4 should be
avoided.
28
tp as a Function of Fan-Out
All gates are scaled using the switched delay
model.
tpNAND2
tpNOR2
tp (psec)
tpINV
eff. fan-out
29
tp as a Function of Fan-In and Fan-Out
- Fan-in quadratic due to increasing resistance
and capacitance - Fan-out each additional fan-out gate adds two
gate capacitances to CL - tp a1FI a2FI2 a3FO
30
Fast Complex GatesDesign Technique 1
- Transistor sizing
- as long as fan-out capacitance dominates
- Progressive sizing (non-uniform sizing)
Distributed RC line M1 gt M2 gt M3 gt gt MN (the
transistor closest to the output is the
smallest)
InN
MN
In3
M3
In2
M2
Can reduce delay by more than 20 decreasing
gains as technology shrinks (due to layout)
In1
M1
31
Fast Complex GatesDesign Technique 2
- An input signal is called critical if it is the
last signal of all inputs to assume a stable
value - The path through the logic which determines the
ultimate speed of the structure is called the
critical path - Putting the critical path transistors closer to
the output of the gate can result in a speed up
32
Fast Complex GatesDesign Technique 2
- Transistor ordering
33
Fast Complex GatesDesign Technique 3
- Alternative logic structures
F ABCDEFGH
34
Fast Complex GatesDesign Technique 4
- Isolating fan-in from fan-out using buffer
insertion (inverter chains)
35
Sizing Logic Paths for Speed
- Frequently, input capacitance of a logic path is
constrained - Logic also has to drive some capacitance
- Example ALU load in an Intels microprocessor is
0.5pF - How do we size the ALU datapath to achieve
maximum speed? - We have already solved this for the inverter
chain can we generalize it for any type of
logic?
36
(No Transcript)
37
Buffer Example
In
Out
CL
1
2
N
For given N Ci1/Ci Ci /Ci-1 To find N
Ci1/Ci 4 How to generalize this to any logic
path?
38
Apply to Inverter Chain
In
Out
CL
1
2
N
tp tp1 tp2 tpN
39
Optimal Tapering for Given N
- Delay equation has N - 1 unknowns, Cgin,2
Cgin,N - Minimize the delay, find N - 1 partial
derivatives - Result Cgin,j1/Cgin,j Cgin,j /Cgin,j-1
- Size of each stage is the geometric mean of two
neighbors - each stage has the same effective fanout
(Cout/Cin) - each stage has the same delay
40
Optimum Delay and Number of Stages
When each stage is sized by f and has same eff.
fanout f
Effective fanout of each stage
Minimum path delay
41
Generalized logic path
How to size this generalized logic path?
42
Logical Effort
p intrinsic delay factor (the 2-input NAND
gate?) g logical effort f effective
fanout Normalize everything to an minimum-size
inverter with ginv 1, pinv 1 everything is
measured in unit delays tinv Assume g 1.
43
Delay in a Logic Gate with min size
Gate delay
d h p
effort delay
intrinsic delay
Effort delay
h g f
logical effort
effective fanout (of each stage) Cout/Cin
- Logical effort is a function of topology,
independent of sizing - Effective fanout (electrical effort) is a
function of load/gate size
44
Logical Effort
- Inverter has the smallest logical effort and
intrinsic delay of all static CMOS gates - Logical effort represents the fact that for a
given load, complex gate has to work harder (in
terms of transistor sizes) than an inverter to
get a similar delay). - In another way, complex gives more loading
capacitance to the previous gate when made
comparable to inverter after sizing - How much harder? How to measure it?
- Logical effort for a complex gate can be computed
from the ratio of its input capacitance to the
inverter capacitance when sized to deliver the
same current - Logical effort increases with the gate complexity
45
Logical Effort
Logical effort is the ratio of input capacitance
of a gate to the input capacitance of an
minimum-size inverter gate with the same output
current (considering worst case)
g 5/3
g 4/3
g 1
46
Logical Effort
Reference Sutherland, Sproull, Harris, Logical
Effort, Morgan-Kaufmann, 1999.
47
Logical Effort of Gates
t
pNAND
g p d
t
pINV
Normalized delay (d)
g p d
F(Fan-in)
1
2
3
4
5
6
7
Fan-out (h)
48
Logical Effort of Gates
t
pNAND
g 4/3 p 2 d (4/3)f2
t
pINV
Normalized delay (d)
g 1 p 1 d f1
F(Fan-in)
1
2
3
4
5
6
7
Fan-out (h)
Intrinsic delay is increased by twice since the
intrinsic capacitance gets two times larger
49
Logical Effort of Gates