Frequency Response Design

1
Frequency Response Design
Dr Will Browne Frequency Design CY2A2
6/1
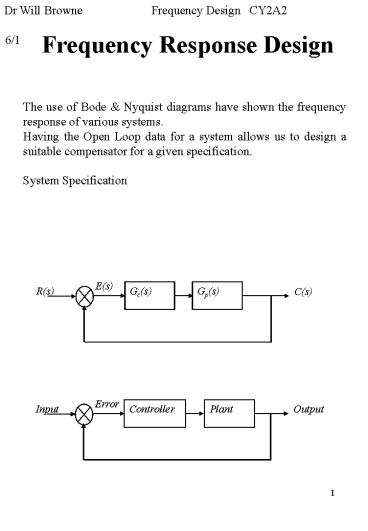
The use of Bode Nyquist diagrams have shown the
frequency response of various systems. Having
the Open Loop data for a system allows us to
design a suitable compensator for a given
specification. System Specification
E(s)
Gc(s)
Gp(s)
R(s)
C(s)
Error
Controller
Plant
Input
Output
2
Steady State Accuracy
6/2
System Specification For the above system,
the steady state error can be written as ess
lim sE(s). sgt0 The
possible inputs are Step R(t) A
Ramp R(t) At Parabola R(t) At2
E(s)
C(s)
Gc(s)
Gp(s)
R(s)
3
Steady State Errors
6/3
Looking at the steady state error for these
inputs gives where It appears that
adding more integrations 1/s (poles_at_origin) leads
to an improvement in the steady state
error. However, adding poles at the origin makes
it more difficult to stabilise the system and
also tends to add long time constants to the
transient response. To make the CL transfer
function closer to 1, the OL gain must be as
large as possible. This will decrease the errors,
but also decrease the stability of the system.
4
Transient Response
6/4

• Look at the system
• e(t) c(t)
• 1.
• 2.
• 3.
• Small time constant (T) gives fast response.

R
C
5
Transient Response
6/5

• Im
• Re
• Increased Bandwidth
• To speed up the system,
• move the poles to the left.
• This leads to an increased bandwidth.
• Thus decreasing time to peak output
• Relative Stability
• Rule of thumb.
• GM 8dB ?m 45 Usually quoted.

6
Sensitivity
6/6
The measure of the change in system
characteristics to small changes in
parameters We want this to be as small as
possible. Looking at the sensitivity s - of the
Close Loop transfer function to changes in the
plant (Gp) For the sensitivity to be
small We want a large Open Loop gain.
7
Disturbance Rejection
6/7
The disturbance is in the plant and so cannot be
dealt with by the compensator. Having a large
Open Loop gain (particularly over the frequencies
of the disturbance) will reduce the effects of
these disturbances.
8
Frequency Response Design Summary
6/8
A high Open Loop gain over a range of
frequencies gives Fast transient response.
Good sensitivity. Good tracking. Good
disturbance rejection. - Increased stability
problems.