Current Electricity and Circuits - PowerPoint PPT Presentation
1 / 47
Title: Current Electricity and Circuits
1
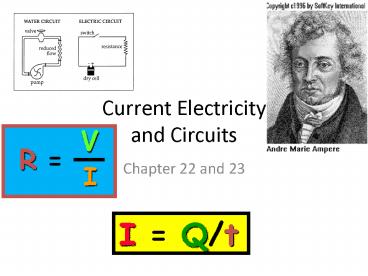
Current Electricityand Circuits
V
R
- Chapter 22 and 23
I
I Q/t
2
Electric Circuits
- Now that we have the concept of voltage, we can
use this concept to understand electric circuits - Just like we can use pipes to carry water, we can
use wires to carry electricity. - The flow of water through pipes is caused by
pressure differences, and the flow is measured by
volume of water per time
V Electrical pressure - measured in volts.
3
Electric Current
- In electricity, the concept of voltage will be
like pressure. Water flows from high pressure to
low pressure electricity flows from high
voltage to low voltage. - But what flows in electricity? Charges!
- How do we measure this flow? Current
- I DQ/Dt
- Electric current is measured in Amperes, in honor
of Andre Marie Ampere.
1 Amp 1 Coulomb per 1 second 1 C/s
4
Direction of Current Flow
- For historical reasons, current is conventionally
thought to flow from the positive to the negative
potential in a circuit. - Current flow is the rate of flow of positive
charge (Its really the electrons flowing in the
opposite direction) - Electron flow is from a lower potential (voltage)
to a higher potential (voltage). - Electrons carry negative charge
- Positive current flow is in opposite direction
5
Conventional Current
- Conventional current flows from high V to low V
and to across components like resistors. - Conventional current flows from the positive side
of the battery to the around to the negative
side. Dont be confused by diagrams that look
like it is flowing across the battery from the
negative to the positive.
I
I
-
- high V
low V R1 R2
6
Power, Current and Voltage
P W/t
Power work/time
For electric circuits,
P V .I
Power electric potential difference . current
because,
(work/charge).(charge/time)
Charge divides out leaving W/t, which is power
Electrical energy is a measure of the amount of
power used and the time of use. Electrical
energy, kilowatt hours, is the product of the
power and the time.
7
Battery or Cell Voltage Source
- A battery in an electrical circuit plays the same
role as a pump in a water system. - Because of the pumping nature of voltage
sources, we need to have a complete circuit
before we have a current. - Just like a pump needs water coming into it in
order to pump water out, so the voltage source
needs charges coming into it (into the negative
terminal) in order to pump them out (of the
positive terminal).
Does the battery or power supply actually supply
the charges that will flow through the circuit?
8
Voltage Sources
9
Symbols for Voltage Sources
- In circuit diagrams, symbols are used to
represent each component. The following symbols
may be used for voltage sources
Note The battery will be the voltage source used
in our diagrams
10
Ground
- Ground refers to the reference terminal to
which all other voltages are measured. - The earth is really just one big ground node.
- Most people choose the earth as the reference
ground when a connection to it is available.
11
Ground Symbol
12
Simple Circuit
- A simple circuit contains the minimum things
needed to have a functioning electric circuit. A
simple circuit requires three (3) things - A source of electrical potential difference or
voltage. (typically a battery or electrical
outlet) - A conductive path which would allow for the
movement of charges. (typically made of wire) - An electrical resistance (resistor) which is
loosely defined as any object that uses
electricity to do work. (a light bulb, electric
motor, heating element, speaker, etc.)
13
Ohms Law
- It takes pressure to make fluid flow due to the
viscosity of the fluid and the size of the pipe. - Voltage is required to make electric current flow
due to the resistance in the circuit. - By experiment we find that if we increase the
voltage, we increase the current V is
proportional to I. The constant of
proportionality we call the. resistance, R
14
Ohms Law
The ratio of potential difference to current is
constant.
- If R V/I is a constant value for a given
resistor, then that resistor is said to obey
Ohms Law. - Ohms Law in equation form VIR
- The SI unit of resistance is the Ohm, W, named in
honor of Georg Simon Ohm.
15
Ohms Law
16
Resistance
- The resistance depends on material and geometry
(shape). - For a wire R r L / A where where r is called
the resistivity (in Ohm-m) and measures how hard
it is for current to flow through the material, L
is the length of the wire, and A is the
cross-sectional area of the wire. - In a circuit the symbol used for resistors is
usually - In circuits, the resistance of resistors is often
given or can be calculated. The resistance of the
wire connecting the circuit is sometimes
neglected.
17
Resistance and Temperature
- Many circuit elements do not obey Ohms Law.
- Resistors that get hot, like light bulbs and
heating elements, do not keep a constant
resistance. Resistance generally increases as
objects become hotter.
18
Series and Parallel Circuits
- There are two ways devices can be connected in a
circuit, series or parallel. - Current flows differently through each type of
circuit so each requires a different set of
equations.
R1
I
V1
R2
Vbat
V2
Itotal
-
Resistors connected in series
R1
I1
Vbat
R2
I2
-
Resistors connected in parallel
19
Series Resistors - Equations
Current is constant There is only one path for
the current to take so in a series circuit,
resistance and voltage add, but current stays the
same.
1. total resistance is the sum of the
separate resistors
RT R1 R2 R3 ...
2. current is the same through each resistor
IT I1 I2 I3 ...
3. total potential difference is the sum of each
VT V1 V2 V3 ...
20
Parallel Resistors - Equations
- In a parallel circuit, resistance adds as
reciprocals, voltage stays the same, and current
splits
1. reciprocal of the total resistance is the sum
of the reciprocals of the separate resistors
1/RT 1/R1 1/R2 1/R3 ...
2. total current is the sum of the current
through each resistor
IT I1 I2 I3 ...
3. potential difference is the same across
each resistor
VT V1 V2 V3 ...
21
Kirchhoffs Current Law Junction Rule
- Kirchhoffs current law says Current into
junction Current leaving junction OR The sum of
all the currents entering a node is zero
I1 I2 I3 OR I1 I2 I3 0
node
Io
How much is the current Io , if I2 is 2.5 mA and
I3 is 4 mA?
22
Kirchhoffs Current Law applies to all types of
networks
Fiber optic network (I is light intensity)
I1
I2
KCL for light
I1 I2 I3
I3
23
Kirchhoffs Current Law applies to all types of
networks
Human Blood Vessels (f is blood flow rate)
f2
f1
f1
KCL for blood flow
f1 f2 f3
f3
24
Kirchhoffs Voltage Law Loop Rule
- Kirchhoffs Voltage Law Sum of all voltage drops
and voltage rises in a circuit (a closed loop)
equals zero OR The voltage measured between any
two nodes does not depend of the path taken.
V1 V2 V3
V1 V2 V4
V3 V4
25
Kirchhoffs Voltage Law Loop Rule
Kirchhoffs Voltage Law V1 V2 V3
OR
V1 V2 V3 0
26
Using the Loop Rule
- Assign symbols and directions of currents in the
loop - If the direction is chosen wrong, the current
will come out with a right magnitude, but a
negative sign (its ok). - Choose a direction (cw or ccw) for going around
the loop. Record drops and rises of voltage
according to this - If a resistor is traversed in the direction of
the current -V -IR - If a resistor is traversed in the direction
opposite to the current VIR - If EMF is traversed from to E
- If EMF is traversed from to -E
27
Using the Loop Rule
- Loops can be chosen arbitrarily. For example, the
circuit below contains a number of closed paths.
Three have been selected for discussion.
Suppose that for each element, respective current
flows from to - signs.
-
-
v2
v5
Path 1
-
-
-
v1
v4
v6
Path 2
v3
v7
-
-
Path 3
-
v8
v12
v10
-
-
-
-
v11
v9
28
Using the Loop Rule
b
Using sum of the drops 0
-
-
v2
v5
-
-
-
Blue path, starting at a - v7 v10 v9 v8
0
v1
v4
v6
v3
v7
-
-
a
Red path, starting at b v2 v5 v6 v8
v9 v11 v12 v1 0
-
v8
v12
v10
-
-
Yellow path, starting at b v2 v5 v6 v7
v10 v11 - v12 v1 0
-
-
v11
v9
29
Using the Loop Rule
- Example For the circuit below find I, V1, V2,
V3, V4 and the power supplied by the 10 volt
source.
- For convenience, we start at point a and sum
voltage drops 0 in the direction of the current
I.
2. We note that V1 - 20I, V2 40I, V3
- 15I, V4 5I (2)
3. We substitute the above into Eq. 1 to obtain
Eq. 3 below.
10 20I 30 15I 5I 20 40I 0
(3)
Solving this equation gives, I 0.5 A.
30
Using the Loop Rule
Using this value of I in Eq. 2 gives
V1 - 10 V
V3 - 7.5 V
V2 20 V
V4 2.5 V
P10(supplied) -10I - 5 W
(We use the minus sign in 10I because the
current is entering the terminal) In this case,
power is being absorbed by the 10 volt supply.
31
P, W
V, V
R, W
I, A
E 12 V
8.0
R1
2.0
R1
R3
R2
5.0
R3
RT
R2
VT
IT
PT
32
P, W
V, V
R, W
I, A
E 12 V
8.0
R1
0.80
6.4
5.1
2.0
0.80
1.6
1.3
R1
R3
R2
5.0
0.80
4.0
3.2
R3
RT 15 ?
R2
VT 12 V
IT 0.80 A
PT 9.6 W
33
P, W
R, W
V, V
I, A
E 12 V
12
R1
8.0
R2
R1
12
R3
R2
RT
R3
VT
IT
PT
34
P, W
R, W
V, V
I, A
E 12 V
12
12
1.0
12
R1
1.5
8.0
12
18
R2
R1
12
1.0
12
12
R3
R2
RT 3.42 ?
R3
VT 12 V
IT 3.50 A
PT 42 W
35
Toll Road Circuit Analogy
Adding toll booths in series increases resistance
and slows the current flow. Adding toll booths
in parallel lowers resistance and increases the
current flow.
36
Combined Series parallel circuits
- Rt R1 1/(1/R2 1/R3) add R2 and R3 as
parallel then add the result to R1 - Vt V1 (V2 V3)
- It I1 I2 I3 total current goes through R1
but splits when it go through R2 and R3
37
Internal Resistance
Real batteries are constructed from materials
which possess non-zero resistance. It follows
that real batteries are not just pure voltage
sources. They also possess internal resistances.
A battery can be modeled as an emf connected in
series with a resistor , which represents its
internal resistance.
38
Capacitor /Water Tower
- A water tower holds water. A capacitor holds
charge. - While we normally define the capacity of a water
tank by the TOTAL AMOUNT of water it can hold, we
define the capacitance of an electric capacitor
as the AMOUNT OF CHARGE PER VOLT instead. C Q/V - There is a TOTAL AMOUNT of charge a capacitor can
hold, and this corresponds to a MAXIMUM VOLTAGE
that can be placed across the capacitor. Each
capacitor DOES HAVE A MAXIMUM VOLTAGE. - If an electric capacitor is over-filled or
equivalently a higher voltage is placed across
the capacitor than the listed maximum voltage It
will break by having the charge escape. This
escaping charge is like lightning - a spark that
usually destroys the capacitor
39
Capacitors In Series
- There is only one way around the circuit, and you
have to jump BOTH capacitors in making the
circuit - The positive charge on the left plate of C1 will
attract a negative charge on the right plate, and
the negative charge on the bottom plate of C2
will attract a positive charge on the top plate -
just what is needed to give the negative charge
on the right plate of C1.
C1
(Q1 ? )
Q1 -Q 1
Q2
V
C2
-Q2
( ? Qtotal)
Vtotal (V1 V2)
1/C1 1/C2 1/Ceffective
Qtotal Q1 Q2
40
Capacitors Parallel
- For parallel, both plates are across the same
voltage, so Vtotal V1 V2 . The charge can
accumulate on either plate, so Qtotal (Q1
Q2). - Since the Qs are in the numerator, we have
Ceff C1 C2.
Q1
Q2
C1
C2
V
-Q1
-Q2
Q1 ?
? Qtotal (Q1Q2)
? Q2
41
The Light Bulb and its Components
- Has two metal contacts at the base which connect
to the ends of an electrical circuit - The metal contacts are attached to two stiff
wires, which are attached to a thin metal
filament. - The filament is in the middle of the bulb, held
up by a glass mount. - The wires and the filament are housed in a glass
bulb, which is filled with an inert gas, such as
argon.
42
Light bulbs and Power
- Power dissipated by a bulb relates to the
brightness of the bulb. The higher the power,
the brighter the bulb. - Power is measured in Watts W
- Power, P IV, can also be written P I2R or P
V2 / R by using Ohms law and doing some
substitutions. - If we wanted a higher power light bulb, should we
have a bigger resistance or a smaller resistance
for the light bulb?
43
Light bulbs and Power - Answer
- Answer In this case, the voltage is being held
constant due to the nature of the batteries.
This means that the current will change as we
change the resistance. Thus, the P V2 / R
would be the most straight-forward equation to
use. This means that as R goes down, P goes up.
(If we had used the P I2R formula, as R goes
up, I would decrease so it would not be clear
what happened to power.) - The answer for more power, lower the
resistance. This will allow more current to flow
at the same voltage, and hence allow more power!
44
Light bulbs and Power
- The three light bulbs in the circuit all have the
same resistance. Given that brightness is
proportional to power dissipated, the brightness
of bulbs B and C together, compared with the
brightness of bulb A, is - 1. twice as much.
- 2. the same.
- 3. half as much.
45
RC circuits
- When switch is closed, current flows because
capacitor is charging - As capacitor becomes charged, the current slows
because the voltage across the resistor is ? - Vc
and Vc gradually approaches ?. - Once capacitor is charged the current is zero
q
q
Charge across capacitor
RC is called the time constant
46
RC circuits
- If a capacitor is charged and the switch is
closed, then current flows and the voltage on the
capacitor gradually decreases. - This leads to decreasing charge
q
Charge across capacitor
0.37q
47
Sources
- www.physics.ubc.ca/outreach/phys420/p420_04/mitsuk
o/OhmsLaw-Gr10-Science.ppt - http//physics.bu.edu/duffy/PY106
- Physics by Zitzewitz
- www.glenbrook.k12.il.us/GBSSCI/PHYS/Class
- www.cbu.edu/jholmes/P202/P1elec2.ppt























![L 27 Electricity and Magnetism [4] PowerPoint PPT Presentation](https://s3.amazonaws.com/images.powershow.com/7347050.th0.jpg?_=20151107026)






