Repr

1
Représentations temps-fréquenceet temps-échelle
ETASM 2007

• Jérôme Mars, Professeur, GIPSA-Lab
• Institut National Polytechnique de Grenoble

2
Les signaux stationnaires

• Signal représenté en temps OU en fréquence
• Temps Fréquence
• Amplitude Forme donde x(t) Amplitude complexe
  X(f)
• Énergie Corrélation Cx (t) DSP Sx (f)
• La fonction de corrélation
• ? DSP par WK
• Les différents types de classes
• Temps/fréquence Continu Discret
• Continu x(t) X(f) x(n)
  X(z),X(l)
• Cx(t) Sx(f) Cx(k) Sx(z) Sx(l)
• Discret x(te) X(m) x(n) X(m)
• Cx(t) Sx(m) 0ltnltN

TFr TZ
TF
TF
TFD
3
Les différentes bases

• Représentation Base associée
• Temps continu Dirac continus d(q - t) avec q,
  t ??
• Temps discret Dirac discrets d(n - k) avec
  n, k ??
• Fréquence continue Expo. infinie exp(-2ipft)
  avec t,f ??
• Fréquence réduite Expo. discrète exp(-2iplnt)
  
• avec n??, l?-1/2,1/2
• Temps et fréq. discrets Expo. de période N
  exp(-2ipnm/N)
• avec n,m ?0,N-1

Ces bases sont importantes car elle permettent de
comprendre physiquement la dualité temps et
fréquence
4
Rappel sur la TFD

TFD
avec 0 lt m lt N
TFD-1
avec 0 lt n lt N
Avec qb.N 1 Selon le cas on pose q1 ? b
1/N ou b 1 ? q 1/N Pour retrouver les
valeurs  vraies  on pose qTe ? b
1/NTe Nte durée du signal et b écart de
fréquence entre 2 canaux
5
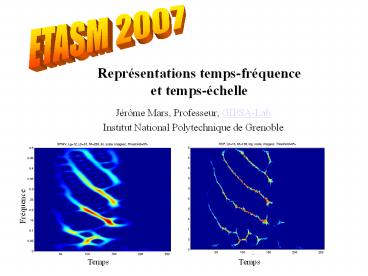
Exemples
?
?
Question Caractéristiques fréquentielles ?
Df, Te1, N en f Qui arrivent en premier
BF ou HF ? Unicité de la TF ?.
6
Exemples
Question Qui arrivent en premier
? Unicité de la TF (Oui)
7
Problèmes liés aux signaux stationnaires

• Les représentations temporelles (t ou t) ne font
  pas apparaître la répartition fréquentielle..
• Les représentations fréquentielles ne permettent
  pas une datation des évènements
• Les DSP donnent une description correcte de la
  répartition fréquentielle de lénergie des
  signaux stationnaires dont les propriétés sont
  invariantes avec le temps.
• Les propriétés des signaux non stationnaires
  dépendent du temps.
• on souhaite faire lanalyse en fréquence de
  régions locales du signal .i.e. localisée
  temporellement.
• ? ANALYSE TEMPS- FREQUENCE

8
Les signaux non stationnaires

• Un signal dont la  structure  change au cours
  du temps (TF ?)
• parole, musique, impacts,  chirp , machines
  tournantes
• QQ exemples
• COMMUNICATION
• Animaux communicants
• MUSIQUE

9
MEDECINE

10
RECONNAISSANCE BIOMETRIQUE
Ex Détection d'insectes xylophages par contrôle
non destructif

• MEDECINE

11
DIAGNOSTIQUE DE MACHINES
Signal dengrenage

• MEDECINE

• La partie non stationnaire Changement de régime
  ou incident.
• Information non stationnarité

12
Signaux Naturels
Reconnaissance, Sonar Naturel
13
EXEMPLES SONORE

• Signaux utilisés en communication
• En électronique (Radar Sonar)
• En détection de cibles,

14
EXEMPLES SONORE

• Signaux utilisés en communication
• Signaux sonores
• Exemples sont excessivement nombreux
• Médecine, Biométrie,
• Mécanique, Contrôle non destructif
• Gestion de la biodiversité et de lenvironnement

15
La fonction dautocorrélation et DSP

• Aléatoire stationnaire
• Aléatoire , non stationnaire

16
PLAN DU COURS

• Intro Relation dincertitude temps fréquence.
• CHAPITRE 1 Méthodes inspirées de  Fourier 
• Représentation temps-fréquence instantanée
  illustrations
• Cadre général des représentations temps
  fréquence constitué par Les représentations de
  Wigner-Ville et par les fonctions dambiguïté
• Spectrogramme (loutil le plus répandu)
  illustrations
• CHAPITRE 2 Méthodes basées sur des
  modélisations
• Méthode paramétrique (AR, Pisarenko, Prony)
• Méthode basé sur un banc de filtre (Capon,
  Lagunas)

17
PLAN DU COURS

• -Intro Relation dincertitude temps fréquence.
• CHAPITRE 1 Méthodes inspirées de  Fourier 
• Représentation temps-fréquence instantanée
  illustrations
• Cadre général des représentations temps
  fréquence constitué par LES représentationS de
  Wigner-Ville et par les fonctions dambiguïté
• Spectrogramme (loutil le plus répandu)
  illustrations
• CHAPITRE 2 Méthodes basées sur des
  modélisations
• Méthode paramétrique (AR, Pisarenko, Prony)
• Méthode basé sur un banc de filtre (Capon,
  Lagunas)

18
Le principe dincertitude temps-fréquence

• Les relations dHeisenberg Gabor (1946)
  interdisent à un signal davoir une localisation
  arbitrairement précise en temps et en fréquence.
• plus on veut se localiser sur une portion dun
  signal
• moins on peut spécifier les fréquences
  précisément
• Dirac temporel (localisé en temps, délocalisé en
  fréquence)
• A lopposé de
• Pour localiser de manière précise un signal en
  temps et en fréquence, on souhaiterait que sa
  durée T et sa largeur de bande tendent
  simultanément vers 0. (BT ? 0) ?.

19
Le principe dincertitude temps-fréquence

• Approche mathématique
• Un temps central (instant moyen) Une
  fréquence centrale (freq. c).
• Une durée T (épanouissement) Une largeur de
  bande B
• Le principe dincertitude est

20
Le principe dincertitude temps-fréquence

• On ne peut pas localiser en temps et en fréquence
  de façon précise en même temps.
• Si lt Dt gt ? 0 , alors lt Df gt ? ? (cf Dirac)
• Si lt Df gt ? 0 , alors lt Dt gt ? ? (cf. fréquence
  pure)
• Il existe des signaux qui atteignent la borne
  inférieure du produit BT (Ce sont des logons
  daprès Gabor ou  gaborettes daprès les
  autres).
• Tout ceci est conforme à une vision intuitive des
  choses
• Pour mesurer une fréquence, il faut lobserver
  sur une durée
• Un signal bref ne donne aucune info sur le
  spectre

21
De Gabor au pavage dans le plan temps-fréquence

• Au mieux à laide des gaborettes, en les
  translatant, on peut partager le plan
  temps-fréquence en localisant au mieux
  lénergie..
• Ce partage découpe le plan temps-fréquence en
  rectangle dont laire est fixée lt Dt . Df gt
  .mais on peut faire varier cette forme

22
Décomposition du plan temps-fréquence

• Base temps h(t) ? Base Fourier h(t)?
• Base Fourier
  h(t-u)

Fréquence
Fréquence
Temps
Temps
Fréquence
Temps
23
PLAN DU COURS

• Intro Relation dincertitude temps fréquence.
• CHAPITRE 1 Méthodes inspirées de  Fourier 
• Représentation temps-fréquence instantanée
• Cadre général des représentations temps
  fréquence constitué par Les représentations de
  Wigner-Ville et par les fonctions dambiguïté
• Spectrogramme (loutil le plus répandu)
  illustrations
• CHAPITRE 2 Méthodes basées sur des
  modélisations
• Méthode paramétrique (AR, Pisarenko, Prony)
• Méthode basé sur un banc de filtre (Capon,
  Lagunas)

24
Temps-fréquence instantanée ou Comment définir
une fréquence ?

• Dans le cas stationnaire
• Fourier
•  Sinusoïde de durée infinie 
• Dans le cas non stationnaire
• même définition que le cas stationnaire mais QUI
  VARIE DANS LE TEMPS??
• Impossible à cause du principe dincertitude
• On définit alors la FREQUENCE INSTANTANEE
• Ou REPRESENTATION TEMPS-FREQUENCE INSTANTANEE
• (Ville 1948)

25
Représentation temps-fréquence instantanée
Définition.

• Def. à partir dun signal réel x(t), on
  construit le signal analytique
• avec y(t) la T. Hilbert de x(t).
• Le signal complexe décrit de manière unique une
  paire mod-phase.
• Amplitude instantanée
  Enveloppe du signal
• Fréquence instantanée Dérivée de la phase
• RTF instantanée graphe de
• Vecteur tournant module et phase variable au
  cours du temps

Re z(t)
TFy(t) -i sign(f) Y(f)
26
RTF instantanée exemple
27
RTF instantanée Mise en œuvre (1)

• 2 types de programmation Analogique ou
  numérique
• 1-Analogique (Berthomier 1972) Filtre en
  quadrature (pas adapté).
• 2-Numérique temps discret.
• Avec N nb. échantillon, X(m)TFDx(n) et
  Z(m)TFDz(n)
• On déduit le
  module et la phase
• Problème de déroulement de phase

28
RTF instantanée Mise en œuvre (2)

• Déroulement de la phase .
• Phase est définie à 2 ? près.apparition de
  discontinuités
• Restitution dune phase  continue  avant le
  calcul de la freq. Inst.
• Méthode Dérouler la phase..
• Approcher la fréquence instantanée par
• en
  réduit. -?

29
Information duale Retard de groupe

• Fréquence instantanée
• x(t) cos(2?f0t)
• zx (t) cos(2?f0t) j. sin(2?f0t) e2j?f0t
• fi(t) 1/2?. d/dt arg (zx(t) f0
• localisation en fréquence dune composante
  temporelle
• Retard de groupe tg
• Zx(f) TF zx(t)
• tg 1/2?. d/df Arg Zx(f) Retard de groupe
• x(t) cos (2?f0.t), zx (t) e2j?f0t
• Zx (f) ?(f-f0) ? tg 0
• x(t) cos (2?f0(t-t0)), zx (t) e2?f0(t-t0)
• Zx (f) ?(f-f0).e- 2?t0 ? tg t0
• localisation en temps dune composante
  fréquentielle

30
RTF instantanée Exemple MONOCOMPOSANTETEMPS R
TF Instantanée
Signal 1 Fréquence pure 0.1 Hz
Signal 2 Fréquence pure 0.3 Hz
31
RTF instantanée Exemple MULTI COMPOSANTE
Signal 12 Fréquence pure 0.1 0.3 Hz
32
RTF instantanée MONO COMPOSANTE BRUIT
Représentation temporelle
Signal 1 (0.1 Hz) bruit (0 db)
RTF Instantanée
33
RTF instantanée Conclusion

• La RTF instantanée est une méthode capable de
  décrire finement les propriètes temporelles et
  fréquentielles de signaux appartement à une
  CLASSE LIMITEE
• CLASSE LIMITEE SIGNAUX MONOCOMPOSANTE
• Pour lequel à un instant (une fréquence) le
  signal nexiste quautour dune fréquence
  (respectivement un instant).
• Dans le cas contraire (multicomposante), la
  valeur obtenue est erronée combinaison des
  valeurs.
• Mauvais comportement au bruit. Analyse
  demandée

34
RTF instantanée ONDE DE LOVE
RTF Instantanée
35
PLAN DU COURS

• Intro Relation dincertitude temps fréquence.
• CHAPITRE 1 Méthodes inspirées de  Fourier 
• Représentation temps-fréquence instantanée
• Représentation de Wigner-Ville et ses dérivées
• Spectrogramme (loutil le plus répandu)
  illustrations
• CHAPITRE 2 Méthodes basées sur des
  modélisations
• Méthode paramétrique (AR, Pisarenko, Prony)
• Méthode basé sur un banc de filtre (Capon,
  Lagunas)

36
Représentation temps fréquence
37
Représentation de Wigner-Ville

• La représentation de Wigner-Ville (Wigner 1932
  Ville 1948)
• En continu
• Interprétation en rouge Corrélation
  instantanée dépendant du tps.
  une Tf sur le retard t ? DS instantanée
  ON PREND
  TOUT LE SIGNAL
• Dualité

38
Qq. Propriétés de la TF de Wigner-Ville (1)

39
Wigner Ville cas discret

• Lindice l, dans la TFWV directe correspond à
  l.?t/2
• Lindice k, dans la TFWV inverse correspond à
  k/2.M.?t
• D où un échantillonnage 2 fois plus fin!
• Autre interprétation
• le produit des 2 signaux x(t), x(tT/2) donne
  dans le domaine fréquentiel une convolution avec
  un spectre de largeur double! D où la nécessité
  d échantillonner à une fréquence double de celle
  de Nyquist!

40
Représentation Wigner-Ville
Signal 1 Fréquence pure 0.3 Hz Exo !!! WV
dun Dirac, dune modulation
41
Les interférences

• La représentation de Wigner-Ville introduit des
  artéfacts pour des signaux multicomposantes
  (plusieurs contributions fréquentielles).
• Somme x(t) y(t)
• Avec
• Pour un signal à N composantes ? N(N-1)/2
  composantes
• Composer Termes propres et dartéfactqui ont
  souvent une structure oscillante dépendante des
  écarts temporels et fréquentiels des
  composantes.

42
Structures des Interférences
43
Propriétés de la TF de Wigner Ville(2)

• Inconvénients
• Valeurs négatives locales !!!
• Interférences entre les composantes des signaux
• ceci est du au produit x(t-T/2) x(tT/2)
• Avantages
• meilleure résolution en temps et fréquence
  puisque on utilise tout le signal
• estimation des modulations de fréquences
• du retard de groupe

44
Transformée de Wigner VilleUtilisation du signal
analytique

• Au lieu d utiliser x(t), on utilise le signal
  analytique de x(t)
• Ce signal a un spectre défini uniquement pour les
  fréquences positives.
• Ce permet
• déviter d échantillonner à la fréquence double!
• déviter les interactions entre les fréquences
  positives et négatives du spectres.
• Formulation basée sur la TF des signaux
• Remarque
• il n y a pas de pertes d informations
• WV est défini pour les fréquences positives, sans
  pertes d informations

45
Pseudo Wigner-Villeet Pseudo Wigner-Ville Lissé

• Pseudo Wigner Ville lissage en fréquence
• version lissée en fréquence convolution par une
  fonction F localisée au voisinage de lorigine
  des temps et des fréquences
• on utilise une portion du signal
• moins bonne résolution en fréquence.
• Pseudo Wigner Ville Lissé lissage en temps et
  fréquence
• convolution bi-dimensionnelle
• réduction des interférences
• positivité
• perte de résolution T-F

46
Dérivées de Wigner Ville quelques conclusions

• Utilisation du signal analytique préférable
• Utilisation de la Pseudo Wigner Ville Lissé
• Convolution bi-dimensionnelle
• Diminution des Interférences
• Positivité
• Perte de résolution Temps et fréquence (double
  convolution)
• Efficace sur des structures  sinusoidale 
• Nombreuses applications (méca, automobile
  détection etc)
• Nombreuses littératures (Flandrin etc)

47
La distribution de Wigner Ville et la fonction
dambiguïté

• Ambiguïté outil très important dans la
  communauté Radar
• Mesure de ressemblance dun signal avec ses
  translatées en temps et en fréquence (doppler)
• En temps
• En fréquence
• Dualité WV ? ? Ambiguïté

48
La distribution de Pseudo Wigner Ville et la
fonction dambiguïté

• Lissage (par convolution) de la WV
  multiplication (apodisation) de la fonction
  dambiguïté par double TF de la fonction de
  lissage.
• avec
• Le lissage peut se faire dans le domaine (t,n)
  par convolution ou dans le domaine (t,f) par
  apodisation.
• Les termes propres seront localisés au voisinage
  de lorigine.
• Les termes dinterférence seront éloignés de
  lorigine.

49
La fonction dambiguïté (exemple)
50
Distribution de Wigner Ville et fonction
dambiguïté

• Signaux déterministes Signaux aléatoires
• Ces estimateurs sont non biaisés ..
• La variance de ces estimateurs est importante.
  Comme lestimateur de la corrélation,
  lestimateur de  a une variance faible au
  voisinage de lorigine et forte dans le cas
  contraire. Les termes lointains étant apodisés,
  on obtient une réduction des fluctuations
  statistiques.

51
Distribution de Wigner Ville et fonction
dambiguïtéConclusion

• La représentation de Wigner Ville prend en compte
  TOUT le signal.
• Pour les signaux déterministes gt Représentation
  de WV
• Pour les signaux aléatoires gt Spectre de WV
• Utilisation de la Pseudo Wigner Ville Lissé
• Convolution bi-dimensionnelle
• Diminution des Interférences pour les signaux
  déterministes
• Diminution de la variance pour les signaux
  aléatoires.
• Perte de résolution temps et fréquence (double
  convolution)

52
Distribution de Wigner Ville examples
On peut adapter la fonction de pondération à la
structure des signaux.
53
PLAN DU COURS

• Intro Relation dincertitude temps fréquence.
• CHAPITRE 1 Méthodes inspirées de  Fourier 
• Représentation temps-fréquence instantanée
• Wigner-Ville et par les fonctions dambiguïté
• Spectrogramme (loutil le plus répandu)
• CHAPITRE 2 Méthodes basées sur des
  modélisations
• Méthode paramétrique (AR, Pisarenko, Prony)
• Méthode basé sur un banc de filtre (Capon,
  Lagunas)

54
Le spectrogramme formulation

• Short Time Fourier Transform basé sur la TF de
  segments stat.
• en continu
• avec A
• h(t) est une fenêtre glissante de durée D qui
  fixe la durée des seg.
• bonne résolution temporelle si h(t) courte
• bonne résolution fréquentielle si h(t) longue
• en discret

55
Décomposition du plan temps-fréquence

• Base temps h(t) ? Base Fourier h(t)?
• Base Fourier
  h(t-u)

Fréquence
Fréquence
Temps
Temps
Fréquence
Temps
56
Pseudo Wigner Ville Lissé et Spectrogramme

• Spectrogramme
• Interprétation
• le spectrogramme correspond à une version lissée
  de WV

WV du signal
WV de la fenêtre
57
Spectrogramme Mise en oeuvre

• Fenêtre de taille 2n (TFD rapide) .. Cf. choix
  de la longueur de N
• Type de fenêtre (Hanning, Hamming, Blackman
  Harris, .sauf rectangulaire (lobe principal
  large mais lobes secondaire atténués).
• Temps de décalage (1 échantillon ? redondance
  (Demi longueur de fenêtre ?
  classique).
• Zéro-padding parfois nécessaire au début et à la
  fin .
• Réglage de la moyenne sur chaque fenêtre
• Visualisation de différent types (échelle
  linéaire ou log)
• Périodogramme moyenné si nécessaire.

58
Choix de la durée des segments

• Pour fixer N (le nb. déchantillon qq règles sont
  nécessaires) en fonction du degré de non
  stationnarité.
• Pour un signal variant lentement, on peut
  prendre une longue durée
• Inversement pour un signal à variation rapide..
• Soit un signal monocomposante dont la fréquence
  varie selon la loi
• avec la vitesse de variation
  de fréquence.
• La bande passante occupée par la TF dun segment
  est
• avec la bande passante intrinséque
  du segment de durée D
• et
  , la bande parcourue par le signal pd D
• La durée D  optimale est celle qui minimise la
  bande B soit
• Et la précision en fréquence est
• 
  
• Cas discret
• Cas limite fréquence pure ? a 0 ?durée
  optimale infinie (stationnaire)
• dirac a ? ?durée optimale
  nulle

59
Le spectrogramme
?
60
Effet de la taille de fenêtre (de Hanning)
8 Points
16 Points
32 Points
64 Points
128 Points - lin
128 Points - Log
61
Le spectrogramme. Quelques propriétés

• Les plus
• positif,
• extension directe de Fourier, interprétation
  identique en fréquence
• pas de termes dinterférences
• Les moins
• principe dincertitude BT? 1/2,
• compromis entre résolutions en fréquence et en
  temps
• la résolution et les lois en fréquence sont
  fonction de la fenêtre
• l optimisation des fenêtres nécessite des
  informations a priori sur le signal

62
Spectrogramme double chirp (nfft128)
63
Spectrogramme double chirp (nfft256)
64
Spectrogramme double chirp (nfft512)
65
Spectrogramme signal d engrenage (nfft256)
66
Spectrogramme signal d engrenage (nfft1024)
67
Pseudo WV signaux d engrenage nfft256
68
Cas particuliers de la classe de Cohen

• Forme générale

69
PLAN DU COURS

• Intro Relation dincertitude temps fréquence.
• CHAPITRE 1 Méthodes inspirées de  Fourier 
• Représentation temps-fréquence instantanée
  illustrations
• Cadre général des représentations temps
  fréquence constitué par LES représentationS de
  Wigner-Ville et par les fonctions dambiguïté
• Spectrogramme (loutil le plus répandu)
  illustrations

70
CHAPITRE 2 RTF  paramétriques 

• Les RTF issue de Fourier
• banc de filtre à bande passante constante suivi
  dune estimation de la puissance méthode FQI
  (filtrage Quadration Intégration)
• Il existe 2 autres familles
• 1) Fondée sur lidentification dun modèle de
  signal (AR ou entropie max, méthode de pisarenko,
  méthode de Prony)
• 2) Fondée sur la mise en œuvre dun filtre passe
  bande adapté au signal traité Méthode de Capon
  et ses dérivées
• Ces méthodes sont développées pour les signaux
  stationnaires. Elles sont adaptées aux signaux
  non stationnaires par adaptation dune fenêtre
  glissante.

71
Vue générale

• Le signal x(n) que lon analyse est connu sur M
  avec
• A partir de ces M échantillons, on obtient
  pour avec PltM
• Pour les signaux non stationnaires
• dépendant de linstant n et du retard k.
• La corrélation complète
• Cor. pour des
  retards
• La densité spectrale
• Problème ??? Comment résoudre ceci
• Solution Méthodes paramétriques consistent à
  fixer et
  en se donnant un modèle
  du signal

72
Méthode du modèle Autorégressif

• On suppose que le signal observé dont la
  connue sur P retards est la sortie
  dun filtre AR dordre P excité par un bruit
  blanc b(n)
• Il faut déterminer les P coef. ai(n) et la
  puissance du bruit blanc Pb(n).
• On dispose de P1 valeurs de corrélation pour
• Le modèle sera adapté au signal si lerreur de
  prédiction b(n) est petite
• Connaissance de P et seuil à définir

Erreur de préd.
Prédiction à partir des P valeurs précédents
73
Identification dun filtre AR

• En multipliant les équations par
• En prenant E et en notant que
• on obtient les équations de Yule-Walker
• Ces relations permettent didentifier le filtre
  AR et de calculer la puissance du bruit blanc ..
  Résolution par différentes méthodes (Levinson
  etc.)

74
Identification dun filtre AR

• Sous une forme vectorielle cela revient à
  minimiser une puissance derreur
  
• avec et
  la matrice de corrélation (P1, P1) de x(n).
• La puissance derreur est minimisée sous la
  contrainte
• La solution (multiplicateur de Lagrange) de ce
  problème est
• La
  solution est

75
Mise en oeuvre

• Pour obtenir une image temps-fréquence dans le
  cas non stationnaire
• Il faut estimer les coef. du filtre AR associé à
  un nombre P (nb de pôle) préalablement définie
  par le user sur une fenêtre ou mémoire glissant.
• (stationnarité nécessaire).
• Les deux paramètres importants sont P Nb de
  pôles et N longueur de fen.
• Le nombre de pôles Ordre de filtre (fonction du
  nb. de composante).
• Longueur de fenêtre 2 et 5 fois P.
• Longueur inférieure à celles des fenêtres
  utilisées pour le spectrogramme.
• Exemple Pour une seule fréquence pure 1 pole
  et son conjugué ? P2.

76
3 façons destimateur temps-fréquence AR (1)

• RTF AR énergétique
• La RTF
• RTF AR par les maximas
• Les valeurs de la puissance sont peu fiables.
• Les valeurs de la localisation des composantes
  par le maxima des dsp du modèle AR sont de bonne
  qualité.
• Le graphe est de même qualité que la RTF
  Instantanée
• Mais on préfère la RTF par les pôles

77
3 façons destimateur temps-fréquence AR (2)

• RTF AR polaire
• Possibilité dutiliser un diagramme polaire
  directement issu du calcul des pôles du filtre
  autorégressif. Après estimation des pôles, il est
  possible de calculer la fréquence associée à
  chaque pôle dans le plan complexe.

78
Exemple Synthétique

Ps
Pe
79
Exemple Synthétique

A
B
RTF DSP
RTF Polaire
6 Poles et L24
Ps
Pe
80
Exemple Synthétique bruité

RTF DSP
8 Poles et L32
B
RTF Polaire
Ps
Pe
81
PLAN DU COURS

• Intro Relation dincertitude temps fréquence.
• CHAPITRE 1 Méthodes inspirées de  Fourier 
• Représentation temps-fréquence instantanée
  illustrations
• Cadre général des représentations temps
  fréquence constitué par LES représentationS de
  Wigner-Ville et par les fonctions dambiguïté
• Spectrogramme (loutil le plus répandu)
  illustrations
• CHAPITRE 2 Méthodes basées sur des
  modélisations
• Méthode paramétrique (AR, Pisarenko, Prony)
• Méthode basé sur un banc de filtre (Capon,
  Lagunas)

82
La méthode de Capon Objectif

• Principe
• Construction dun filtre passe bande autour dune
  fréquence fk sous 2 contraintes.
• 1 Restituer sans erreur la puissance du signal à
  la fréquence fk
• 2 Rejeter au mieux les parasites formés par les
  autres fréquences et le bruit.
• 1 Spectre à la fréquence fk ne doit pas être
  altéré. Puissance de Sortie Puissance dentrée
  pour la fréquence fk.
• 2 Minimisation des interférences dues aux autres
  fréquences.

83
La méthode de Capon Description

• Filtre de Capon Filtre à moyenne mobile ?
• avec lentrée du filtre aux instant
  n-p.
• avec le vecteur des
• coef. du filtre extrayant la composante de
  la fréquence l
• Le vecteur décrivant la composante à la fréquence
  l.
• La sortie du filtre de Capon

84
La méthode de Capon Description

• Pour conserver la puissance de la composante on
  doit vérifier
• La puissance du filtre de Capon est
• La réponse impulsionnelle, du filtre de
  capon est donnée par les deux conditions
• Minimisation sous contrainte (Lagrange )
• ? réponse impulsionnelle

85
La RTF issue de Capon

• La RTF issue de Capon est
• Cet estimateur est homogène à une puissance. Un
  filtre est construit à chaque fréquence de la
  bande passante du signal. Le filtre estimé est
  donc adapté au signal à chaque fréquence.
• Une fenêtre glissante ou mémoire glissante sur la
  durée totale du signal permet dobtenir la DSP
  adaptée.
• Paramètres dutilisation Taille de la fenêtre
  et Ordre du filtre (idem que AR)

86
La méthode de Lagunas et ses dérivées..

• Normalisation / bande passante
• La puissance de
• sortie du filtre
• Avec le gain complexe du
  filtre, la dsp du signal au tps
  n.
• Si le filtre a une bande passante étroite,
• Parceval permet de dire

87
Example Capon

88
RTF Paramétriques Conclusion

• Résolution meilleure que les PWVL et
  Spectrogramme.
• AR Estimateur fréquentielle très bon (surtout
  avec la représentation polaire). Mauvais
  estimateur de puissance..
• Capon Estimateur de puissance, mauvais
  estimateur en fréquence .
• Extension à Lagunas permet davoir cette
  estimateur de puissance.
• Possibilité de coupler AR-CAPON et/ou LAGUNAS
  CAPON
• permettant davoir à la fois un bon
  estimateur en fréquence et en puissance.
• Paramétrage ! Connaissance du nombre de
  fréquences recherchées nécessaire.. (Ordre du
  Filtre, Longueur entre 3 et 5 P).