ThemeGallery PowerTemplate - PowerPoint PPT Presentation
Title:
ThemeGallery PowerTemplate
Description:
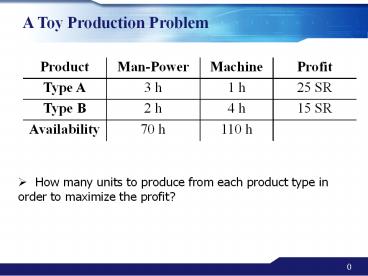
A Toy Production Problem Product Man-Power Machine Profit Type A 3 h 1 h 25 SR Type B 2 h 4 h 15 SR Availability 70 h 110 h How many units to produce from each ... – PowerPoint PPT presentation
Number of Views:125
Avg rating:3.0/5.0
Title: ThemeGallery PowerTemplate
1
A Toy Production Problem
Product Man-Power Machine Profit
Type A 3 h 1 h 25 SR
Type B 2 h 4 h 15 SR
Availability 70 h 110 h
- How many units to produce from each product
type in order to maximize the profit?
2
A Toy Production Problem
Product Man-Power Machine Profit
Type A 3 h 1 h 25 SR
Type B 2 h 4 h 15 SR
Availability 70 h 110 h
- xA number of units of product type A
- xB number of units of product type B
- Total Profit 25 xA 15 xB
- Man-Power availability 3 xA 2 xB ? 70
- Machine availability xA 4 xB ? 110
3
A Toy Production Problem
- The corresponding linear program (LP) is
Objective function
Max Z 25 xA 15 xB Subject to 3 xA 2 xB ? 70 xA 4 xB ? 110 xA , xB ? IN
Constraints
Decision Variables
4
A Toy Production Problem
- The optimal solution of the LP is
- xA 22 , xB 2 and Z 580 SR
- The optimal solution of the toy production
problem is to produce 22 units of toy A and 2
units of toy B. - The optimal profit is 580 SR.
5
A Banking Problem
Type of loan Profit rate Bad debt ratio
1 Personal 0.14 0.10
2 Car 0.13 0.07
3 Home 0.12 0.03
4 Farm 0.125 0.05
5 Commercial 0.10 0.03
- A bank is in the process to allocate 12 million
SR to different types of loans. - Competition with other financial institutions
suggests allocating at least 40 of the funds to
farm commercial loans. - To assist in the housing industry, the home
loans must be at least 50 of the personal, car
and home loans. - The bank management requires that the overall
bad ratio debt not to exceed 4. - The bank wants to determine the best loan policy
that will maximize its profit rate.
6
A Banking Problem
Type of loan Profit rate Bad debt ratio
1 Personal 0.14 0.10
2 Car 0.13 0.07
3 Home 0.12 0.03
4 Farm 0.125 0.05
5 Commercial 0.10 0.03
Decision variables x1 amount of personal loans
(in million SR) x2 amount of car loans (in
million SR) x3 amount of home loans (in million
SR) x4 amount of farm loans (in million SR) x5
amount of commercial loans (in million SR)
7
A Banking Problem
Type of loan Profit rate Bad debt ratio
1 Personal 0.14 0.10
2 Car 0.13 0.07
3 Home 0.12 0.03
4 Farm 0.125 0.05
5 Commercial 0.10 0.02
Objective function Max Z 0.14(0.90)x1
0.13(0.93)x2 0.12(0.97)x30.125(0.95)x40.1
(0.98)x5 - 0.1x1- 0.07x2- 0.03x3- 0.05x4-0.02x5
8
A Banking Problem
Type of loan Profit rate Bad debt ratio
1 Personal 0.14 0.10
2 Car 0.13 0.07
3 Home 0.12 0.03
4 Farm 0.125 0.05
5 Commercial 0.10 0.03
- Constraints
- The total funds shall not exceed 12 million SR
- x1x2 x3 x4x5 ? 12
- Farm and commercial loan constraint
- x4x5 ? 0.4(x1x2 x3 x4x5)
- Home loans constraint
- x3 ? 0.5(x1x2 x3)
9
A Banking Problem
Type of loan Profit rate Bad debt ratio
1 Personal 0.14 0.10
2 Car 0.13 0.07
3 Home 0.12 0.03
4 Farm 0.125 0.05
5 Commercial 0.10 0.03
- Constraints
- Limit on bad debts rule
- (0.1x1 0.07x2 0.03x3 0.05x40.02x5)/( x1x2
x3 x4x5) ? 0.04 - (NONLINEAR)
- or equivalently,
- 0.06x1 0.03x2- 0.01x3
0.01x4- 0.02x5 ? 0
10
A Banking Problem
- The optimal solution of the LP is
- x1 x2 x4 0 , x3 7.2, x5 4.8 and
Z 0.99648 - The optimal solution consists in allocating 7.2
M to the home type and 4.8 M to commercial type. - The optimal profit is 0.996 M SR.
11
A Telecommunication Problem
- We have to place transmitters on the sites
A,B,,G. - Each transmitter covers the two adjacent zones
(e.g. if a transmitter is placed on site D, then
it will cover both zones 3 and 4). - Each Zone must be covered with at least one
transmitter. - Zone 4 must be covered by at least 2
transmitters. - What is the minimum number of transmitters to be
placed? - Where should they be placed?
12
A Telecommunication Problem
Decision variables xi 1 if a transmitter is to
be placed on site i (i A,B,,G) 0
otherwise Objective function Min Z xA xB
xC xD xE xF xG
13
A Telecommunication Problem
- Constraints
- xA xB xC ? 1 (Zone 1)
- xA xE xF ? 1 (Zone 2)
- xB xD ? 1 (Zone 3)
- xC xD xE xG ? 2 (Zone 4)
- xF xG ? 1 (Zone 5)
- xi ? 0,1 for all iA,B,,G
14
A Telecommunication Problem
- The optimal solution of the LP is
- xA xD xG 1
- xB xC xE xF 0
- Z 3
- The optimal solution of the telecommunication
problem is to place one transmitter at each of
the sites A, D, and G.
15
A Transportation Problem
Sources
Destinations
Demand 4 5 8
Supply 8 9
Unit transportation cost
- All the demands must be satisfied.
- All the supplies must be delivered.
- How many units to transport from each source to
each destination in order to minimize the total
transportation cost?
16
A Transportation Problem
Sources
Destinations
Demand 4 5 8
Supply 8 9
Unit transportation cost
- xij number of units transported from Source i
to Destination j - i1,2 jA,B,C
- Objective function
- Min Z 5 x1A 3 x1B 6 x1C 4 x2A 7 x2B
2 x2C
17
A Transportation Problem
Sources
Destinations
Demand 4 5 8
Supply 8 9
- Constraints
- x1A x1B x1C 8 (Supply of D1)
- x2A x2B x2C 9 (Supply of D2)
- x1A x2A 4 (Demand of
A) - x1B x2B 5 (Demand of
B) - x1C x2C 8 (Demand of
C) - x1A ,x1B , x1C , x2A , x2B , x2C ? IN
18
A Transportation Problem
Sources
Destinations
Demand 4 5 8
Supply 8 9
Optimal solution x1A 3, x1B 5, x1C 0,
x2A 1, x2B 0, x2C 8 Z 50