Token-passing Algorithms for mutual exclusion

1
Token-passing Algorithms for mutual exclusion

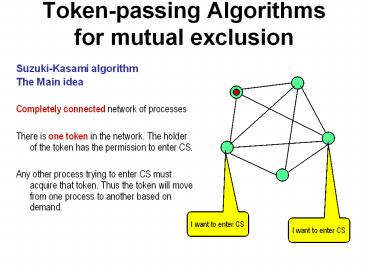
• Suzuki-Kasami algorithm
• The Main idea
• Completely connected network of processes
• There is one token in the network. The holder of
  the token has the permission to enter CS.
• Any other process trying to enter CS must acquire
  that token. Thus the token will move from one
  process to another based on demand.

I want to enter CS
I want to enter CS
2
Suzuki-Kasami Algorithm
req
last

• Process i broadcasts (i, num)
• Each process maintains
• -an array req reqj denotes the sequence no of
  the latest request from process j
• (Some requests will be stale soon)
• Additionally, the holder of the token maintains
• -an array last lastj denotes the sequence
  number of the latest visit to CS from for process
  j.
• - a queue Q of waiting processes

req
Sequence number of the request
queue Q
req
req
req
req array0..n-1 of integer
last array 0..n-1 of integer
3
Suzuki-Kasami Algorithm

• When a process i receives a request (k, num) from
• process k, it sets reqk to max(reqk, num).
• The holder of the token
• --Completes its CS
• --Sets lasti its own num
• --Updates Q by retaining each process k only if
• 1 lastk reqk
• (This guarantees the freshness of the request)
• --Sends the token to the head of Q, along with
• the array last and the tail of Q
• In fact, token ? (Q, last)

Req array0..n-1 of integer
Last Array 0..n-1 of integer
4
Suzuki-Kasamis algorithm

• Program of process j
• Initially, ?i reqi lasti 0
• Entry protocol
• reqj reqj 1
• Send (j, reqj) to all
• Wait until token (Q, last) arrives
• Critical Section
• Exit protocol
• lastj reqj
• ?k ? j k ? Q ? reqk lastk 1 ? append k
  to Q
• if Q is not empty ? send (tail-of-Q, last) to
  head-of-Q fi
• Upon receiving a request (k, num)
• reqk max(reqk, num)

5
Example
req1,0,0,0,0
req1,0,0,0,0 last0,0,0,0,0
1
0
2
req1,0,0,0,0
4
req1,0,0,0,0
3
req1,0,0,0,0
initial state process 0 has sent a request to
all, and grabbed the token
6
Example
req1,1,1,0,0
req1,1,1,0,0 last0,0,0,0,0
1
0
2
req1,1,1,0,0
4
req1,1,1,0,0
3
req1,1,1,0,0
1 2 send requests to enter CS
7
Example
req1,1,1,0,0
req1,1,1,0,0 last1,0,0,0,0 Q(1,2)
1
0
2
req1,1,1,0,0
4
req1,1,1,0,0
3
req1,1,1,0,0
0 prepares to exit CS
8
Example
req1,1,1,0,0 last1,0,0,0,0 Q(2)
req1,1,1,0,0
1
0
2
req1,1,1,0,0
4
req1,1,1,0,0
3
req1,1,1,0,0
0 passes token (Q and last) to 1
9
Example
req2,1,1,1,0 last1,0,0,0,0 Q(2,0,3)
req2,1,1,1,0
1
0
2
req2,1,1,1,0
4
req2,1,1,1,0
3
req2,1,1,1,0
0 and 3 send requests
10
Example
req2,1,1,1,0
req2,1,1,1,0
1
0
2
req2,1,1,1,0 last1,1,0,0,0 Q(0,3)
4
req2,1,1,1,0
3
req2,1,1,1,0
1 sends token to 2
11
Raymonds tree-based algorithm
1
4
1
4,7
1,4
1,4,7 want to enter their CS
12
Raymonds Algorithm
1
4
1,4
4,7
2 sends the token to 6
13
Raymonds Algorithm
4
4
These two directed edges will reverse their
direction
4
4,7
6 forwards the token to 1
The message complexity is O(diameter) of the
tree. Extensive empirical measurements show that
the average diameter of randomly chosen trees of
size n is O(log n). Therefore, the authors claim
that the average message complexity is O(log n)
14
Distributed Snapshot
15
Distributed snapshot

• -- How many messages are in transit
• on the internet?
• -- What is the global state of a distributed
  system of N processes?
• How do we compute these?

16
Think about these

• -- How many messages are in transit
• on the internet?
• -- What is the global state of a distributed
  system of N processes?
• How do we compute these?

17
One-dollar bank

Let a 1 coin circulate in a network of a million
banks. How can someone count the total in
circulation? If not counted properly, then one
may think the total in circulation to be one
million.
18
Importance of snapshots

• Major uses in
• - deadlock detection
• - termination detection
• - rollback recovery
• - global predicate computation

19
Consistent cut
A cut is a set of events.

• (a ? consistent cut C) ? (b happened before
  a) ? b ? C
• If this is not true, then the cut is inconsistent

b
g
c
time
a
d
P1
e
m
f
P2
P3
k
h
i
j
Cut 1
Cut 2
(Not consistent)
(Consistent)
20
Consistent snapshot

• The set of states immediately following the
  events (actions) in a consistent cut forms a
  consistent snapshot of a distributed system.
• A snapshot that is of practical interest is the
  most recent one. Let C1 and C2 be two consistent
  cuts and C1 ? C2. Then C2 is more recent than C1.
• Analyze why certain cuts in the one-dollar bank
  are inconsistent.

21
Consistent snapshot

• How to record a consistent snapshot? Note that
• 1. The recording must be non-invasive.
• 2. Recording must be done on-the-fly.
• You cannot stop the system.