Elements of Feedback Control

1
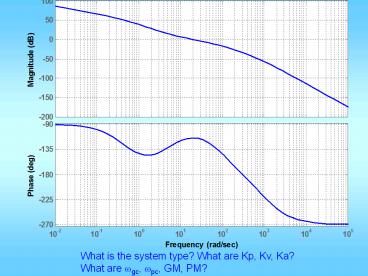
What is the system type? What are Kp, Kv,
Ka? What are wgc, wpc, GM, PM?
2
Stability from Nyquist plot
G(s)

• The completeNyquist plot
• Plot G(j?) for ? 0 to 8
• Get complex conjugate of plot, thats G(j?) for
  ? 0 to 8
• If G(s) has pole on j?-axis, treat separately
• Mark direction of ? increasing
• Locate point 1

3

• As you follow along the G(j?) curve for one
  complete cycle, you may encircle the 1 point
• Going around in c.w. once is 1 encirclement
• c.c.w. once is 1 encirclement

4
(No Transcript)
5

1. Nyquist criterion (unstable poles of
   closed-loop) Z (unstable poles of
   open-loop) P encirclement Nor Z P
   NTo have closed-loop stable need Z 0,
   i.e. N P

6

• That is G(j?) needs to encircle the 1 point
  c.c.w. P times.
• If open loop is stable to begin with, G(j?)
  cannot encircle the 1 point for closed-loop
  stability
• In previous example
• No encirclement, N 0.
• Open-loop stable, P 0
• Z P N 0, no unstable poles in
  closed-loop, stable

7
Example
4/(s-1)
8
As you move around from ? 8 to 0, to 0, to
8, you go around 1 c.c.w. once.
encirclement N 1. unstable pole P 1
9
i.e. unstable poles of closed-loop
0 closed-loop system is stable. Check c.l.
pole at s 3, stable.
10

• Example
• Get G(j?) for? 0 to 8
• Use conjugate to get G(j?) for? 8 to 0
• How to go from ? 0 to ? 0? At ? 0

11
Tiny radius
CCW
Huge radius
CW
Around a simple jw-axis pole, G(jw) sweeps CW 180
deg
Around a double pole on jw-axis, G(jw) sweeps CW
360 deg
12
(No Transcript)
13
encirclement N _____ open-loop unstable
poles P _____ Z P N ________
closed-loop unstable poles. closed-loop
stability _______
14

• Example
• Given
• G(s) is stable
• With K 1, performed open-loop sinusoidal tests,
  and G(j?) is on next page
• Q 1. Find stability margins
• 2. Use Nyquist criterion to determine
  closed-loop stability

G(s)
K
15
(No Transcript)
16

• Solution
• Where does G(j?) cross the unit circle?
  ________ Phase margin ________Where does
  G(j?) cross the negative real axis?
  ________ Gain margin ________Is closed-loop
  system stable withK 1? ________

17
Note that the total loop T.F. is KG(s). If K is
not 1, Nyquist plot of KG(s) is a scaling of
G(j?). e.g. If K 2, scale G(j?) by a factor of
2 in all directions. Q How much can K increase
before GM becomes lost? ________ How much can K
decrease? ______
18
Some people say the gain margin is 0 to 5 in
this example Q As K is increased from 1 to 5,
GM is lost, what happens to PM? Whats the max
PM as K is reduced to 0 and GM becomes 8?
19

• To use Nyquist criterion, need complete Nyquist
  plot.
• Get complex conjugate
• Connect ? 0 to ? 0 through an infinite
  circle
• Count encirclement N
• Apply Z P N
• o.l. stable, P _______
• Z _______
• c.l. stability _______

20
(No Transcript)
21
G(s)

• Example
• G(s) stable, P 0
• G(j?) for ? gt 0 as given.
• Get G(j?) for? lt 0 by conjugate
• Connect ? 0 to ? 0.But how?

22
Choice a) Wheres 1 ? encirclement N
_______ Z P N _______ Make sense? _______
23
Choice b) Where is1 ? encir.N _____ Z
P N _______ closed-loopstability _______
24
Note If G(j?) is along Re axis to 8 as ??0,
it means G(s) has in it. when s makes a half
circle near ? 0, G(s) makes a full circle near
8. choice a) is impossible,but choice b) is
possible.
25
(No Transcript)
26

• Example G(s) stable, P 0
• Get conjugatefor ? lt 0
• Connect ? 0to ? 0.Needs to goone full
  circlewith radius 8.Two choices.

27
Choice a) N 0 Z P N
0 closed-loopstable
28
Choice b) N 2 Z P N 2 Closedloop has
two unstable poles
29
Which way is correct? For stable non-minimum
phase systems,
30

• Example G(s) has one unstable pole
• P 1, no unstable zeros
• Get conjugate
• Connect? 0to ? 0.How?One
  unstablepole/zeroIf connect in c.c.w.

31
encirclement N ? If 1 is to the left of
A i.e. A gt 1 then N 0 Z P N 1 0
1 but if a gain is increased, 1 could be
inside, N 2 Z P N 1 c.c.w. is
impossible
32
If connect c.w. For A gt 1N ______ Z P
N ______ For A lt 1N ______ Z ______ No
contradiction. This is correct way.
33
Example G(s) stable, minimum phase P
0 G(j?) as given get conjugate. Connect ?
0 to ? 0,
34
If A lt 1 lt 0 N ______ Z P N
______ stability of c.l. ______ If B lt 1 lt
A N ______ Z P N ______ closed-loo
p stability ______
35
If C lt 1 lt B N ______ Z P N
______ closed-loop stability ______ If 1 lt C
N ______ Z P N ______ closed-loop
stability ______
36
function mynyquist(n,d,w) mynyquist-- plots a
nonlinearly compressed nyquist plot. Near the
origin (distance less than 2), it preserves the
original Nyquist plot. Far away from the origin
(distance more than 2), the distance is
compressed by taking the log. Syntax
mynyquist(n,d), or mynyquist(n,d,w) where n
and d are the numerator and denominator of the
transfer function, w is the desired frequency
points. The program does not handle jw-axis
poles. if nargin lt3 m,p,wbode(n,d)
d1log10(min(w)) d2log10(max(w))
wlogspace(d1, d2, 200) end
37
Gpolyval(n, jw)./polyval(d,jw) or
Gevalfr(tf(n,d),jw) GAabs(G) GPangle(G) GA
A(GAlt2).GA(GAgt2).(22log(GA/2)) if GAlt2,
do nothing ifgt2, do log compression plot(GAA.co
s(GP),GAA.sin(GP),'b') hold plot(GAA.cos(GP),-
GAA.sin(GP),'r') this plots the negative freq
part axis equal axis(-3 1 -2 2) this
sets x, y limits for the graph window grid a02
pi/2002pi plot(cos(a),sin(a),'') this
plots the unit circle for phase margin hold
38
nyquist(23conv(1 .25,1 0.7 1),conv(0.15
1,conv(1 10 0 0,1 0.5 0.25)))
39
mynyquist(23conv(1 .25,1 0.7 1),conv(0.15
1,conv(1 10 0 0,1 0.5 0.25)))
40
(No Transcript)
41
(No Transcript)
42
(No Transcript)
43
(No Transcript)
44
For small zeta, resonance freq is about wn BW
ranges from 0.5wn to 1.5wn For good z range, BW
is 0.8 to 1.1 wn So take BW wn
z0.1
0.2
0.3
No resonance for z lt 0.7 Mr1dB for
z0.6 Mr3dB for z0.5 Mr7dB for z0.4
45
(No Transcript)
46
0.2
z0.1
0.3
0.4
wgc
In the range of good zeta, wgc is about 0.65
times to 0.8 times wn
w/wn
47
(No Transcript)
48
In the range of good zeta, PM is about 100z
z0.1
0.2
0.3
0.4
w/wn
49
(No Transcript)