Eye Physiology

1
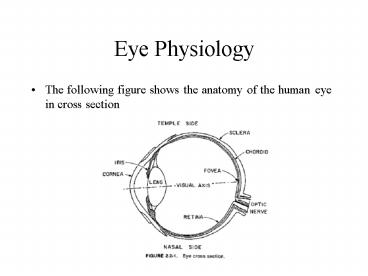
Eye Physiology

• The following figure shows the anatomy of the
  human eye in cross section

2
Eye Physiology

• There are two types of receptors in the retina
• The rods are long slender receptors
• The cones are generally shorter and thicker in
  structure
• The rods and cones are not distributed evenly
  around the retina.
• Rods and cones operate differently
• Rods are more sensitive to light than cones.
• At low levels of illumination the rods provide a
  visual response called scotopic vision
• Cones respond to higher levels of illumination
  their response is called photopic vision

3
(No Transcript)
4
(No Transcript)
5
Eye Physiology

• Rods are more sensitive to light than the cones.

6
Eye Physiology

• The eye contains about 6.5 million cones and 100
  million rods distributed over the retina.
• The density of the cones is greatest at the
  fovea, this is the region of sharpest photopic
  vision.

7
Eye Physiology

• There are three basic types of cones in the
  retina
• These cones have different absorption
  characteristics as a function of wavelength with
  peak absorptions in the red, green, and blue
  regions of the optical spectrum.

• is blue, b is green, and g is red
• There is a relatively low sensitivity to blue
  light
• There is a lot of overlap

8
Eye Physiology

• The optic nerve bundle contains on the order of
  800,000 nerve fibers.
• There are over 100,000,000 receptors in the
  retina.
• Therefore, the rods and cones must be
  interconnected to nerve fibers on a many-to-one
  basis.

9
Contrast Sensitivity
0
1
2
3
4
Circle constant
Background constant
Just noticeable difference (JND) at 2
10
Contrast Sensitivity
0
1
2
3
4
Circle constant
Background constant
Just noticeable difference (JND) at 2
11
Contrast Sensitivity
0
1
2
3
4
Backgrounddifferent thenboth halves
Backgroundsame asright half
Just noticeable difference (JND) 4 (top) and
2 (bottom)
12
Contrast Sensitivity
0
1
2
3
4
Backgrounddifferent thenboth halves
Backgroundsame asright half
Just noticeable difference (JND) 4 (top) and
2 (bottom)
13
Contrast Sensitivity

• The response of the eye to changes in the
  intensity of illumination is nonlinear
• Consider a patch of light of intensity idI
  surrounded by a background intensity I as shown
  in the following figure

14
Contrast Sensitivity

• Over a wide range of intensities, it is found
  that the ratio dI/I, called the Weber fraction,
  is nearly constant at a value of about 0.02.
• This does not hold at very low or very high
  intensities
• Furthermore, contrast sensitivity is dependent on
  the intensity of the surround. Consider the
  second panel of the previous figure.

15
Logarithmic Response of Cones and Rods

• The response of the cones and rods to light is
  nonlinear. In fact many image processing systems
  assume that the eye's response is logarithmic
  instead of linear with respect to intensity.
• To test the hypothesis that the response of the
  cones and rods are logarithmic, we examine the
  following two cases
• If the intensity response of the receptors to
  intensity is linear, then the derivative of the
  response with respect to intensity should be a
  constant. This is not the case as seen in the
  next figure.

16
(No Transcript)
17
Logarithmic Response of Cones and Rods

• To show that the response to intensity is
  logarithmic, we take the logarithm of the
  intensity response and then take the derivative
  with respect to intensity. This derivative is
  nearly a constant proving that intensity response
  of cones and rods can be modeled as a logarithmic
  response.
• Another way to see this is the following, note
  that the differential of the logarithm of
  intensity is d(log(I)) dI/I. Figure 2.3-1
  shows the plot of dI/I for the intensity response
  of the human visual system.
• Since this plot is nearly constant in the middle
  frequencies, we again conclude that the intensity
  response of cones and rods can be modeled as a
  logarithmic response.

18
Simultaneous Contrast

• The simultaneous contrast phenomenon is
  illustrated below.
• The small squares in each image are the same
  intensity.
• Because the different background intensities, the
  small squares do not appear equally bright.

19
Simultaneous Contrast

• Perceiving the two squares on different
  backgrounds as different, even though they are in
  fact identical, is called the simultaneous
  contrast effect.
• Psychophysically, we say this effect is caused by
  the difference in the backgrounds, but what is
  the physiological mechanism behind this effect?

20
Simultaneous Contrast

• Perceiving the two squares on different
  backgrounds as different, even though they are in
  fact identical, is called the simultaneous
  contrast effect.
• Psychophysically, we say this effect is caused by
  the difference in the backgrounds, but what is
  the physiological mechanism behind this effect?

Lateral Inhibition
21
Lateral Inhibition

• Record signal from nerve fiber of receptor A.
• Illumination of receptor A alone causes a large
  response.
• Add illumination to three nearby receptors at B
  causes the response at A to decrease.
• Increasing the illumination of B further
  decreases As response.
• Thus, illumination of the neighboring receptors
  inhibited the firing of receptor A.
• This inhibition is called lateral inhibition
  because it is transmitted laterally, across the
  retina, in a structure called the lateral plexus.

22
Lateral Inhibition
23
Lateral Inhibition

• A neural signal is assumed to be generated by a
  weighted contribution of many spatially adjacent
  rods and cones.
• Some receptors exert an inhibitory influence on
  the neural response.
• The weighting values are, in effect, the impulse
  response of the human visual system beyond the
  retina.

24
Lateral Inhibition
25
Mach Band Effect

• Another effect that can be explained by the
  lateral inhibition.
• The Mach band effect is illustrated in the figure
  below.
• The intensity is uniform over the width of each
  bar.
• However, the visual appearance is that each strip
  is darker at its right side than its left.

26
Mach Band

• The Mach band effect is illustrated in the figure
  below.
• A bright bar appears at position B and a dark bar
  appears at D.

27
Modulation Transfer Function (MTF) experiment

• An observer is shown two sine wave grating
  transparencies, a reference grating of constant
  contrast and spatial frequency, and a
  variable-contrast test grating whose spatial
  frequency is set at some value different from
  that of the reference.
• Contrast is defined as the ratio (max-min)/(max
  min)where max and min are the maximum and
  minimum of the grating intensity, respectively.
• The contrast of the test grating is varied until
  the brightness of the bright and dark regions of
  the two transparencies appear identical.

28
Modulation Transfer Function (MTF) experiment

• In this manner it is possible to develop a plot
  of the MTF of the human visual system.
• Note that the response is nearly linear for an
  exponential sine wave grating.

29

• Note that the envelope of the visible bars
  generally follows the MTF curves of the previous
  figure.

30
Logarithmic model for monochrome vision

• It has been postulated that the nonlinear
  response of the eye to intensity variations is
  logarithmic in nature and occurs near the
  beginning of the visual information processing
  system.
• Below is a simple logarithmic eye model for
  monochromatic vision.

31
Monochrome Vision Model

• The logarithmic/linear system eye model provides
  a reasonable prediction of visual response over a
  wide range of intensities.
• However, at high spatial frequencies and at very
  low or very high intensities, observed responses
  depart from responses predicted by the model.

32
Lateral Inhibition
33
Extended model for Monochrome Vision
34
Subjective Color

• Intermittent pulses of white light are perceived
  as colored light.
• 1894 Benham invented the following experiment.
• Spinning the disk CCW
• Outer ring appears red
• Middle ring appears green
• Inner ring appears blue
• CW rotation reverses thecolors of the inner and
  outer rings.
• This effect is due to the temporal response of
  the human visual system to flashing lights.

35
Chromatic Adaption

• The hue of a perceived color is dependent on the
  adaption of a viewer.
• For example, the American flag will not
  immediately appear red, white, and blue if the
  viewer has been subjected to high-intensity red
  light before viewing the flag.
• The colors of the flag will appear to shift in
  hue toward the red complement, cyan.

36
(No Transcript)
37
Color Blindness

• Approximately 8 of males and 1 of females are
  subject to some form of color blindness.
• Monochromats only possess rods or rods plus one
  type of cone.
• Dichromats possess two of the three types of
  cones.
• Both monochromats and dichromats can distinguish
  colors insofar as they have learned to associate
  particular colors with particular objects.

38
Classroom Experiments

• Use Matlab to reproduce the Weber Fraction plot.
• Use Matlab to reproduce the Mach band effect with
  uniform intensity bars (figure 2.3-2).
• Use Matlab to reproduce the Mach band effect with
  the sigmoid intensity profile (figure 2.3-2).
• Use Matlab to reproduce the simultaneous contrast
  phenomenon (figure 2.3-3).
• Use Matlab to display a simple American flag and
  a solid red square to reproduce the chromatic
  adaption experiment from Pratt.

39
Color Vision Model

• Trichromatic Model of human color vision
• The eye possesses 3 types of sensors, each
  sensitive over a different wavelength band
• Receptor spectral sensitivities s1(l), s2(l), and
  s3(l) represent the absorption pigments of the
  retina.
• Receptors produce signalswhere C(l) is the
  spectral energy distribution of the incident
  light source.

40
Color Vision Model

• Spectral Sensitivities si(l) in Fig 2.2-4 where
  obtained by spectral absorption measurements of
  cone pigments.
• Direct physiological measurements are difficult
  to perform accurately.
• Indirect estimates of cone spectral sensitivities
  have been obtained from measurements of the color
  response of color blind individuals Konig and
  Brodhun.

41
Color Vision Model

• The 3 signals e1, e2, e3 are subject to a
  logarithmic transfer function and combined to
  produce the outputs.

42
Color Vision Model

• Finally, the signals d1, d2, d3 pass through
  linear systems with transfer functions H1, H2,
  and H3, to produce the output signals g1, g2, g3
  that provide the basis for perception of color by
  the brain.

43
Color Vision Model

• d2 and d3 are related to the chromaticity of a
  colored light.
• d1 is proportional to luminance.
• This model satisfies the basic laws of
  colorimetry.
• If the spectral energy of a colored light changes
  by a constant multiplicative factor, the hue and
  saturation of light, as described by its
  chromaticity coordinates, remains invariant over
  a wide dynamic range, i.e., d2 and d3 do not
  change.
• The luminance d1 increases in a logarithmic
  manner.

44
Color Vision Model

• Just like the monochrome model, the logarithmic
  color vision model may be extend to a more
  accurate model.
• The linear transfer functions HE1, HE2, HE3,
  account for the optical response of the eye
• A point non-linearity is substituted for the
  logarithmic transfer function.

45
Color Vision Model

• Sine wave response measurements for colored
  lights were performed by van der Horst, de Weert,
  and Bouman.
• Chromatic response is shifted toward low spatial
  frequencies relative to the luminance response.

46
Gamma Correction

• Red, green, and blue signals from video camera
  sensors typically are linearly proportional to
  the light striking each sensor.
• However, light generated by CRT displays is
  approximately equal to the display amplitude
  drive signals raised to a power in the range of
  2.0 to 3.0.
• Gamma correction is a compensation process that
  corrects for this nonlinear difference.
• The camera sensor signal is passed through a
  nonlinear system with a power, typically, of
  about 0.45.

47
Gamma Correction

• In a video system, luminance of each of the
  linear-light red, green, and blue (tristimulus)
  components is transformed to a nonlinear video
  signal by gamma correction, which is universally
  done at the camera.
• The Rec. 709 transfer function takes linear-light
  tristimulus value (here L) to a nonlinear
  component (here E'), for example, voltage in a
  video system

48
Gamma Correction

• The linear segment near black minimizes the
  effect of sensor noise in practical cameras and
  scanners. Here is a graph of the Rec. 709
  transfer function, for a signal range from zero
  to unity

49
Gamma Correction

• An idealized monitor inverts the transform
• Real monitors are not as exact as this equation
  suggests, and have no linear segment, but the
  precise definition is necessary for accurate
  intermediate processing in the linear-light
  domain.
• In a color system, an identical transfer function
  is applied to each of the three tristimulus
  (linear-light) RGB components.

50
Gamma Correction

• The nonlinearity of a CRT is a function of the
  electrostatics of the cathode and the grid of an
  electron gun it has nothing to do with the
  phosphor.
• The nonlinearity is a power function f (x)
  xa, not an exponential function f (x) ex.

51
Gamma Correction

• To reduce TV receiver cost, gamma correction is
  performed at the television camera rather than
  the receiver.
• A linear RGB image that has been gamma corrected
  is called a gamma RGB image.
• LCD displays are reasonably linear in the sense
  that the light generated is approximately
  proportional to the display amplitude drive
  signal.
• LCDs usually employ circuitry to compensate for
  the gamma correction at the sensor.

52
Gamma Correction

• In video, a 0.45-power function is applied at the
  camera
• Synthetic computer graphics calculates the
  interaction of light and objects. These
  interactions are in the physical domain, and must
  be calculated in linear-light values. It is
  conventional in computer graphics to store
  linear-light values in the frame buffer, and
  introduce gamma correction at the lookup table at
  the output of the frame buffer.

53
Gamma Correction

• If linear-light is represented in just eight
  bits, near black the steps between codes will be
  perceptible as banding in smoothly-shaded images.
  This is the eight-bit bottleneck in the sketch.
• Desktop computers are optimized neither for image
  synthesis nor for video. They have programmable
  "gamma" and either poor standards or no
  standards. Consequently, image interchange among
  desktop computers is fraught with difficulty.

54
References

• J.S. Lim, Two-Dimensional Signal and Image
  Processing, Prentice Hall, 1991.
• W.K. Pratt, Digital Image Processing, Wiley
  Interscience, 3rd ed., 2001.
• Charles Poynton's Frequently Asked Questions
  about Colorhttp//www.inforamp.net/poynton/Color
  FAQ.html
• Charles Poynton's Frequently Asked Questions
  about Gamma.http//www.inforamp.net/poynton/Gamm
  aFAQ.html

55
(No Transcript)
56
Psychophysical Vision Properties

• Let E(l) represent the spectral energy
  distribution of light emitted from some primary
  light source.
• Let t(l) and r(l) denote the wavelength dependent
  transmissivity and reflectivity, respectively, of
  an object
• For a transmissive object, the observed light
  spectral energy distribution is
• C(l) t(l)E(l)
• and for a reflective object
• C(l) r(l)E(l).

57
Photometry

• The Commission Internationale de lEclairage
  (C.I.E.) sets the standards for light and color.
• SA is a tungsten filament lamp
• SB approximates direct sunlight
• SC approximates light from an overcast sky.
• A hypothetical source, called illuminant E, is
  assumed to emit constant radiant energy at all
  wavelengths.

58
Color Matching Quiz

• Is this Additive or Subtractive Color Matching?

59
Color Matching Quiz

• Is this Additive or Subtractive Color Matching?

60
Color Matching Quiz

• Is this Additive or Subtractive Color Matching?

61
Color Matching

• Additive Color Matching

Subtractive Color Matching
cyan
red
magenta
green
blue
yellow
62
Subtractive Color Matching

• The dye concentrations of the three spectral
  filters are varied until a perceptual match is
  obtained with a reference white W.
• The dye concentrations are recorded as A1 (W), A2
  (W), A3(W).

63
Subtractive Color Matching

• Next, the dye concentrations of the three
  spectral filters are varied until a perceptual
  match is obtained for the colored light C.
• If a match is possible, record the intensities
  asA1 (C), A2 (C), A3(C).
• The tristimulus values are computed as

64
Subtractive Color Matching

• One primary P3 is superimposed with the light
  C and compared to the overlap of the other two
  primaries P1 and P2.
• All primaries are adjusted until there is a
  match.
• If a match is possible, the tristimulus values
  are computed as

65
Subtractive Color Matching

• Two primaries P2 and P3 are superimposed with
  the light C and compared to the other primary
  P1.
• All primaries are adjusted until there is a
  match.
• If a match is possible, the tristimulus values
  are computed as