Table 16 Truth tables of logical operations

1
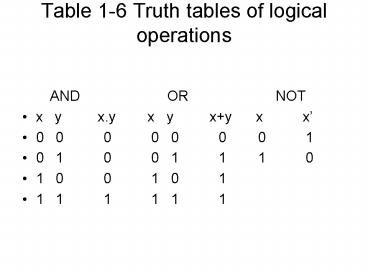
Table 1-6 Truth tables of logical operations

• AND OR
  NOT
• x y x.y x y xy x
  x
• 0 0 0 0 0 0
  0 1
• 0 1 0 0 1 1
  1 0
• 1 0 0 1 0 1
• 1 1 1 1 1 1

2

• For the switches in parallel, the light turns on
  if A or B are closed. It is obvious that the two
  circuit expressed by means binary logic with the
  AND and OR operations, respectively
• LA.B for the circuit of Fig 1-4
• LAB for the circuit of Fig 1-4

3
Switching Circuits and Binary Signals

• The use of binary variables and the application
  of binary logic are demonstrated by the simple
  switching circuits of Fig 1-4.
• Let manual switches A and B represent two binary
  variables with values equal to 0 when the switch
  is open and 1 when the switch is closed.
• Similarly, the lamp L represent a third binary
  variable equals 1 when the light on and 0 when
  off.
• For the switches in series, the light turns on if
  A and B are closed.

4

• Electronic digital circuits are sometimes called
  Switching circuits because they behave like a
  switch, with the active element such as a
  transistor either conducting (Switch closed) or
  not conducting (switch open).
• Instead of changing manually, an electronic
  switching circuit uses binary signal to control
  the conduction or non conduction state of the
  active element.
• Electrical signals such as voltages or currents
  exit through out a digital system in either one
  or two recognizable values (except during
  transition).
• Voltage operated circuits, for example respond to
  two separate voltage levels which represent a
  binary variable equal to logic-1 or logic-0.
• For example, a particular digital system may
  define logic logic-1 as a signal with a nominal
  value of 3 volts and logic-0 as a signal of
  nominal value of 0 volts.

5
Logic Gates

• Electronic digital circuits are also called logic
  circuits because, with the proper input, they
  established logical manipulation paths.
• Any desired information for computing or control
  can be operated upon by passing binary signals
  through various combinations of logic circuits,
  such signal representing a value and carrying one
  bit of information.
• Logic circuits that perform the logical
  operations of AND, OR, and NOT are shown in their
  symbols in Fig1-6.
• These circuits, called Gates, are blocks of
  hardware that produce a logic-1 or logic-0 output
  signal if input logic requirements are satisfied.
  
• Note that four different names have been used for
  the same type of circuits digital circuits,
  switching circuits, logic circuits, and gates.
• The NOT gate is sometimes called an inverter
  circuit since it inverts a binary signal.
• The input signals x and y in the two-input gates
  of Fig 1-6 may exist in one of four possible
  states 00, 10, 11, or 01.
• These input signals are Fig. 1-7, together with
  the output signals for the AND and OR gates.

6
Integrated Circuits

• Digital circuits are invariably constructed with
  integrated circuits. Integrated circuits
  (abbreviated IC) are a small silicon
  semiconductor crystal, called a chip, containing
  electrical components such as transistors,
  diodes, resistors, and capacitors.
• The various components are interconnected inside
  the chip to form an electronic circuit.
• Integrated circuits are classified in two
  general categories, linear and digital.
• Linear ICs operate with continuous signals to
  provide electronic functions such as amplifiers
  and voltages comparators. Digital integrated
  circuits operate with binary signals and are made
  up of interconnected digital gates.
• As the technology of ICs has improved, the number
  of gates that can be put on a single silicon chip
  has increased considerably.
• Several logic gates in a single package make it a
  small-scale integration (SSI) device.
• To quality as a medium-scale integration (MSI)
  device, the IC must perform a complete logic
  function and have a complexity of 10 to 100
  gates.
• A large-scale integration (LSI) device performs a
  logic function with more than 100 gates. There
  are also very-large-scale integration (VLSI)
  devices that contain thousands of gates in a
  single chip.

7
IC DIGITAL LOGIC FAMILIES

• TTL Transistor-transistor logic
• ECL Emitter-coupled logic
• MOS Metal-oxide semiconductor
• CMOS Complementary metal-oxide semiconductor
• I2L Intergrated-injection logic
• TTL has an extensive list of digital functions
  and is currently the most popular logic family.
• ECL is used in systems requiring high-speed
  operations.
• MOS and I2L are used in circuits requiring high
  component density,
• CMOS is used in systems requiring low power
  consumption.

8
BOOLEAN ALGEBRA AND LOGIC GATES

• The postulates of a mathematical system form the
  basic assumptions from which it is possible to
  deduce the rules, theorems, and properties of the
  system. The most common postulates used to
  formulate various algebraic structures are
• Closure. A set of S is closed with respect to a
  binary operator if, for every pair of elements of
  S, the binary operator specifies a rule for
  obtaining a unique element of S. For example, the
  set of natural numbers N1,2,3,4, is closed
  with respect to the binary operator plus () by
  the rules of arithmetic addition, since for any
  a, bwe obtain a unique closed with respect to the
  binary by the operation a bc. The set of
  natural numbers is not closed with respect to the
  binary operator minus (-) by the rules of
  arithmetic subtraction because 2-3-1 and
  2,3,while (-1).

9

• Associative law A binary operator on a set S
  is said to be associative whenever
• for all x, y, z
• Commutative law A binary operator on a set S
  is said to be commutative whenever
• for all x, y
• Identity element A set S is said to have an
  identity element with respect to a binary
  operation on S if there exists an element ewith
  the property
• for every x Example The
  element 0 is an identity element with respect to
  operation on the set of integers
  I,-3,-2,-1,0,1,2,3,..Since
• For any xThe set of natural numbers N has no
  identity element since 0 is excluded from the
  set.
• Inverse A set S having the identity element e
  with respect to a binary operator is said to
  have an inverse whenever, for every there exists
  an element such that
• example In the set of integers
  I with e0, the inverse of an element a is (-a)
  since a(-a)0.
• Distributive law and are two binary operators
  on a set S, is said to be distributive over
  whenever

10

• Theorem 1(a) .
• xx(xx).1
  by postulate 2(b)
• (xx)(xx)
  5(a)
• xxx
  4(b)
• x0
  
  5(b)
• x
  
  2(a)
• Theorem 1(b) x.xx.
• x.xxx0
  by postulate 2(a)
• xxxx
  5(b)
• x(xx)
  4(a)
• x.1
  5(a)
• x
  2(b)
• Note that theorem 1(b) is the dual of theorem
  1(a) and that each step of the proof in part (b)
  is the dual of part (a). Any dual theorem can be
  similarly derived from the proof of its
  corresponding pair.
• Theorem 2(a) x11
• x11.(x1)
  by postulate 2(b)
• (xx)(x1)
  5(a)
• xx.1
  4(b)
• xx
  2(b)
• 1
  5(a)

11

• Theorem 2(b) x.00 by duality.
• Theorem 3 (x)x. From postulate 5, we have
  xx1 and x.x0, which defines the complement
  of x. The complement of x is x and is also
  (x). Therefore, since the complement is unique,
  we have that (x). Therefore, since the
  complement is unique, we have that (x)x.
• The theorems involving two or three variables may
  be proven algebraically from the postulates and
  the theorems which have already been proven.
  Take, for example, the absorption theorem
• Theorem 6(a) xxyx.
• xxyx.1 xy
  by postulate 2(b)
• x(1y)
  by postulate 4(a)
• x(y1)
  by postulate 3(a)
• x.1
  by theorem 2(a)
• x
  by postulate 2(b)

12

• Theorem 6(b) x(xy)x by duality
• The theorems of Boolean algebra can be shown to
  hold true by means of truth tables. In truth
  tables, both sides of the relation are checked to
  yield identical results for all possible
  combinations of variables involved. The following
  truth table verifies the first absorption
  theorem.
• x y xy
  xxy
• 0 0 0
  0
• 0 1 0
  0
• 1 0 0
  1
• 1 1 1
  1

13

• The algebraic proofs of the associative law and
  De Morgans theorem are long and will not be
  shown here. However, their validity is easily
  shown with truth tables. For example, the truth
  table for the first De Morgans theorem
  (xy)xy is shown below.
• x y xy (xy) x
  y xy
• 0 0 0 1 1
  1 1
• 0 1 1 0 1
  0 0
• 1 0 1 0 0
  1 0
• 1 1 1 0 0
  0 0

14

• So far we can see that applying Boolean algebra
  can be awkward in order to simplify expressions.
• Apart from being laborious (and requiring the
  remembering all the laws) the method can lead to
  solutions which, though they appear minimal, are
  not.
• The Karnaugh map provides a simple and
  straight-forward method of minimising boolean
  expressions.
• With the Karnaugh map Boolean expressions having
  up to four and even six variables can be
  simplified.

15
So what is a Karnaugh map?

• A Karnaugh map provides a pictorial method of
  grouping together expressions with common factors
  and therefore eliminating unwanted variables.
• The Karnaugh map can also be described as a
  special arrangement of a truth table.
• The diagram below illustrates the correspondence
  between the Karnaugh map and the truth table for
  the general case of a two variable problem.

16
The values inside the squares are copied from the
output column of the truth table, therefore there
is one square in the map for every row in the
truth table. Around the edge of the Karnaugh
map are the values of the two input variable. A
is along the top and B is down the left hand
side. The diagram below explains this
17
The values around the edge of the map can be
thought of as coordinates. So as an example,
the square on the top right hand corner of the
map in the above diagram has coordinates A1 and
B0. This square corresponds to the row in the
truth table where A1 and B0 and F1. Note
that the value in the F column represents a
particular function to which the Karnaugh map
corresponds.
18

• Example 1
• Consider the following map. The function plotted
  is Z f(A,B) A AB
• Note that values of the input variables form the
  rows and columns. That is the logic values of the
  variables A and B (with one denoting true form
  and zero denoting false form) form the head of
  the rows and columns respectively.
• Bear in mind that the above map is a one
  dimensional type which can be used to simplify an
  expression in two variables.
• There is a two-dimensional map that can be used
  for up to four variables, and a three-dimensional
  map for up to six variables.

19

• Using algebraic simplification,
• Z A AB
• Z A( B)
• Z A
• Variable B becomes redundant due to Boolean
  Theorem T9a.
• Referring to the map above, the two adjacent 1's
  are grouped together. Through inspection it can
  be seen that variable B has its true and false
  form within the group. This eliminates variable B
  leaving only variable A which only has its true
  form. The minimised answer therefore is Z A.

20

• Example 2
• Consider the expression Z f(A,B) A B
  plotted on the Karnaugh map

Pairs of 1's are grouped as shown above, and the
simplified answer is obtained by using the
following steps Note that two groups can be
formed for the example given above, bearing in
mind that the largest rectangular clusters that
can be made consist of two 1s. Notice that a 1
can belong to more than one group. The first
group labelled I, consists of two 1s which
correspond to A 0, B 0 and A 1, B 0. Put
in another way, all squares in this example that
correspond to the area of the map where B 0
contains 1s, independent of the value of A. So
when B 0 the output is 1. The expression of the
output will contain the term
21

• For group labelled II corresponds to the area of
  the map where A 0.
• The group can therefore be defined as . This
  implies that when A 0 the output is 1.
• The output is therefore 1 whenever B 0 and A
  0
• Hence the simplified answer is Z Verify this
  algebraically in your notebooks.

22
Problems

• Minimise the following problems using the
  Karnaugh maps method.
• Z f(A,B,C) B AB AC
• Z f(A,B,C) B B BC A

23

• By using the rules of simplification and ringing
  of adjacent cells in order to make as many
  variables redundant, the minimised result
  obtained is B AC

24

• Z f(A,B,C) B B BC A
• By using the rules of simplification and ringing
  of adjacent cells in order to make as many
  variables redundant, the minimised result
  obtained is B A

25
Karnaugh Maps - Rules of Simplification

• The Karnaugh map uses the following rules for the
  simplification of expressions by grouping
  together adjacent cells containing ones
• Groups may not include any cell containing a zero

26
Groups may be horizontal or vertical, but not
diagonal.

• Groups must contain 1, 2, 4, 8, or in general 2n
  cells. That is if n 1, a group will contain
  two 1's since 21 2.

27
If n 2, a group will contain four 1's since 22
4.
28
Each group should be as large as possible.
29
Each cell containing a one must be in at least
one group.
30
Groups may overlap.
31

• Groups may wrap around the table. The leftmost
  cell in a row may be grouped with the rightmost
  cell and the top cell in a column may be grouped
  with the bottom cell.

32

• There should be as few groups as possible, as
  long as this does not contradict any of the
  previous rules.

33
Summmary

• No zeros allowed.
• No diagonals.
• Only power of 2 number of cells in each group.
• Groups should be as large as possible.
• Every one must be in at least one group.
• Overlapping allowed.
• Wrap around allowed.
• Fewest number of groups possible.

34
The Tabular Method