Ejemplo de cifrado monoalfabtico

1
Ejemplo de cifrado monoalfabético
http//serdis.dis.ulpgc.es/7Eii-cript/PAGINA20WE
B20CLASICA/CRIPTOGRAFIA/MONOALFABETICAS/codigo20
de20cesar.htm
2
Inconvenientes del cifrado monoalfabético
La debilidad de los cifrados monoalfabéticos está
en que la frecuencia de aparición de cada letra
en el texto claro se refleja exactamente en el
criptograma. La misma frecuencia que tiene por
ejemplo la letra A en un texto en claro tendría
la letra asociada en el texto cifrado. Esto
representa muchas pistas para un posible
criptoanalista, sólo tiene que basarse en el
estudio de frecuencias y pensar un poco en
castellano
3
Inconvenientes del cifrado monoalfabético
la e es la letra mas frecuente

• l (3)
• a (4)
• (6)
• (2)
• (2)
• (2)
• (1)
• f (1)
• c (1)
• u (1)
• n (1)

Podemos pensar que e (aparece 6 veces ) es la e
la e es la letra mas frecuente
Podemos pensar que a (a parece 4 veces ) es la a
la e es la letra mas frecuente
Podemos pensar que l es la l, porque la primera
palabra
la e es la letra mas frecuente
Podemos pensar que s es la s, por la tercera
palabra
Ver frecuencias
la e es la letra mas frecuente
Actividad 5
4
Inconvenientes del cifrado monoalfabético
Ver frecuencias
la e es la letra mas frecuente
la e es la letra mas frecuente
Podemos pensar que t es la t, y la r es la r,
por la quinta palabra
la e es la letra mas frecuente
. . - .
la e es la letra mas frecuente
5
Inconvenientes del cifrado monoalfabético
Ver frecuencias
Aunque en mensajes cortos no siempre es tan fácil
???? ??? ?? ????
Podemos pensar que ? (aparece 4 veces ) es la e
?e?e ?e? ?? ???e
Podemos pensar que ?(aparece 2 veces ) es la a
ae?e ?e? a? ???e
y ahora qué hacemos?
6
Inconvenientes del cifrado monoalfabético.
Curiosidad

• El secuestro es un libro escrito por un francés
  llamado Georges Perec
• Este era un autor muy original que se dedicó a
  experimentar con el lenguaje y tiene algunos
  palíndromos increíbles
• En todo el libro no parece ni una e (tiene
  unas trescientas páginas)
• Pero los traductores al castellano, consiguen que
  en el libro no exista la a
• Traducción Marisol Arbués, Mercé Burrel, Marc
  Parayre,
• Hermes Slaceda, y Regina Vega. Editorial
  Anagrama. 1997
• Menuda forma de estropear el criptoanálisis!

O rey, o joyero Amad a la dama Somos o no somos.
7
Anécdota

• Más de 1500 años después, un cifrado similar al
  de César fue utilizado por la reina María
  Estuardo de Escocia, para conspirar junto con los
  españoles contra su prima Isabel I
• Los mensajes cifrados de María fueron fácilmente
  descifrados mediante sencillos análisis
  estadísticos por los agentes de Isabel I
• Junto con la pérdida del secreto de la
  comunicación, María perdió la cabeza en su
  ejecución el 8 de febrero de 1587.
• Después de esto el cifrado César quedó
  definitivamente descartado como método de cifrado
  seguro para los gobernantes del mundo.
• Desde entonces a hoy, los cifrados usados por
  los estados para preservar sus secretos han
  mejorado considerablemente.

8
Ejemplo de cifrado monoalfabético
Se resolvió por el método de analizar las
frecuencias.
9
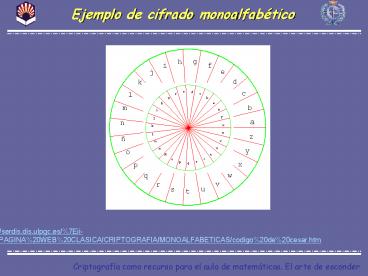
Ejemplo de cifrado polialfabético

• En 1466, León Battista Alberti, músico, pintor,
  escritor y arquitecto, concibió el primer sistema
  polialfabético que se conoce El disco de Alberti
• Cambia de abecedario cada dos o tres palabras.
• El emisor y el destinatario habían de ponerse de
  acuerdo para fijar la posición relativa de dos
  círculos concéntricos, y cada cuantas palabras
  cambiaban de alfabeto
• Los diferentes alfabetos utilizados eran
  representados en los discos pequeños, mientras
  que el grande se rellenaba con el alfabeto normal
  (antes 24 símbolos)

10
Ejemplo de cifrado polialfabético
Usando estos discos vamos a cifrar el mensaje
levántate contra la pobreza
Decisiones a tomar Primer disco a usar es el 1 y
emparejamos a con a Segundo disco a usar es el 2
y emparejamos a con w Cambiamos de disco cada
palabra
uviacpapv
snogmiw
zndxgw
ua
disco1
disco2
Actividad 6
11
Ejemplos

• Actividad 1.9. Cifrado polialfabético

Letras en posición impar Morse Letras en
posición par ASCII
-- 79 .-. 83 . 89 .- 83 -.-. 73 .. MORSEYASCII
12
Cifrado afín

• El cifrado módulo n con claves a y b o cifrado
  afín
• Consiste en aplicar a cada símbolo de nuestro
  abecedario una transformación matemática del tipo
• Símbolo ? a.Símbolo b
• En nuestro lenguaje
• F(x) ax b
• Qué pasos hay que seguir?
• Vamos a explicarlo cifrando el mensaje
• aprendemos a cifrar

13
Cifrado afín

• Paso 1º Seleccionar los símbolos con los que
  vamos a trabajar
• a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o,
  p, q, r, s, t, u, v, w, x, y, z ? Z27
• Se entenderán bien las frases? añadimos espacio
  en blanco, punto y coma
• a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o,
  p, q, r, s, t, u, v, w, x, y, z, , ., , ? Z30
• Seleccionamos los valores de a y b.
• Por ejemplo a 7 y b 5
• Paso 2º Asignar a cada carácter un número

14
Cifrado afín
Paso 3º Pasar el mensaje a cifras

• Paso 4º Trabajar en el conjunto Z30
• Z30 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,
  13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24,
  25, 26, 27, 28, 29

15
Cifrado afín

• Aplicamos la transformación al mensaje, expresado
  en números
• f(x) 7x 5 (mod30)
• 16 7.16 5 112 5 117 27 (mod 30)

16
Cifrado afín

• Pasar de nuevo a letras los números obtenidos
  tras aplicar la transformación

El mensaje aprendemos a cifrar se envía como
fldgzd,trñfñsbklfl
17
Descifrado afín

• Qué datos se necesitan para empezar a descifrar?
• 1. El mensaje cifrado dcldofñdrytñ,dñqcryf
• 2. El conjunto de caracteres Z30
• 3. Las dos claves, que en este caso han sido a
  7 y b 5
• Pasamos el mensaje a números

18
Descifrado afín
Si la función de cifrado ha sido y ax b para
encontrar la función de descifrado se despeja x
pero trabajando en Zn

• Para calcular el opuesto de un número hay que
  resolver la ecuación
• Nº Opuesto n

Para calcular el inverso de un número hay que
resolver la ecuación Nº Inverso 1
Por ejemplo para n 30 y función de cifrado y
7x 5 Y 25 7x X 13(y 25) puesto que 137
1 en Z30
19
Descifrado afín

• Si hemos cifrado con f(X) 7X 5
• desciframos con la función f-1(Y) (Y 25)13
• pero trabajando siempre en Z30
• Por ejemplo 3 ? (3 25)13 364 que en
  Z30 es el 4

20
Descifrado afín

• Pasamos estos números a letras

El mensaje original era Eureka, esto me gusta
21
Criptoanálisis de método afín (módulo 28)
En este cifrado, cada letra se cifrará siempre
igual. Es una gran debilidad y por eso es muy
vulnerable y fácil de atacar
Cifrado Ci (a?Mi b) mod 28 Descifrado Mi
( (Ci b)?a-1)mod 28 donde b es el
opuesto de b en Z28 y a-1 es el inverso de a en
Z28

• Sirven todos los valores de a y b para cifrar un
  mensaje?
• Y para descifrarlo?
• El factor de desplazamiento puede ser cualquiera
  0 ? b ? 27.
• Para que exista el inverso a-1 el factor de
  multiplicación a debe ser primo relativo con el
  número n de elementos que tenga el alfabeto (en
  este caso 28) MCD(a, n) 1

22
Criptoanálisis método afín (módulo 28)
El ataque a este sistema es muy elemental. Se
relaciona el elemento más frecuente del
criptograma a la letra E y el segundo a la letra
A, planteando un sistema de 2 ecuaciones. Si el
texto tiene varias decenas de caracteres este
ataque prospera si el texto es de longitud
pequeña puede haber ligeros cambios en esta
distribución de frecuencias hay que probar con
los distintos valores hasta conseguir un texto
claro con sentido Lo único que necesitamos es
conocer las letras que se suelen repetir con más
frecuencia en cada lenguaje
23
Criptoanálisis de método afín (módulo 28)
Si se intercepta el mensaje pero no se conoce la
clave
Analizamos las frecuencias
1er INTENTO. PIENSO.... B es la que más veces
aparece en el criptograma, puede venir de la E
y la P de la A
Planteamos el sistema de ecuaciones 1 (4?a b)
mod 28 16 (0?a b) mod 28
Al resolver, obtenemos b 16 a?
24
1 (4a16)mod28
Que nunca da como resultado 1, luego no puedo
encontrar a
25
Criptoanálisis de método afín (módulo 28)
Si interceptamos el mensaje pero no conocemos la
clave
Analizamos las frecuencias
2º INTENTO. PIENSO.... B es la que más veces
aparece, puede ser la A y la P la E
Planteamos el sistema 1 (0?a b) mod 28 16
(4?a b) mod 28
obtenemos b 1 a?
26
16 (4?a b) mod 28 ? Mod4a 1, 28
Para a 15 Mod4a 1, 28 5 Para a
16 Mod4a 1, 28 9 Para a 17 Mod4a
1, 28 13 Para a 18 Mod4a 1, 28
17 Para a 19 Mod4a 1, 28 21 Para a
20 Mod4a 1, 28 25 Para a 21
Mod4a 1, 28 1 Para a 22 Mod4a 1,
28 5 Para a 23 Mod4a 1, 28 9
Para a 24 Mod4a 1, 28 13 Para a
25 Mod4a 1, 28 17 Para a 26 Mod4a
1, 28 21 Para a 27 Mod4a 1, 28
25 No sale 16, no es la solución

• Para a 0 Mod4a 1, 28 1
• Para a 1 Mod4a 1, 28 5
• Para a 2 Mod4a 1, 28 9
• Para a 3 Mod4a 1, 28 13
• Para a 4 Mod4a 1, 28 17
• Para a 5 Mod4a 1, 28 21
• Para a 6 Mod4a 1, 28 25
• Para a 7 Mod4a 1, 28 1
• Para a 8 Mod4a 1, 28 5
• Para a 9 Mod4a 1, 28 9
• Para a 10 Mod4a 1, 28 13
• Para a 11 Mod4a 1, 28 17
• Para a 12 Mod4a 1, 28 21
• Para a 13 Mod4a 1, 28 25
• Para a 14 Mod4a 1, 28 1

27
Criptoanálisis de método afín (módulo 28)
Si interceptamos el mensaje pero no se conoce la
clave
Analizamos las frecuencias
DESPUÉS DE VARIOS INTENTOS. PIENSO.... B puede
venir de la E y la N de la A
Planteamos el sistema 1 (4?a b) mod 28 13
(0?a b) mod 28
14a13 (mod 28)
Al resolver, obtenemos b 13 a?
28
14a13 ? Mod4a 13, 28
Y podría ser a 4, a 11, a 18, a 25
29
Criptoanálisis de mensaje afín (módulo 28)
Si interceptamos el mensaje pero no se conoce la
clave
Descifrado Mi (Ci b)?a-1 mod 28 donde
a-1 inverso de a en Z28
Descartamos a 4 y a 18 por no tener inversos
MCD(a, 28) ? 1 puede ser a 11?
puede ser a 25 ?
30
Para practicar

• Puedes cifrar tus mensajes directamente en la
  siguiente dirección
• Ten en cuenta que se está trabajando con un
  alfabeto de 26 letras
• (no puedes usar ñ)
• http//www.apprendre-en-ligne.net/crypto/subst/af
  fine.html
• http//www.math.temple.edu/renault/cryptology/af
  fine.html

31
Hasta ahora conocemos
TRANSPOSICIÓN
ESCÍTALA RUEDA DE JEFFERSON CIFRADO CON
PALNTILLAS
SUSTITUCIÓN
No hay correspondencia única entre el alfabeto
del mensaje y el alfabeto de cifrado
Correspondencia única entre el alfabeto del
mensaje y el alfabeto de cifrado Cesar Afin