Orbital Mechanics

1
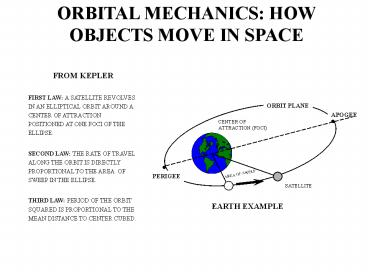
ORBITAL MECHANICS HOW OBJECTS MOVE IN SPACE
FROM KEPLER FIRST LAW A
SATELLITE REVOLVES IN AN ELLIPTICAL ORBIT AROUND
A CENTER OF ATTRACTION POSITIONED AT ONE FOCI OF
THE ELLIPSE. SECOND LAW THE RATE OF TRAVEL
ALONG THE ORBIT IS DIRECTLY PROPORTIONAL TO THE
AREA OF SWEEP IN THE ELLIPSE. THIRD LAW PERIOD
OF THE ORBIT SQUARED IS PROPORTIONAL TO THE MEAN
DISTANCE TO CENTER CUBED.
ORBIT PLANE
APOGEE
CENTER OF ATTRACTION (FOCI)
AREA OF SWEEP
PERIGEE
SATELLITE
EARTH EXAMPLE
2
ORBITAL MECHANICS WHY OBJECTS MOVE THE WAY THEY
DO
NEWTONIAN THEORY Fg G M m / r2 Fc m V2 /
r A SATELLITE MAINTAINS ITS ORBIT WHEN Fc
Fg G UNIVERSAL GRAVITY CONSTANT M MASS OF
EARTH m MASS OF SATELLITE r DISTANCE EARTH
CENTER TO SATELLITE IN NEAR CIRCULAR ORBITS THE
ORBITAL VELOCITY IS ABOUT CONSTANT. IN HIGHLY
ELLIPTICAL ORBITS THE SATELLITE SPEEDS UP TO MAX
VELOCITY AT PERIGEE AND SLOWS DOWN TO MIN
VELOCITY AT APOGEE.
V ORBITAL VELOCITY
ORBITAL PATH
Fc CENTRIPETAL FORCE DUE TO REVOLUTION
ALTITUDE
Fg GRAVITATION FORCE
3
Newtons Laws

• A body remains at rest or in constant motion
  unless acted upon by external forces
• The time rate of change of an objects momentum
  is equal to the applied force
• For every action there is an equal and opposite
  reaction
• The force of gravity between two bodies is
  proportional to the product of their masses and
  inversely proportional to the square of the
  distances between them.

4
Acceleration, Time, Distance

• F ma
• Vf V0 at
• s V0t at2

2
5
Vector Addition
Vector addition is done by adding the two head to
tail vectors to equal the tail to tail and head
to head vector
V3
V1
V2
Law of Sines a / sin A b / sin B c / sin
C Law of Cosines a2 b2 c2 - 2bc Cos A b2
a2 c2 - 2ac Cos B c2 a2 b2 - 2ab Cos C
C
a
b
A
B
c
6
Trigonometric Functions
sine opposite/ hypotenuse y/r cosine
adjacent / hypotenuse x/r tangent opposite /
adjacent y/x
sin 0 0 cos 0 1 sin 90 1 cos 90 0 tan 0
0 tan 90 infinity
-1infinity
y
x
r2 x2 y2 sin2 q cos2 q 1
7
Rocket Engines

• Liquid Propellant
• Mono propellant
• Catalysts
• Bi-propellant
• Solid Propellant
• Grain Patterns
• Hybrid
• Nuclear
• Electric

Performance Energy Safety Simplicity Expanding
Gases Thrust Termination Restart
8
Specific Heat

• Specific Heat the amount of heat that enters or
  leaves a unit mass while the substance changes
  one degree in temperature.
• c Btu per lbsm - degree Rankine
• cp specific heat at constant pressure
• cv specific heat at constant volume
• k ratio of specific heats

9
Specific Impulse
Isp 9.797
Pe Nozzle Exit Pressure (psi) Combustion Chamber Pressure (psi) 6,000 psi Tc
Combustion Chamber Temperature (degrees
Rankine) 5,000o R mg average molecular weight
of combustion products (lb/mole)
2H2O 2 2H2O 18 lbs/mole mg
10
Launch Velocity Losses

• Gravity losses
• Pitch over to get correct velocity vector
  alignment for orbital insertion
• Drag from atmosphere
• Not instantaneous application of velocity

Losses are between 15 and 17 of DV
11
Rocket Formulas
Rocket Equation
DV Isp x g x ln MR
Mass Ratio
Specific Impulse
Thrust
12
Three Stage Booster
All three stages
DV1 (280)(32.2)ln (2.56) 8,475 ft/sec DV2
(290)(32.2)ln (2.69) 9,238 ft/sec DV3
(250)(32.2)ln (4.57) 12,232 ft/sec
Vl 29,945 ft/sec
Vposigrade 29,535 ft/sec Vretrograde 30,183
ft/sec
Can place payload in posigrade orbit, but not in
retrograde orbit,
13
ORBIT FORMULAS
ELLIPTICAL CIRCULAR ORBITS

a
2a rA rP


b
c
rA
eccentricity

e
rP

Apogee
Perigee
a
c
rP
c a -
a - rP
e

r
r
a
b
rP
e 1 -
a
c
1 - 2rP
e
rA rP
rA - rP
e

rA rP
14
CONSTANTS FOR ORBIT
PHYSICAL
m
GEOMETRIC
E Specific Energy H Specific Momentum
e
a b c
Universal gravitational attraction
mr
m2
r
n
e
E 0 for a circle
V
e
E m1
Trajectory m2
e
1 for a parabola
m
e

1 for a hyperbola

r
1
2EH2
m
1
cos n
Polar coordinates for any conic section pages
32, 33, 34 Handout
2
m
H2
e
k

e

2EH2
1
2
15
Orbital Period
CIRCULAR ORBIT
ELLIPTICAL ORBIT
2 p a
2 p r
P

Period

V
V
m
a mean distance from focus semi
major axis
V

r
4
r 2
p
2
P2

P2

m
m
r
KEPLERS THIRD LAW
4
r 3
p
2
P2

P2
(2.805 x 1015)a3
m
sec2
units

ft3
16
EARTH SATELLITES
Eccentricity
e
rp a - c ra a c rp ra
2a
Major Axis 2a Minor Axis 2b
c a

e
E specific energy H specific angular
momentum
m
c2 a2 - b2

E V2
M
(1)

m
2
2a
r
m
m
H Vr cos

V
r

for elliptical orbits from (1)
2
-
V

r
a
17
Coordinate Systems

• Cartesian Coordinates
• Abscissa x
• Ordinate y
• (x,y)

• Polar Coordinates
• Radius Vector r
• Vectorial Angle q
• (r,q)

r
q
18
Description of Orbit

• Right Ascension
• Measured eastward from the vernal equinox
• In Spring when the suns center crosses the
  equatorial plane once thought to be aligned with
  the first point of the constellation Aries
• Inclination
• Argument of Perigee
• Two of the following
• Eccentricity
• Perigee
• Apogee

19
Orbit Calculations
Ellipse is the curve traced by a point moving in
a plane such that the sum of its distances from
the foci is constant.
ra
rp
r
r
c
r r 2a
a2 b2 c2
20
INCLINATION
FUNCTION OF LAUNCH AZIMUTH AND LAUNCH SITE
LATITUDE
cos i (inclination) cos (latitude) sin
(azimuth)
N
North 0 degrees Azimuth
AZIMUTH
azimuth
90o
cos i cos (lat) sin (az)
East
West
lat.
sin 90o 1 sin 0o 0 sin 180o
0 sin 270o -1
180o
South
launch azimuth from 180o to360o retrograde
orbit launch azimuth from 0o to 180o
posigrade orbit
S
21
Celestial Sphere
22
(No Transcript)
23
ORBITAL MECHANICS SPECIFIC ORBITS AND
APPLICATIONS

• POLAR (100- 700 NM AT 80 - 100 DEG. INCLINATION)
• SATELLITE PASSES THROUGH THE EARTH'S SHADOW AND
  PERMITS VIEWING OF THE ENTIRE EARTHS SURFACE
  EACH DAY WITH A SINGLE SATELLITE
• SUN SYNCHRONOUS (80 - 800 NM AT 95 - 105 DEG
  INCLINATION)
• PROCESSION OF ORBITAL PLANE SYNCHRONIZED WITH THE
  EARTHS ROTATION SO SATELLITE IS ALWAYS IN VIEW
  OF THE SUN
• PERMITS OBSERVATION OF POINTS ON THE EARTH AT THE
  SAME TIME EACH DAY
• SEMISYNCHRONOUS (10,898 NM AT 55 DEG INCLINATION)
  
• 12 HR PERIODS PERMITTING IDENTICAL GROUNDTRACES
  EACH DAY
• HIGHLY INCLINED ELLIPTICAL (FIXED PERIGEE
  POSITION)
• SATELLITE SPENDS A GREAT DEAL OF TIME NEAR THE
  APOGEE COVERING ONE HEMISPHERE
• CLASSICALLY CALLED MOLNIYA ORBIT BECAUSE OF ITS
  HEAVY USE BY THE RUSSIANS FOR NORTHERN
  HEMISPHERE COVERAGE
• GEOSYNCHRONOUS (GEO) (CIRCULAR, 19,300 NM AT 0
  DEG INCLINATION)
• 24 HR PERIOD PERMITS SATELLITE POSITIONING OVER
  ONE POINT ON EARTH.
• ORBITAL PERIOD SYNCHRONIZED WITH THE EARTHS
  ROTATION (NO OTHER ORBIT HAS THIS FEATURE)

24
Linear and Angular Motion
ANGULAR MOTION
LINEAR MOTION
Distance
S r q ft
Velocity
Acceleration
(1 radian 57.3 degrees)
25
s r
Q
r
s
radians
Q
26
CONSERVATION OF
ENERGY
MOMENTUM
m r
V2 2
Angular Momentum mr2w
constant F
-

Specific Energy
mr2w constant mH
H V r cos f
Specific Angular Momentum
Vr
f

V
Specific means per 1b mass
27
CONSTANTS FOR ORBIT
PHYSICAL
m
GEOMETRIC
E Specific Energy H Specific Momentum
e
a b c
Universal gravitational attraction
mr
m2
r
n
e
E
0 for a circle
V
e
E

m1
Trajectory m2
e
1 for a parabola
m
e

1 for a hyperbola

r
1
2EH2
m
1
cos n
2
m
H2
e
k

e

2EH2
1
2
28
CENTRIPETAL ACCELERATION
but for circular orbit Vr 0
A -- VrDt
(
)
ar
Dt 2
2
r
r2 (VtDt) 2

2
VtDt
ar2
Dt 4

r2 r ar D t2

r2 Vt 2 Dt 2
A
4
subtract r2 from each side of the equation
ar2
Dt 4
r ar D t2

Vt2 Dt 2
r
4
r
divided by D t2
Vt2
rar

D t
as
0
or
then
29
ESCAPE VELOCITY
E 0
V2 2 r
E1
V2
0
r
2
m
Vescape

36,700