Depth-First Search

1
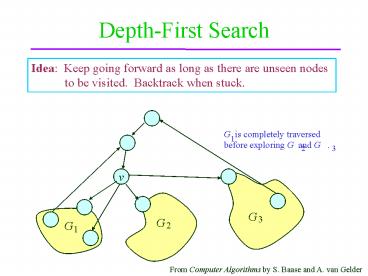
Depth-First Search
Idea Keep going forward as long as there are
unseen nodes to be visited.
Backtrack when stuck.
v
G
3
G
G
2
1
From Computer Algorithms by S. Baase and A. van
Gelder
2
The DFS Algorithm
DFS(G) time ? 0 //
global variable for each v ? V(G) do
disc(v) ? unseen for each v ? V(G) do
if disc(v) unseen then
DFS-visit(v) DFS-visit(v) time ?
time 1 disc(v) ? time for each u ?
Adj(v) do if disc(u) unseen then
DFS-visit(u)
3
A DFS Example
time 1
a
i
h
c
e
d
j
f
l
k
g
b
2
3
4
Recursive DFS Calls
DFS(G) DFS-visit(a) DFS-visit(b)
DFS-visit(g)
DFS-visit(e) DFS-visit(f)
DFS-visit(c) DFS-visit(d)
DFS-visit(h) DFS-visit(i)
DFS-visit(j) DFS-visit(k)
DFS-visit(l)
1
a
c
e
d
4
6
7
5
f
2
3
g
b
8
9
i
h
10
j
l
k
DFS-visit(v) explores every unvisited
vertex reachable from v before it returns.
12
11
5
Depth-First Search Forest
a
i
h
c
e
d
j
f
l
k
g
b
Edges that, during DFS, lead to an unexplored
vertex form a depth-first search forest.
6
Running Time of DFS
?(V E)
7
Edge Classification Undirected Graphs
1. Tree edges are those in the DFS forest.
2. Back edges go from a vertex to one of its
ancestors.
a
h
j
b
d
c
i
k
g
l
e
f
8
Edge Classification Directed Graphs
Besides tree edges and back edges, there are also
3. Forward edges go from a vertex to one of its
descendants.
4. Cross edges all other edges.
a
h
b
c
g
d
e
i
9
Applications of DFS
In O(V E) time, we can
10
Back Edge
Theorem A directed graph G has a cycle if and
only if its DFS forest has a
back edge.
? A back edge leads to a cycle.
Proof
? Suppose there is a cycle. Let u be the
vertex with the smallest time stamp on the
cycle and v be the predecessor of u in the
cycle.
Therefore at the time of visiting v, a back edge
(v, u) will be found.
The theorem also applies to an undirected graph.
11
Algorithm for Detecting Cycle
(v, u) is a back edge if v is a descendant of u
in the DFS tree.
for each u ? V do onpath(u) ? false // on
path from the root of the DFS tree
DFS-visit(v) time ? time 1 disc(v) ?
time onpath(v) ? true for each u ?
Adj(v) do if disc(u) unseen then
DFS-visit(u) else if onpath(u) then
a cycle has been found halt
onpath(v) ? false // backtrack v no longer on
path from root
12
Topological Sort of Digraphs
Ordering lt over V(G) such that u lt v whenever (u,
v) ? E(G).
13
Intuition Precedence Diagram
14
Existence of Topological Sort
Lemma G can be topologically sorted iff it has
no cycle, that is, iff it is a
dag (directed acyclic graph).
? If G has a cycle, then it cannot be
topologically sorted.
Proof
? If G has no cycle, then it can be topologically
sorted.
Constructive proof An algorithm that sorts any
dag.
15
Algorithm for Topological Sort
DFS-visit-topo(v) time ? time 1
disc(v) ? time for each u ? Adj(v) do if
disc(u) unseen then DFS-visit-topo(u)
L ? insert(v, L) // insert v in the
front of L
16
Correctness of the Algorithm
Claim Let G be a directed acyclic graph (dag).
If (u, v) ? E(G), then
DFS-visit-topo(u) finishes after
DFS-visit-topo(v).
Proof Consider the time when DFS-visit-topo(u)
first scans (u, v)
Case 1 DFS-visit-topo(v) has already finished.
Obviously, DFS-visit-topo(u) finishes
afterwards. And (u, v) is a cross edge.
Case 2 DFS-visit-topo(v) has already started,
but not yet finished.
Then (u, v) is a back-edge and G has a cycle,
contradicting that it is a dag!
17
Correctness (contd)
Case 3 DFS-visit-topo(v) has not yet started.

Then the procedure call will start immediately.
So (u, v) is a tree edge. Hence
DFS-visit-topo(u) will finish after
DFS-visit-topo(v).
Combining cases 1 and 3, u will always be
inserted in front of v in the queue L.
Theorem If G is a dag, then at termination of
DFS, L is a topological ordering
of V(G).
Courtesy Dr. Fernandez-Baca