Kapitel 4 / 1

1
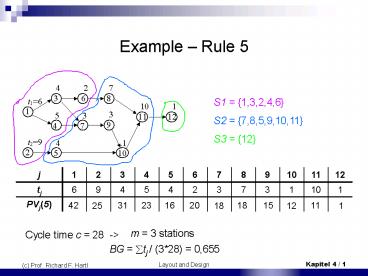
Example Rule 5
S1 1,3,2,4,6 S2 7,8,5,9,10,11 S3 12
j 1 2 3 4 5 6 7 8 9 10 11 12
tj 6 9 4 5 4 2 3 7 3 1 10 1
PVj(5)
42
31
23
16
20
18
11
15
25
18
1
12
m 3 stations
Cycle time c 28 -gt
BG ?tj / (328) 0,655
2
Example Regel 7, 6 und 2

• 3

j 1 2 3 4 5 6 7 8 9 10 11 12
PVj(7)
PVj(6)
PVj(2)
1
2
1
2
2
2
2
2
2
2
2
2
1
1
1
1
1
1
1
1
1
2
2
2
1
1
10
3
2
6
9
4
5
4
3
7
Apply rule 7 (latest possible station) at
first If this leads to equally prioritized
operatios -gt apply rule 6 (minimum number of
stations for j and all predecessors) If this
leads to equally prioritized operatios -gt appyl
rule 2 (decreasing processing times tj)
Solution c 28 ? m 2 BG 0,982 S1
1,3,2,4,5 S2 7,9,6,8,10,11,12
3
More heuristic methods

• Stochastic elements for rules 2 to 7
• Random selection of the next operation (out of
  the set of operations ready to be applied)
• Selection probabilities proportional or
  reciprocally proportional to the priority value
• Randomly chosen priority rule
• Enumerative heuristics
• Determination of the set of all feasible
  assignments for the first station
• Choose the assignment leading to the minimum idle
  time
• Proceed the same way with the next station, and
  so on (greedy)

4
Further heuristic methods

• Heuristics for cuttingpacking problems
• Precedence conditions have to be considered as
  well
• E.g. generalization of first-fit-decreasing
  heuristic for the bin packing problem.
• Shortest-path-problem with exponential number of
  nodes
• Exchange methods
• Exchange of operations between stations
• Objective improvement in terms of the
  subordinate objective of equally utilized stations

5
Worst-Case analysis of heuristics

• Solution characteristics for integer c and tj
• (j 1,...,n) for alternative 2
• ? Total workload of 2 neigboured stations has to
  exceed the cycle time
• Worst-Case bounds for the deviation of a solution
  with m
• Stations from a solution with m stations

m/m ? 2 - 2/m for even m and m/m ? 2 - 1/m
for odd m m lt c?m/(c - tmax 1) 1
6
Determination of cyle time c

• Given number of stations
• Cycle time unknown
• Minimize cycle time (alternative 1) or
• Optimize cycle time together with the number of
  stations trying to maximize the systems
  efficiency (alternative 3).

7
Iterative approach for determination of minimal
cycle time

1. Calculate the theoretical minimal cycle
   time(or cmin tmax if this is larger) and
   c cmin
2. Find an optimal solution for c with minimum m(c)
   by applying methods presented for alternative 1
3. If m(c) is larger than the given number of
   stations increase c by ? (integer value) and
   repeat step 2.

8
Iterative approach for determination of minimal
cycle time

• Repeat until feasible solution with cycle time ?
  c and number of stations ? m is found
• If ? gt 1, an interval reduction can be applied
  if for c a solution with number of stations ? m
  has been found and for c-? not, one can try to
  find a solution for c-?/2 and so on

9
Example rule 5

• m 5 stations
• Find maximum production rate, i.e. minimum
  cycle time

j 1 2 3 4 5 6 7 8 9 10 11 12
tj 6 9 4 5 4 2 3 7 3 1 10 1
PVj(5) 42 25 31 23 16 20 18 18 15 12 11 1
cmin ?tj/m 55/5 11 (11 gt tmax 10)
10
Example rule 5

• Solution c 11
• 1,3, 2,6, 4,7,9, 8,5, 10,11, 12
• Needed 6 gt m 5 stations
• ? c 12, assign operation 12 to station 5
• ? S5 10,11,12

For larger problems usually, c leading to an
assignment for the given number of stations, is
much larger than cmin. Thus, stepwise increase of
c by 1 would be too time consuming -gt increase by
? gt 1 is recommended.
11
Classification of complex line balancing problems

• Parameters
• Number of products
• Assignment restrictions
• Parallel stations
• Equipment of stations
• Station boundaries
• Starting rate
• Connection between items and transportation
  system
• Different technologies
• Objectives

12
Number of products

• Single-product-models
• 1 homogenuous product on 1 assembly line
• Mass production, serial production
• Multi-product models
• Combined manufacturing of several products on 1
  (or more) lines.
• Mixed-model-assembly Products are variations
  (models) of a basic product ? they are processed
  in mixed sequence
• Lot-wise multiple-model-production Set-up
  between production of different products is
  necessary ? Production lots (the line is
  balanced for each product separately) ?
  Lotsizing and scheduling of products ? TSP

13
Assignment restrictions

• Restricted utilities
• Stations have to be equipped with an adequate
  quantity of utilities
• Given environmental conditions
• Positions
• Given positions of items within a station? some
  operation may not be performed then (e.g.
  underfloor operations)
• Operations
• Minimum or maximum distances between 2 operations
  (concerning time or space)
• ? 2 operations may not be assigned to the same
  station
• Qualifications
• Combination of operations with similiar complexity

14
Parallel stations

• Models without parallel stations
• Heterogenuous stations with different operations
  ? serial line
• Models with parallel stations
• At least 2 stations performing the same operation
• Alternating processing of 2 subsequent operations
  in parallel stations
• Hybridization Parallelization of operations
• Assignment of an operation to 2 different
  stations of a serial line

15
Equipment of stations

• 1-worker per station
• Multiple workers per station
• Different workloads between stations are possible
• Short-term capacity adaptions by using jumpers
• Fully automated stations
• Workers are used for inspection of processes
• Workers are usually assigned to several stations

16
Station boundaries

• Closed stations
• Expansion of station is limited
• Workers are not allowed to leave the station
  during processing
• Open stations
• Workers my leave their station in (rechtsoffen)
  or in reversed (linksoffen) flow direction of
  the line
• Short-term capacity adaption by under- and
  over-usage of cycle time.
• E.g. Manufacturing of variations of products

17
Starting rate

• Models with fixed statrting rate
• Subsequent items enter the line after a fixed
  time span.
• Models with variable starting rate
• An item enters the line once the first station of
  the line is idle
• Distances between items on the line may vary (in
  case of multiple-product-production)

18
Connection between items and transportation
systems

• Unmoveable items
• Items are attached to the transportation system
  and may not be removed
• Maybe turning moves are possible
• Moveable items
• Removing items from the transportation system
  during processing is
• Post-production
• Intermediate inventories
• Flow shop production without fixed time
  constraints for each station

19
Different technologies

• Given production technologies
• Schedules are given
• Different technologies
• Production technology is to be chosen
• Different alternative schedules are given
  (precedence graph) and/or
• different processing times for 1 operation

20
Objectives

• Time-oriented objectives
• Minimization of total cycle time, total idle
  time, ratio of idle time, total waiting time
• Maximization of capacity utilization (systems
  efficieny) most relevant for (single-product)
  problems
• Equally utilized stations
• Further objectives
• Minimization of number of stations in case of
  given cycle time
• Minimization of cycle time in case of given
  number of stations
• Minimization of sum of weighted cycle time and
  weighted number of stations

21
Objectives

• Profit-oriented approaches
• Maximization of total marginal return
• Minimization of total costs
• Machines- and utility costs (hourly wage rate of
  machines depends on the number of stations)
• Labour costs often identical rates of labour
  costs for all workers in all stations)
• Material costs defined by output quantity and
  cycle time
• Idle time costs Opportunity costs depend on
  cycle time and number of stations

22
Multiple-product-problems

• Mixed model assemblySeveral variants of a basic
  product are processed in mixed sequence on a
  production line.
• Processing times of operations may vary between
  the models
• Some operations may not be necessary for all of
  the variants
• ? Determination of an optimal line balancing and
  of an optimal sequence of models.

23

• multi-model
• Lot-wisemixed-model
• production
• With machine set-up

24

• mixed-model
• Without set-up
• Balancing for a theoretical average model

25
Balancing mixed-model assembly lines

• Similiar models
• Avoid set-ups and lot sizing
• Consider all models simultaneously
• Generalization of the basic model
• Production of p models of 1 basic model with up
  to n operations production method is given
• Given precedence conditions for operations in
  each model j 1,...,n ? aggregated precendence
  graph for all models
• Each operation is assigned to exactly 1 station
• Given processing times tjv for each operation j
  in each model v
• Given demand bv for each model v
• Given total time T of the working shifts in the
  planning horizon

26
Balancing mixed-model assembly lines

• Total demand for all models in planning horizon
• Cumulated processing time of operation j over
  all models in planning horizon

27
LP-Model

• Aggregated model
• Line is balanced according to total time T of
  working shifts in the planning horizon.
• Same LP as for the 1-product problem, but cycle
  time c is replaced by total time T

28
LP-Model

• Objective function

number of the last station (job n)
Constraints for all j 1, ... , n ... Each
job in 1 station for all k 1, ... , ...
Total workload in station k for all ...
Precedence conditions for all j and k
29
Example
v 1, b1 4 v 2, b2 2
v 3, b3 1 aggregated model
30
Example

• Applying exact method
• given T 70
• Assignment of jobs to stations with m 7
  stationsS1 1,3S2 2 S3 4,6,7 S4
  8,9 S5 5,10 S6 11 S7 12

31
Parameters

• ... Workload of station k for model v in T
• ... Average workload of m stations for model v
  in T
• Per unit
• ... Workload of station k for 1 unit of
  model v
• ... Avg. workload of m stations for 1 unit of
  model v
• Aggregated over all models
• ... Total workload of station k in T

32
Example parameters per unit
?kv       Station k       Avg.
Model v 1 2 3 4 5 6 7 ?v
1 10 7 11 10 6 10 1 7,86
2
3
x 4
x 2
7
8
4
0
7,43
11
11
11
8
13
12
14
3
8
3
8,71
x 1
33
Example - Parameters
?kv       Station k       Avg.
Model v 1 2 3 4 5 6 7 ?v
1 40 28 44 40 24 40 4 31,43
2
3
t(Sk) 70 63 70 70 35 70 7 55
22
8
22
14
16
0
14,86
22
8
12
13
14
3
8
3
8,71
34
Conclusion

• Station 5 and 7 are not efficiently utilized
• Variation of workload ?kv of stations k is higher
  for the models v as for the aggregated model
  t(Sk)
• Parameters per unit show a high degree of
  variation for the models. Model 3, for example,
  leads to an high utilization of stations 2, 3,
  and 4.
• If we want to produce several units of model 3
  subsequently, the average cycle time will be
  exceeded -gt the line has to be stopped

35
Avoiding unequally utilized stations

• Consider the following objectives
• Out of a set of solutions leading to the same
  (minimal) number of stations m (1st objective),
  choose the one minimizing the following 2nd
  objective
• ...Sum of absolute deviation in utilization
• Minimization by, e.g., applying the following
  greedy heuristic

36
Thomopoulos heuristic

• Start Deviation ? 0, k 0
• Iteration until not-assigned jobs are available
• increase k by 1
• determine all feasible assignments Sk for the
  next station kchoose Sk with the minimum sum of
  deviation
• ? ? ?(Sk)

37
Thomopoulos example

• T 70
• m 7
• Solution
• 9 stations (min. number of stations 7)
• S1 1, S2 3,6, S3 4,7, S4 8, S5
  2,
• S6 5,9, S7 10, S8 11, S9 12
• Sum of deviation ? 183,14

38
Thomopoulos heuristic

• Consider only assignments Sk where workload t(Sk)
  exceeds a value ? (i.e. avoid high idle times).
• Choose a value for ?
• ? small
• well balanced workloads concerning the models
• Maybe too much stations
• ? large
• Stations are not so well balanced
• Rather minimum number of stations very large ? ?
  maybe no feasible assignment with t(Sk) ? ?

39
Thomopoulos heuristic Example

• ? 49
• Solution
• 7 stations
• S1 2, S2 1,5, S3 3,4, S4
  7,9,10, S5 6,8, S6 11, S7 12
• Sum of deviation ? 134,57

40
Exact solution

• 7 stations
• S1 1,3, S2 2, S3 4,5, S4 6,7,9 ,
  S5 8,10, S6 11, S7 12
• Sum of deviation ? 126

?kv       Station k       Avg.
Modelv 1 2 3 4 5 6 7 ?v
1 40 28 40 36 32 40 4 31,43
2 22 22 16 12 10 22 0 14,86
3 8 13 7 8 14 8 3 8,71
t(Sk) 70 63 63 56 56 70 7 55
41
Further objectives

• Line balancing depends on demand values bj
• Changes in demand ? Balancing has to be reivsed
  and further machine set-ups have to be considered
• Workaround
• Objectives not depending on demand
• sum of absolute deviations in utilization
  per unit

42
Further objectives

• Disadvantages of this objective
• Large deviations for a station (may lead to
  interruptions in production). They may be
  compensated by lower deviations in other stations
• ? ... Maximum deviation in utilization per
  unit