EECS 40

1
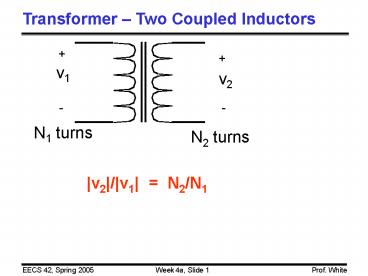
Transformer Two Coupled Inductors


v1
v2
-
-
N1 turns
N2 turns
v2/v1 N2/N1
2
AC Power System

3
Summary of Electrical Quantities
Quantity Variable Unit UnitSymbol Typical Values DefiningRelations ImportantEquations Symbol
Charge Q coulomb C 1aC to 1C magnitude of 6.242 1018 electron charges qe -1.602x10-19 C i dq/dt
Current I ampere A 1mA to 1kA 1A 1C/s
Voltage V volt V 1mV to 500kV 1V 1N-m/C
4
Summary of Electrical Quantities (concluded)
Power P watt W 1mW to 100MW 1W 1J/s P dU/dt PIV
Energy U joule J 1fJ to 1TJ 1J 1N-m U QV
Force F newton N   1N 1kg-m/s2  
Time t second s    
Resistance R ohm W 1W to 10MW V IR P V2/R I2R R
Capacitance C farad F 1fF to 5F Q CV i C(dv/dt)U (1/2)CV2 C
Inductance L henry H 1mH to 1H v L(di/dt) U (1/2)LI2 L
5
Types of Circuit Excitations and Their Uses

• Steady excitation (DC) steady DC voltage or
• current sources. Uses the DC part of all
  kinds
• of communications, transistor, sensor,
  circuits
• Transient excitation -- DC voltage or current
  sources
• are suddenly turned on or off. Uses flashbulb
• circuit where charge a capacitor and suddenly
  dis-
• charge it through flashbulb put an on and an
  off
• switching together and get a digital pulse

• Sinusoidal excitation (AC) Uses AC power
• systems communication systems to find frequency
• response.

6
First-Order Circuits

• A circuit which contains only sources, resistors
  and an inductor is called an RL circuit.
• A circuit which contains only sources, resistors
  and a capacitor is called an RC circuit.
• RL and RC circuits are called first-order
  circuits because their voltages and currents are
  described by first-order differential equations.

R
R
i
i

vs

vs
L
C
7

• The natural response of an RL or RC circuit is
  its behavior (i.e. current and voltage) when
  stored energy in the inductor or capacitor is
  released to the resistive part of the network
  (containing no independent sources).
• The step response of an RL or RC circuit is its
  behavior when a voltage or current source step is
  applied to the circuit, or immediately after a
  switch state is changed.

8
Natural Response of an RL Circuit

• Consider the following circuit, for which the
  switch is closed for t lt 0, and then opened at t
  0
• Notation
• 0 is used to denote the time just prior to
  switching
• 0 is used to denote the time immediately after
  switching
• The current flowing in the inductor at t 0 is
  Io

t 0
i
v
L
Ro
R
Io
9
Solving for the Current (t ? 0)

• For t gt 0, the circuit reduces to
• Applying KVL to the LR circuit
• Solution

i
v
L
Ro
R
Io
10
Solving for the Voltage (t gt 0)
v
L
Ro
R
Io

• Note that the voltage changes abruptly

11
Time Constant t

• In the example, we found that
• Define the time constant
• At t t, the current has reduced to 1/e (0.37)
  of its initial value.
• At t 5t, the current has reduced to less than
  1 of its initial value.

12
Transient vs. Steady-State Response

• The momentary behavior of a circuit (in response
  to a change in stimulation) is referred to as its
  transient response.
• The behavior of a circuit a long time (many time
  constants) after the change in voltage or current
  is called the steady-state response.

13
Review (Conceptual)

• Any first-order circuit can be reduced to a
  Thévenin (or Norton) equivalent connected to
  either a single equivalent inductor or capacitor.
• In steady state, an inductor behaves like a short
  circuit
• In steady state, a capacitor behaves like an open
  circuit

RTh

VTh
C
L
RTh
ITh
14
Natural Response of an RC Circuit

• Consider the following circuit, for which the
  switch is closed for t lt 0, and then opened at t
  0
• Notation
• 0 is used to denote the time just prior to
  switching
• 0 is used to denote the time immediately after
  switching
• The voltage on the capacitor at t 0 is Vo

t 0
Ro
v
?
R
Vo
C
15
Solving for the Voltage (t ? 0)

• For t gt 0, the circuit reduces to
• Applying KCL to the RC circuit
• Solution

i
v
Ro
?
C
R
Vo
16
Solving for the Current (t gt 0)
i
v
Ro
?
C
R
Vo

• Note that the current changes abruptly

17
Time Constant t

• In the example, we found that
• Define the time constant
• At t t, the voltage has reduced to 1/e (0.37)
  of its initial value.
• At t 5t, the voltage has reduced to less than
  1 of its initial value.

18
Natural Response Summary

• RL Circuit
• Inductor current cannot change instantaneously
• time constant

• RC Circuit
• Capacitor voltage cannot change instantaneously
• time constant

i
v
R
L
R
C