Layer Extraction with a Bayesian Model of Shapes - PowerPoint PPT Presentation

Title: Layer Extraction with a Bayesian Model of Shapes


1
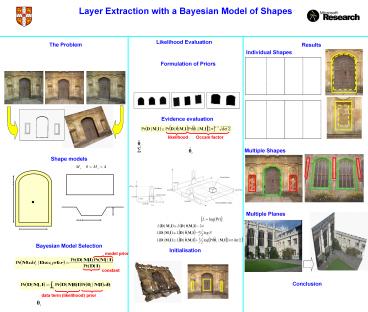
Layer Extraction with a Bayesian Model of Shapes

Philip H. S. Torr1 Anthony Dick2 Roberto
Cipolla21 - Microsoft Research, Cambridge 2 -
Department of Engineering, University of
Cambridge, UK
Likelihood Evaluation
The Problem
Results

• Project model into each image
• Assume image intensities subject to Gaussian noise

• Accurate recovery of depth for all points in an
  image
• Resolve ambiguities using prior knowledge of
  scene
• Obtain dense 3D surface and texture from few
  images

Individual Shapes
AIC
BIC
Occam
Model
Formulation of Priors
2.5829
2.5850
2.5870
Rectangle

• Individual shape priors are uniform over a closed
  region
• Hyperpriors express belief about relation of
  shapes
• Eg Hyperprior expressing that shapes may occur in
  rows

2.5632
2.5657
2.5678
Arch
2.5821
2.5842
2.5872
Bev. Rect.
2.5634
2.5662
2.5691
Bev. Arch
AIC
BIC
Occam
Model
Samples from a hyperprior for rows of shapes
8.2213
8.2536
8.2704
Rectangle
Evidence evaluation
8.2183
8.2453
8.2789
Arch
8.1153
8.1524
8.1750
Bev. Rect.
8.1155
8.1582
8.1785
Bev. Arch
likelihood
Occam factor
AIC, BIC and Occam Factor evidence for each shape
model, plus best fit shape
Untextured textured views of 3D model
is the maximum likelihood parameter vector
for model Mi is the covariance matrix at

Multiple Shapes

• Occam factor approximates volume of prior
  probability space
• occupied by maximum likelihood peak

Shape models

• Select one of a family of shapes

M1 Rectangle c 0, r 0 M2 Arch
r 0 M3 Bev. Rect c 0 M4 Bev Arch
no constraints
c
b
Rows of layers are automatically detected
(x,y)
Occam factors for one and two variables
d
Multiple Planes
(x,y)

• Comparison with other evidence metrics
• AIC
• BIC
• Occam factor

a
r
a
Frontal View
Overhead View
Bayesian Model Selection
Initialisation

• Bayes Rule, expressing probability of a model

model prior
From parallax-based correspondence algorithm
constant

• Model selection depends mainly on the evidence
• Where are the parameters of model i

Automatic layer extraction
Conclusion

• Use of parameterised shapes simplifies structure
  recovery
• Bayesian framework provides principled way of
  utilising
• prior shape models

data term (likelihood)
prior
Initial reconstruction
Initial Layers