Jan 27, 2003

1
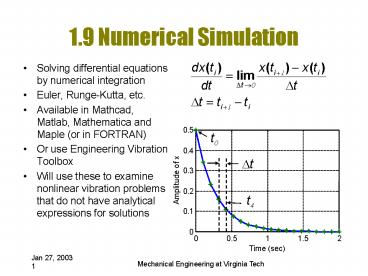
1.9 Numerical Simulation

• Solving differential equations by numerical
  integration
• Euler, Runge-Kutta, etc.
• Available in Mathcad, Matlab, Mathematica and
  Maple (or in FORTRAN)
• Or use Engineering Vibration Toolbox
• Will use these to examine nonlinear vibration
  problems that do not have analytical expressions
  for solutions

0.5
0.4
0.3
Amplitude of x
0.2
0.1
0
0
0.5
1
1.5
2
Time (sec)
2
First order differential equation
x3 will be used to calculate the next term x4
amplitude
The new value of x is calculated from the old
value of x.
Time (sec)
3
Example 9.7.1 solve dx/dt-3x, x(0)1
Numerical solution
Note that the numerical Solution is different for
Each choice of Dt
Analytical solution
4
Time step

• With time step at 0.5 sec the numerical solution
  oscillates about the exact solution
• Large errors can be caused by choosing the time
  step to be too small
• Small time steps require more computation

1
D
Numerical solution
t0.5sec
D
Numerical solution
t0.05sec
Exact solution
0.5
Amplitude of x
0
-0.5
0
1
2
3
4
Time (sec)
5
Numerical solution of the 2nd order equation of
vibration
It is necessary to convert the second order
equation into two first order equations. To
achieve this two new variables x1 and x2 are
defined as follows.
From this two first order differential equations
can be written.
6
Matrix form
Combining these first order DEs in matrix form
gives.
State vector
State matrix
The Euler numerical method can then be applied to
the matrix form to give.
7
Matlab Solutions ode23 and ode45

• Use Runge-Kutta. More sophisticated than the
  Euler method but more accurate
• Often picks Dt (i.e. if solution x(t) is rapidly
  changing Dt is chosen to be small and visa-versa
• Works for nonlinear equations too

Create Matlab function
In the command window
t00tf20 x00 0.25
t,xode45('sdof',t0 tf,x0) plot(t,x)
function xdotsdof(t,x) k2c1m3 A0 1-k/m
-c/m xdotAx
Saved as sdof.m
8
Resulting solution
0.3
Displacement
Velocity
0.2
0.1
Amplitude
0
-0.1
-0.2
0
5
10
15
20
Time (sec)
9
Why use numerical simulation when we can compute
the analytical solution and plot it?

• To have a tool that we are confident with that
  will allow us to solve for the response when an
  analytical solution cannot be found
• Nonlinear systems to not have analytical
  solutions, but can be simulated numerically

10
Section 1.10 Coulomb Friction and the Pendulum

• Nonlinear phenomenon in vibration analysis

11
Vibration of Nonlinear Systems
The force due to Coulomb friction opposes motion,
hence the sgn function is used. The force is
proportional to the normal force and independent
of the velocity of the mass.
12
The sgn function is nonlinear

• Causes equation of motion to be nonlinear
• Can solve as piecewise linear (see text)
• Can solve numerically
• Has more than one equilibrium position
• Decay is linear rather then exponential

0.3
0.2
0.1
Displacement x
0
-0.1
-0.2
0
5
10
15
20
25
Time (sec)
Does not settle at x0
Linear decay
13
General second order system
The equilibrium position is defined
For Coulomb friction this is defined as
i.e. the positions where the force due to the
spring can no longer overcome the sliding
friction force
14
Calculating the equilibrium position for
nonlinear DEs
Equation of motion
Equilibrium positions
Multiple equilibrium positions possible
15
The pendulum
Stable Equilibrium q 0, 2p, 4p ...
Unstable Equilibrium q p, 3p, 5p...
16
Solution to the pendulum

• Can use numerical simulation to examine both
  linear and nonlinear response
• Let (g/L)(0.1)2 so that wn 0.1
• a) use q(0)0.3 rad initial vel 0.3 rad/s
• b) change the initial position to q(0) p rad
  which is near the unstable equilibrium

(b)
(a)
1.5
30
Non-linear
Non-linear
1
Linear
Linear
20
0.5
)
)
q
q
0
10
Angle (
Angle (
-0.5
0
-1
-1.5
-10
0
10
20
30
40
50
0
10
20
30
40
50
Time (sec)
Time (sec)
17
Pendulum with friction added
15
After making a single loop the pendulum cannot
make a second rotation and settles to the stable
equilibrium position of q4p
q4p
10
Angle (q)
Friction loss causes slow decay
5
0
0
20
40
60
80
Time (sec)
18
Summary of Nonlinear Vibrations

• Additional phenomena over linear case
• Multiple equilibrium
• Instabilities possible with positive coefficients
• Form of response dependent on initial conditions
• Closed form solutions usually not available
• Can simulate numerically
• Linear model has tremendous advantages
• Linear combination of inputs yields linear
  combination of outputs
• Linear ode techniques very powerful
• But dont make a design error by ignoring
  important nonlinear situations
• All systems have nonlinear ranges of operation
• Need to sort out when nonlinearity is important
  to consider and when to ignore it

19
Chapter 2 Response to Harmonic Excitation

• Introduces the important concept of resonance

20
2.1 Harmonic Excitation of Undamped Systems

• Consider the usual spring mass damper system with
  applied force F(t)F0coswt
• w is the driving frequency
• F0 is the magnitude of the applied force
• We take c 0 to start with

Displacement
x
k
FF0coswt
M
c
21
Equations of motion

• Solution is the sum of homogenous and particular
  solution
• The particular solution assumes form of forcing
  function (physically the input wins)

22
Substitute particular solution into the equation
of motion
Thus the particular solution has the form
23
Add particular and homogeneous solutions to get
general solution
24
Apply the initial conditions to evaluate the
constants
25
Comparison of free and forced response

• Sum of two harmonic terms of different frequency
• Free response has amplitude and phase effected by
  forcing function
• Our solution is not defined for wn w because it
  produces division by 0.
• If forcing frequency is close to natural
  frequency the amplitude of particular solution is
  very large

26
Response for m100 kg, k1000 N/m, F100 N, w
wn 5 v00.1m/s and x0 -0.02 m.
0.05
0
Displacement (x)
-0.05
0
2
4
6
8
10
Time (sec)
Note the obvious presence of two harmonic signals
Go to code demo
27
What happens when w is near wn?
When the drive frequency and natural frequency
are close a beating phenomena occurs
1
0.5
0
Displacement (x)
Larger amplitude
-0.5
-1
0
5
10
15
20
25
30
Time (sec)
28
What happens when w is wn?
When the drive frequency and natural frequency
are the same the amplitude of the vibration grows
without bounds. This is known as a resonance
condition
29
Example 2.1.1 Compute and plot the response for
m10 kg, k1000 N/m, x00,v00.2 m/s, F23 N,
w2wn.
30
Example 2.1.2 Given zero initial conditions a
harmonic input of 10 Hz with 20 N magnitude and
k 2000 N/m, and measured response amplitude of
0.1m, compute the mass of the system.