Aucun titre de diapositive - PowerPoint PPT Presentation
1 / 1
Title:
Aucun titre de diapositive
Description:
Title: Aucun titre de diapositive Author: SAILLE Last modified by: LUG Created Date: 9/7/1999 7:58:11 AM Document presentation format: Personnalis – PowerPoint PPT presentation
Number of Views:28
Avg rating:3.0/5.0
Title: Aucun titre de diapositive
1
A METHODOLOGY FOR EVALUATING THE PRECISION OF
FIXED-POINT SYSTEMS
.
Abstract The minimization of cost, power
consumption and time to market of DSP
applications requires the development of
methodologies for the automatic implementation of
floating-point algorithms in fixed-point
architectures. In this paper, a new methodology
for evaluating the quality of an implementation
through the automatic determination of the Signal
to Quantization Noise Ratio (SQNR) is under
consideration. The modelization of the system at
the quantization noise level and the expression
of the output noise power have been detailed for
linear systems. Then, the different phases of the
methodology are explained and the ability of our
approach for computing the SQNR efficiently is
shown.
- Embedded Digital Signal Processing (DSP) systems
- Specification with floating-point data types
- Implementation in fixed-point architectures
- Precision evaluation based on simulation
Coster98, Keding01, Kim98 - Long simulation time Coster98
- Optimization process requires multiple
simulations Sung95 - Definition of a new methodology based on an
analytical approach
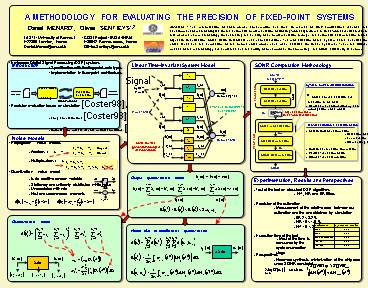
Linear Time-Invariant System Model
SQNR Computation Methodology
Introduction
Source C algorithm
Signal
System noise model determination
DFG Generation
System Inputs
Fixed-point coding
Precision evaluation
- Noise source detection and insertion in the SFG
- Replacement of operators by their propagation
noise model
Floating-point description
Fixed-point specification
Front End
Output signal
SUIF
SFG Generation
Optimization
Error due to coefficient quantization
Input noises
Signal Flow Graph fixed-point specifications
Gs
Noise modelization
- SFG to DAG transformation
- Detection of cycles in the SFG
- Enumeration of the cycles
- Dismantling of the cycles
- DAG linear function computation
- Partial T.F. determination
- Global T.F. determination
Transfer Function (T.F.) determination
Gsn
- Propagation noise models
- Addition z u v
- Multiplication z u ? v
- Quantization noise model
- bgi(n) additive random variable
- Stationary and uniformly distributed white noise
- Uncorrelated with y(n)
- First and second-order moments
Noise models
H(z) Determination
Output noise
Back End
Noise sources (generated during a cast operation)
GH
SQNR Determination
SQNR
Output quantization noise
Experimentation, Results and Perspectives
Q
- Test of the tool on classical DSP algorithms
- FFT, FIR and IIR filters
- Precision of the estimation
- Measurement of the relative error between our
estimation and the one obtained by simulation - IIR 2 lt 8.2
- FIR 16 lt 1.5
- FFT 16 lt 2.3
- Execution time of the tool
- Perspectives
- Hardware synthesis minimization of the chip
area under SQNR constraint
Quantization noise
Noise due to coefficient quantization
- Most of the time is consumed by the cycle
enumeration stage