PowerPoint-Pr PowerPoint PPT Presentation
1 / 38
Title: PowerPoint-Pr
1
- Spatial estimation of geotechnical parameters for
numerical tunneling simulations and TBM
performance models
George Exadaktylos George Xiroudakis TUC,
Laboratory of Mining Engineering Design,
Greece Maria Stavropoulou UOA, Greece
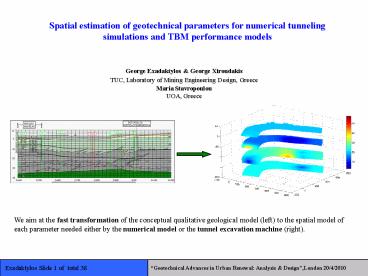
We aim at the fast transformation of the
conceptual qualitative geological model (left) to
the spatial model of each parameter needed either
by the numerical model or the tunnel excavation
machine (right).
2
Introduction (motivations proposed approach)
- No clear procedures on how geological-geomechanica
l data needed for the determination of ground
behavior is transferred into input data for 3D
numerical tools. Dispersed exploration, lab
testing, monitoring and other data of a given
project. Also, not optimized exploration
sampling designs. - Note In the majority of models, soil or rock
parameters data are averaged over very large
volumes (geological units or sections) and
assigned uniformly to each building brick
(element) of the model. - Experience (geological geotechnical) from
previous projects is not usually exploited. - Spatial uncertainty and risk that seriously
affecting project development decisions, are
frequently not considered properly.
3
Introduction (motivations proposed approach)
contd
- Concerns of excavation machines developers (i.e.
rock soil TBMs, Roadheaders) regarding the
spatial distribution of geomaterials strength
and wear parameters inside the geological domain
(e.g. for optimization of machine head, cutting
tools, operational parameters etc). Also, inverse
problem of characterization of geomaterials from
logged machine data (see fig. below).
4
Proposed tunnel design procedure
- INPUT DISCRETIZED SOLID GEOLOGICAL MODEL (CAD
MIDAS solid modeling from geological sections,
boreholes, geophysics, topographical map etc)
do i1,n
LAB web-driven DATABASE WITH CONSTITUTIVE MODELS
LIBRARY
REALIZATION OF RANDOM FIELD OF MATERIAL
PARAMETERS VIA KRIGSTAT CODE
- 3D GEOSTATISTICAL-GROUND MODEL
IN SITU STRESSES, BCs, GROUNDWATER
INPUT TO FE/BE/FD MODEL
INPUT TO TBM/RH PERFORMANCE MODEL (analytical,
fast)
TUNNEL ALIGNMENT, SUPPORT MEASURES- SPECS FOR
BORING MACHINES- OPERATIONAL PARAMETERS- DESIRED
SCHEDULES
continue
RUN DETERMINISTIC FE/BE/FD TUNNEL MODEL
RUN TBM/RH EXCAVATION MODEL CUTTING-CALC CODE
FEEDBACK (Back-analysis of TBM/RH logs,
convergence, subsidence etc)
POST-PROCESSING (Statistics, Residual Risks,
Cost, Advance rate etc)
Fig. 1. Non-intrusive modeling scheme
5
Descriptive statistics module of KRIGSTAT code
6
Geostatistical approachLocal estimation
accounting for secondary information
Stochastic Processes loosely speaking systems
that evolve probabilistically with time. The
concept of Random Function (RF) For each xi
there is assigned a RV. The theory of stochastic
processes and RFs has been in use for a
relatively long time to solve problems of
interpolation or filtering.
- Intrinsic hypothesis the variance of the
increment of two random variables corresponding
to two locations inside a given geological body
depends only on the vector h separating these two
points
The function ?(h) is called semivariogram
function and may be anisotropic and periodical.
7
The semivariogram is the simplest way to relate
uncertainty with distance from an observation.
No spatial dependence
From Chiles JP, Delfiner P (1999) Geostatistics
Modeling Spatial Uncertainty. John Wiley
Sons, New York.
8
Kriging estimation Equations in Kriging module
of KRIGSTAT
The expected value of variable z
i.e. z may stand for RMR - at location x0 can be
interpolated as follows
Ordinary Kriging (OK) determines the weights
(i1,,m) by solving the following system of
equations (mnumber of hard data)
System of (m1) eqns with (m1)
unknowns (ßLagrange multiplier)
Minimization of the variance of estimation
error (BLUES)
Estimation error or uncertainty
16 risk estimation
9
Geostatistical estimation Simulation Annealing
(SA) module of KRIGSTAT
SA Spatially consistent Monte Carlo simulation
method
The initial picture is modified by swapping the
values in pairs of grid nodes (concept from Solid
State Physics annealing process). A swap is
accepted if the objective (energy) function OF
(average squared difference between the
experimental and the model semivariogram) has
been decreased.
(lt1) rate of temperature decrease
10
Modeling methodology
First, distinct statistical and geotechnical
populations should be defined in order to group
data with similar characteristics into subsets,
called geotechnical units (i.e statistically
homogeneous regions).
Based on geological criteria and hard data
(boreholes, geophysics etc)
11
Discretized Solid Geological Models (DSGM) with
KRIGSTAT-MIDAS
L9, Mas-Blau (EPB tunnel in soft soil)
L9, Singuerlin-Esglesias (TBM tunnel in hard rock)
Koralm (alpine tunnel in soft rock)
References MIDAS GTSII Geotechnical and Tunnel
analysis System, MIDASoft Inc. (1989-2006),
http//www.midas-diana.com
L9, La Salut-Liefa (EPB tunnel in soil)
12
Modeling methodology contd
Second, proceed with geostatistical interpolation
of the parameter of interest inside each
geological unit and in the tube, using KRIGSTAT
at the nodes already created with MIDAS-GTS. One
may use either Kriging or SA. Before this, for
both approaches the semivariogram model should be
fitted on the experimental data.
13
1st case study Singuerlin-Esglesias L9 TBM
tunnel in weathered granite
RMR sampling
RMR sampling locations in boreholes
Conceptual geological model
KRIGSTAT Stratigraphy of layers
Solid geological model (MIDAS-GTS)
Finite Element model (MIDAS-GTS)
14
RMR semivariogram
Kriging RMR model
15
Anisotropic semivariogram of GR1
RMR simulated and theoretical histograms
SA estimation of RMR in GR1 formation
Kriging estimation of RMR in GR1 formation
16
Special upscaling procedure for rocks (Linking
RMR with rock mass properties)
Exadaktylos G. and Stavropoulou M., A Specific
Upscaling Theory of Rock Mass Parameters
Exhibiting Spatial Variability Analytical
relations and computational scheme, International
Journal of Rock Mechanics and Mining Sciences, 45
(2008) 11021125.
Rock mass Elasticity Strength
Lab scale Elasticity Strength (RMDB)
Physical degradation
Size effect
Hypothesis A In a first approximation upscaling
due to degradation effect of joints may be based
on the constant scalar or vector damage parameter
D for the anisotropic case of joint induced
anisotropy of the rock mass (n is the unit normal
vector of the plane of interest).
Hypothesis B Strain Equivalence Principle
(Lemaitre, 1992), namely Any strain
constitutive equation for a damaged geomaterial
may be derived in the same way for an intact
geomaterial except that the usual stress is
replaced by the effective stress.
17
Hypothesis C The function linking damage D with
rock mass quality described with RMR (or Q or
GSI) must have a sigmoidal shape resembling a
cumulative probability density function giving D
in the range of 0 to 1 for RMR or GSI varying
between 100 to 0 or for Q varying from 1000 to
0.001, respectively.
Size effect
Calibration of the parameters of the Lorentzian
curve on in situ test data presented by Hoek and
Brown (1997)
Verification of the Lorentzian law with
additional data on deformability of rock masses
presented by Hoek and Diederichs (2006)
18
Upscaling relations for the 7-parameter
linear-elastic, perfectly-plastic HMCM
Size effect
Size effect of UCS (left) UTS (right) of rocks
19
3D GroundTunnel Models (KRIGSTAT/MIDAS)
The rest of ground parameters derived from RMR
lab data in a similar fashion based on the
special upscaling theory.
20
TBM Roadheader performance models
- The new CUTTING_CALC software for excavation
performance analysis optimization of TBMs. The
concept of transformation of geological model
into machine performance model.
CUTTING_CALC code may be add-on of tunneling
machines or for work nearly real-time in the
office.
GUI of the algorithm
21
RMR estimations along the tunnel from the TBM
data by virtue of empirical hyperbolic
relationship during TBM advance are combined with
the borehole data in order to upgrade the initial
geotechnical model (RMR model) derived from the
Kriging analysis of borehole data.
Boreholes only
Upgraded RMR data (boreholes TBM)
Boreholes and TBM logging Reduction of kriging
error
Exadaktylos G., M. Stavropoulou, G. Xiroudakis,
M. de Broissia and H. Schwarz, (2008) A spatial
estimation model for continuous rock mass
characterization from the specific energy of a
TBM, Rock Mechanics Rock Engineering, 41
797834, Springer.
22
2nd case study Mas-Blau L9 EPB tunnel in soft
alluvial deposits
Mas-Blau tunnel will run in the alluvial
Quaternary deposits of Llobregat river, composed
by intercalated strata of sands, gravel, silts
and clay.
Generation of 3D terrain model
Point data from boreholes are interpolated with
Kriging and feeded to MIDAS for modeling the
surface of each geological formation.
23
Mas-Blau models KRIGSTAT-MIDAS
Geological Model
Tube geology
Discretized solid geological model
24
NSPT variogram (KRIGSTAT)
NSPT kriging Model on nodes created by MIDAS
25
EPB boring performance at Mas-Blau
EPB (S-461)
Traces of knives, with S10 cm
SE2 (MPa) Kriging model
Specific Energy of soil cutting
Knives design
26
(No Transcript)
27
Plasticity slip-line analytical model for soil
cutting
28
Back-analysis of SE logged data for estimation of
cohesion
29
3rd case study La Salut-Liefa L9 EPB tunnel in
hard tertiary alluvial formation
S-221
Note The gravel QB2g was not found in crown of
the tunnel. The profile is an interpretation of
boreholes and georadar. A re-interpretation of
georadar situated the QB2g about 2 m higher,
clearly outside the tunnel section.
30
Finite Element Model
31
UCS along chainage from back-analysis of SE data
based on the slip-line model
32
3rd case study Koralm alpine tunnel in soft rock
(molassic) formations
3D view of the Koralm alpine tunnel with the
region of interest encircled
Geological model of the tunnel Paierdorf
Solid geological model of the particular domain
of interest (MIDAS)
33
Homogenization method Derive the spatial
distribution of volume fraction n of silt, sand
and sandstone along tunnel using KRIGSTAT and
then derive the effective elastic and strength
properties (P) of the homogenized material using
Mixtures theory and assuming mean values derived
from statistics.
Example of the geology mapped at the face that is
conceived as a mixture
Experimental model variograms of siltstone
concentration () exhibiting a hole effect
(periodicity)
Spatial model of siltstones specific volume ()
at every 5 m along the 500 m tunnel section
Example statistics of mechanical parameters of
siltstone
34
Example Validation of siltstones Kriging model
Upscaling method Assuming the hyperbolic
Mohr-Coulomb model and a perfectly-plastic
behavior the 16 properties of the homogenized
geomaterial are derived assuming a size effect of
strength properties (50 reduction) but not on
elastic properties.
Spatial distribution of cohesion (c) and elastic
modulus (E) along tunnel
35
Initial discretized geological model (MIDAS)
MIDAS-KRIGSTAT ground tube models
36
BEFE (Beer et al., 2009)
Rock parameters along the tunnel
Vertical displacements on the tunnel roof
(comparison with the measurements)
Deformed shape and contour of displacement
results
position 213m behind the exploration shaft
Paierdorf
37
Concluding remarks
Modeling and visualization of the geology and
geotechnical parameters, as well as the
performance of tunneling machines (boring TBMs
and excavation RHs) are the most important tasks
in tunneling design and construction. The
design process should take into account the risk
associated with the rock or soil quality, and the
performance of the excavation machine. Also the
best sampling strategy should be found. In this
perspective there have been developed among
others
1. The new Geostatistics package KRIGSTAT for 1D,
2D 3D spatial analysis and interpolation
through kriging (or co-kriging) or simulation of
stratigraphical or geotechnical parameters of
each geological formation with evaluation of
uncertainty of predictions. This software could
be combined with the concept of DSGM developed
to feed directly numerical simulation tools like
MIDAS Risk Analysis software. 2. The new
CUTTING_CALC software for excavation performance
analysis optimization of TBMs. The concept of
transformation of geological model into
machine performance model.
38
Thank you for your kind attention!!.. If you need
further information or you would like to make
comments or seek cooperation for research and
applications do not hesitate to contact
us exadakty_at_mred.tuc.gr mstavrop_at_geol.uoa.gr
Acknowledgements
Technology Innovation in Underground Construction
MIDAS-GTS TNO DIANA BV