Les ensembles de nombres

1
Les ensembles de nombres
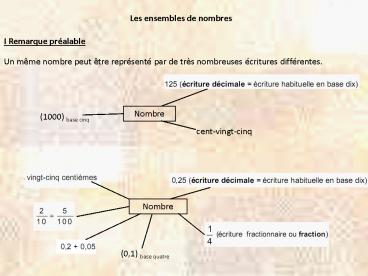
I Remarque préalable
Un même nombre peut être représenté par de très
nombreuses écritures différentes.
Nombre
(1000) base cinq
cent-vingt-cinq
Nombre
(0,1) base quatre
2
II Les différents ensembles de nombres
Ensemble des nombres réels
2,536
- 6,38
- 7
0
5
2 7
Ensemble des nombres rationnels (peuvent être
écrits avec a et b entiers )
Ensemble des entiers naturels
- 345
Ensemble des entiers relatifs
Ensemble des nombres décimaux (admettent une
représentation décimale finie)
D
3




Peuvent être représentés par une écriture
décimale sans virgule.
Nombres entiers
Peuvent être représentés par une écriture
décimale finie.
Nombres décimaux (dont nombres entiers)
(Remarque tout nombre décimal admet deux
écritures décimales car 3 2,9 237,25
237,249 )
Nombres rationnels (dont nombres décimaux)
Ceux qui admettent une représentation décimale
finie sont les décimaux les autres admettent
une représentation décimale infinie périodique
(Exemple - 27, 52315)
Nombres réels (dont nombres rationnels)
Pour ceux qui sont rationnels , voir ligne du
dessus. Les autres (appelés irrationnels)
admettent une écriture décimale infinie non
périodique.
4
III Nombres décimaux différentes approches
dune même notion
1) Un nombre décimal est un nombre qui PEUT être
représenté par une écriture décimale finie.
2) Un nombre décimal est un nombre qui PEUT être
représenté par une fraction du type
avec a et n entiers. Exemple
3) Un nombre décimal est un nombre qui PEUT être
représenté par une fraction IRREDUCTIBLE
telle que la décomposition en facteurs premiers
du dénominateur d ne comporte que des 2 ou des
5 (donc soit que des 2, soit que de 5 soit des 2
et des 5).
5
Exemples
D. Pernoux http//dpernoux.net